一鼻子闻出逻辑谬误

100多年前,人们普遍认为记忆力不好或者不用功学习就容易忘记,但艾宾浩斯画了一根曲线告诉人们:学了忘,忘了学,学了之后还会忘,但相隔四段以上时间之后,普遍比单纯记忆一次的效果要好太多。
这就是著名的艾宾浩斯遗忘曲线(Forgetting curve)。
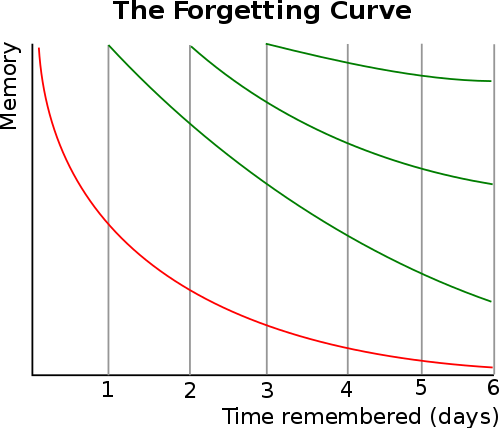
100多年后,这条曲线几乎成为全世界考生的圣经,似乎这根曲线的高度等于他们未来人生阶层的高度,所以他们像西西弗斯那样,夜以继日地把巨石球推上山。
考生普遍不太会去记忆那些长期技能,比如逻辑,因为99%以上的专业没有逻辑课,而且就算有,也是光秃秃的数理逻辑,和日常生活不太沾边的抽象思考,看了让人肝颤。
到最后大多数人失去受用一生的判断能力,原因居然是不知道判断能力是一种能力,而且是一种不难的能力,你需要简单地了解到他,并接受刻意训练。
通过过去的16篇文章,我们已经了解了16种谬误,这些谬误都属于形式谬误——推理中有逻辑结构缺陷,使得推理在逻辑上无效。
学过之前专栏文章的读者朋友能理解:不是所有的形式谬误都会推导出错误的结论,但形式谬误的推导过程都有逻辑问题,找出问题,才能接近本质。
形式逻辑主要分为三大类,好巧,这三大类我们都学过,所以,复习吧~
1、命题逻辑谬误
我们不是哲学或逻辑学专业的,所以把『命题』理解为『判断』或者『推理』,那么更有助于我们理解逻辑。
命题逻辑是把命题看做不可分割的整体,对多个命题做真假值运算,主要运算包括:非、联言(且)、选言(或)、蕴含(若)、等值(当且仅当)。违反命题逻辑运算规则的,都是命题逻辑谬误。
1)肯定后件
以前提中的结论作为条件,推导出条件必然成立。
如果车没油,那么车跑不起来。
现在,车没跑起来,
所以,车一定没油。
所有骑士都穿盔甲。
那个人穿了盔甲,
所以,那个人是骑士。
『若P则Q』为真,且Q为真,推得P为真。
2)否定前件
否定前提中的条件,以此否定原结论。
如果锯子响了,就会有木屑碎末。
现在,锯子没响,
所以,一定没末。
如果一早路面湿了,那么昨晚就下过雨。
今天一早路面没湿。
所以,昨晚没下雨。
『若P则Q』为真,且P为假,推得Q为假。
3)肯定选言
前提有两个选言支,前提明确选言支合并结果为真,肯定其中一个,而否定另一个。
杂志封面人物必须长得漂亮,或者是名人才行。
这个月的封面人物是一位名人,
所以,这位名人一定不美。
要么鱼死,要么网破,
现在鱼死了,
所以,网没破。
『P或Q』为真,且P为真,推得Q为假。
4)否定联言
前提有两个联言支,前提明确联言支合并结果为假,否定其中一个,而肯定另一个。
你不能既在深圳,又在上海。
现在,你不在深圳。
所以,你现在在上海。
做人不能既当又立,
我没当,
所以,我一定立了。
『P且Q』不为真,且P不为真,推得Q为真。
以上四种谬误为命题逻辑谬误,推理过程存在硬伤,需要我们多加刻意练习,练到不经大脑,一眼识别,一耳拎清,一鼻子闻出来。
2、量化词逻辑谬误
这是对命题逻辑的扩充,引入量化词运算子『对于所有的……』、『存在……』,误用量化词相关运算规则,就会构成量化词逻辑谬误,有以下五种:
1)无端对立
把特称肯定句与特称否定句互转。
你店里有些牛奶没过期,
所以,你店里有些牛奶过期了。
有些蚂蚁不是人,
所以,有些蚂蚁是人。
特称肯定句往往给接收者理解上产生这样的暗示:『有些是,那么就有些不是』。才会批量生产神逻辑。
2)非法换位
亚里士多德老师敲黑板:请复习A、E、I、O的对立四边形:
| 类型 | 代号 | 形式 | 举例 | 能否换位 |
|---|---|---|---|---|
| 全称肯定 | A(SaP) | 所有S是P | 所有猫都有四条腿 | 否 |
| 全称否定 | E(SeP) | 没有S是P | 所有猫都不是狗 | 能 |
| 特称肯定 | I(SiP) | 有些S不是P | 有些狗是宠物 | 能 |
| 特称否定 | O(SoP) | 有些S不是P | 有些猫不是宠物 | 否 |
只有E和I两种情况下可以换位:
- E(全称否定)合法换位
鲸鱼都不是鱼,
所以,鱼都不是鲸鱼。
- I(特称肯定)合法换位
有些苹果是水果,
所以,有些水果是苹果。
A和O则不能:
- A(全称肯定)非法换位:
所有喜剧演员都是有趣的人,
所以,所有有趣的人都是喜剧演员。
- O(特称否定)非法换位:
有些马路铺沥青,
所以,有些马路没铺沥青。
3)不当换质换位
换质,就是转换是与非:把『是』换成『非』,或者把『非』换成『是』。
换位,就是对调前后件:把『前件』换成『后件』,『前件』相当于『如果』之后的内容;『后件』相当于『那么』之后的内容。
如果换质换位过程中,出了逻辑问题,那就是不当换质换位,比如:
真金不怕火炼,
所以,不真的金才怕火炼。
另外,肯定后件也是一种不当换质换位,即所谓的换位不换质。
换质换位的一般程序是:先换质,后换位。
真金不怕火炼
先换质:真金不是怕或炼的
再换位:怕或炼的不是真金
4)存在性谬误
错误假设某些集合非空
所有打人者都将被起诉,
因此,被起诉的人中有些是打人者。
每个独角兽额头上只有一只角,
所以,有些独角兽额头上只有一只角。
从『对于所有的X』推理出『一定存在X』,这是存在性谬误的核心。
5)量化词对调
每个人都爱着一些人,
所以,有些人是每个人都爱的。
- 注意反向量化词对调的情形,这是正确的:
有一个女人,是隔壁一家所有孩子的母亲,
所以,对于隔壁一家的所有孩子来说,都有一个女人作为母亲。
把『对于所有的…存在…』对调为『存在…对于所有的…』
形式谬误包括命题逻辑谬误、量化词逻辑谬误和三段论逻辑谬误,今天我们复习了前两者,明天我们复习三段论,锻炼脑肌,脑不能停。