First Princeton Paperback printing, 1971
Second printing, 1973
普林斯顿大学平装本第一次印刷，1971 年
第二次印刷，1973 年
First Princeton Science Library Edition, 1988
普林斯顿科学图书馆第一版，1988 年
Expanded Princeton Science Library Edition,
with a new foreword by John H. Conway, 2004
普林斯顿科学图书馆扩大版，
，有 John H·Conway 的新前言，2004 年
Library of Congress Control Number 2004100613
美国国会图书馆控制号 2004100613
ISBN-13: 978-0-691-11966-3 (pbk.)
ISBN-13: 978-0-691-11966-3（pbk.）
ISBN-10: 0-691-11966-X (pbk.)
ISBN-10: 0-691-11966-X（pbk.）
British Library Cataloging-in-Publication Data is available
大英图书馆编目出版数据可查
Printed on acid-free paper. ∞
用无酸纸印刷。∞
psl.princeton.edu
psl.princeton.edu
Printed in the United States of America
在美国印刷
3 5 7 9 10 8 6 4
3 5 7 9 10 8 6 4
A great discovery solves a great problem but there is a grain of discovery in the solution of any problem. Your problem may be modest; but if it challenges your curiosity and brings into play your inventive faculties, and if you solve it by your own means, you may experience the tension and enjoy the triumph of discovery. Such experiences at a susceptible age may create a taste for mental work and leave their imprint on mind and character for a lifetime.
一个伟大的发现可以解决一个伟大的问题，但在解决任何问题的过程中都有一粒发现。你的问题可能不大，但如果它挑战你的好奇心，发挥你的发明能力，如果你用自己的方法解决它，你可能会体验到紧张，享受发现的胜利。在易受影响的年龄，这样的经历可能会培养出对脑力劳动的兴趣，并在思想和性格上留下终生的烙印。
Thus, a teacher of mathematics has a great opportunity. If he fills his allotted time with drilling his students in routine operations he kills their interest, hampers their intellectual development, and misuses his opportunity. But if he challenges the curiosity of his students by setting them problems proportionate to their knowledge, and helps them to solve their problems with stimulating questions, he may give them a taste for, and some means of, independent thinking.
因此，数学教师有一个很好的机会。如果他把分配给他的时间都用在钻研学生的常规操作上，就会扼杀他们的兴趣，阻碍他们的智力发展，并滥用他的机会。但是，如果他通过给学生设置与他们的知识相称的问题来挑战他们的好奇心，并通过刺激性的问题帮助他们解决问题，他就可以让他们尝到独立思考的滋味，并掌握一些方法。
Also a student whose college curriculum includes some mathematics has a singular opportunity. This opportunity is lost, of course, if he regards mathematics as a subject in which he has to earn so and so much credit and which he should forget after the final examination as quickly as possible. The opportunity may be lost even if the student has some natural talent for mathematics because he, as everybody else, must discover his talents and tastes; he cannot know that he likes raspberry pie if he has never tasted raspberry pie. He may manage to find out, however, that a mathematics problem may be as much fun as a crossword puzzle, or that vigorous mental work may be an exercise as desirable as a fast game of tennis. Having tasted the pleasure in mathematics he will not forget it easily and then there is a good chance that mathematics will become something for him: a hobby, or a tool of his profession, or his profession, or a great ambition.
The author remembers the time when he was a student himself, a somewhat ambitious student, eager to understand a little mathematics and physics. He listened to lectures, read books, tried to take in the solutions and facts presented, but there was a question that disturbed him again and again: “Yes, the solution seems to work, it appears to be correct; but how is it possible to invent such a solution? Yes, this experiment seems to work, this appears to be a fact; but how can people discover such facts? And how could I invent or discover such things by myself?” Today the author is teaching mathematics in a university; he thinks or hopes that some of his more eager students ask similar questions and he tries to satisfy their curiosity. Trying to understand not only the solution of this or that problem but also the motives and procedures of the solution, and trying to explain these motives and procedures to others, he was finally led to write the present book. He hopes that it will be useful to teachers who wish to develop their students’ ability to solve problems, and to students who are keen on developing their own abilities.
作者还记得他自己还是学生的时候，一个有点野心的学生，渴望了解一点数学和物理学。他听讲座，看书，试图接受提出的解决方案和事实，但有一个问题一次又一次地困扰着他。“是的，这个解决方案似乎是有效的，它似乎是正确的；但怎么可能发明这样的解决方案？是的，这个实验似乎是有效的，这似乎是一个事实；但人们如何能发现这样的事实？我又怎么可能自己发明或发现这样的事情呢？” 今天，作者在大学里教数学；他认为或希望他的一些比较热心的学生问类似的问题，他试图满足他们的好奇心。他不仅试图了解这个或那个问题的解决方法，还试图了解解决问题的动机和程序，并试图向别人解释这些动机和程序，最终促使他写下了这本书。他希望这本书对希望培养学生解决问题的能力的教师和热衷于培养自己能力的学生有所帮助。
Although the present book pays special attention to the requirements of students and teachers of mathematics, it should interest anybody concerned with the ways and means of invention and discovery. Such interest may be more widespread than one would assume without reflection. The space devoted by popular newspapers and magazines to crossword puzzles and other riddles seems to show that people spend some time in solving unpractical problems. Behind the desire to solve this or that problem that confers no material advantage, there may be a deeper curiosity, a desire to understand the ways and means, the motives and procedures, of solution.
The following pages are written somewhat concisely, but as simply as possible, and are based on a long and serious study of methods of solution. This sort of study, called heuristic by some writers, is not in fashion nowadays but has a long past and, perhaps, some future.
以下几页写得有些简明，但尽可能简单，是基于对解决方法的长期和认真研究。这种研究被一些作家称为启发式研究，在今天并不流行，但却有着悠久的历史，或许还有一些未来。
Studying the methods of solving problems, we perceive another face of mathematics. Yes, mathematics has two faces; it is the rigorous science of Euclid but it is also something else. Mathematics presented in the Euclidean way appears as a systematic, deductive science; but mathematics in the making appears as an experimental, inductive science. Both aspects are as old as the science of mathematics itself. But the second aspect is new in one respect; mathematics “in statu nascendi,” in the process of being invented, has never before been presented in quite this manner to the student, or to the teacher himself, or to the general public.
研究解决问题的方法，我们可以感知到数学的另一面。是的，数学有两张面孔；它是欧几里得的严格科学，但也是另一种东西。以欧几里得方式呈现的数学似乎是一门系统的、演绎的科学；但正在形成的数学则是一门实验的、归纳的科学。这两个方面都与数学科学本身一样古老。但第二个方面在一个方面是新的；“新生状态” 的数学，在被发明的过程中，从来没有以这种方式呈现给学生，或教师本人，或公众。
The subject of heuristic has manifold connections; mathematicians, logicians, psychologists, educationalists, even philosophers may claim various parts of it as belonging to their special domains. The author, well aware of the possibility of criticism from opposite quarters and keenly conscious of his limitations, has one claim to make: he has some experience in solving problems and in teaching mathematics on various levels.
启发式的主题有多方面的联系；数学家、逻辑学家、心理学家、教育学家、甚至哲学家都可以声称它的各个部分属于他们的特殊领域。作者深知来自相反方面的批评的可能性，并敏锐地意识到自己的局限性，他有一个要求：他在解决问题和在不同层次的数学教学方面有一些经验。
The subject is more fully dealt with in a more extensive book by the author which is on the way to completion.
这个问题在作者的一本更广泛的书中得到了更充分的论述，该书即将完成。
Stanford University, August 1, 1944
斯坦福大学，1944 年 8 月 1 日
I am glad to say that I have now succeeded in fulfilling, at least in part, a promise given in the preface to the first printing: The two volumes Induction and Analogy in Mathematics and Patterns of Plausible Inference which constitute my recent work Mathematics and Plausible Reasoning continue the line of thinking begun in How to Solve It.
我很高兴地说，我现在已经成功地履行了，至少是部分地履行了在第一次印刷的序言中所作的承诺。两卷《数学中的归纳与类比》和《合理推理的模式》构成了我最近的作品《数学与合理推理》，它们延续了《如何解决》中开始的思路。
Zurich, August 30, 1954
苏黎世，1954 年 8 月 30 日
The present second edition adds, besides a few minor improvements, a new fourth part, “Problems, Hints, Solutions.”
目前的第二版除了一些小的改进之外，还增加了新的第四部分，“问题、提示、解决方案”。
As this edition was being prepared for print, a study appeared (Educational Testing Service, Princeton, N.J.; cf. Time, June 18, 1956) which seems to have formulated a few pertinent observations—they are not new to the people in the know, but it was high time to formulate them for the general public—: “. . . mathematics has the dubious honor of being the least popular subject in the curriculum . . . Future teachers pass through the elementary schools learning to detest mathematics . . . They return to the elementary school to teach a new generation to detest it.”
在本版准备印刷时，出现了一项研究（教育测试服务，普林斯顿，新泽西；参见《时代》杂志，1956 年 6 月 18 日），它似乎提出了一些相关的意见 —— 对知情者来说，这些意见并不新鲜，但现在是为大众提出这些意见的时候了 —— 。“…… 数学是课程中最不受欢迎的科目，这是一个令人怀疑的荣誉。未来的教师通过小学的学习，厌恶数学…… 他们回到小学是为了教导新一代的人厌恶它。”
I hope that the present edition, designed for wider diffusion, will convince some of its readers that mathematics, besides being a necessary avenue to engineering jobs and scientific knowledge, may be fun and may also open up a vista of mental activity on the highest level.
我希望本版旨在更广泛地传播，能使一些读者相信，数学除了是通向工程工作和科学知识的必要途径外，还可能是一种乐趣，也可能在最高层次上开辟出精神活动的视野。
|
|
UNDERSTANDING THE PROBLEM |
|
First. You have to understand the problem. |
What is the unknown? What are the data? What is the condition? Is it possible to satisfy the condition? Is the condition sufficient to determine the unknown? Or is it insufficient? Or redundant? Or contradictory? Draw a figure. Introduce suitable notation. Separate the various parts of the condition. Can you write them down? |
|
|
了解问题 |
|
首先 你必须 理解 这个问题。 |
未知数是什么？数据是什么？条件是什么？ 是否有可能满足该条件？该条件是否足以确定未知数？还是不充分？或者是多余的？或者是矛盾的？ 画一个图形。引入适当的符号。 把条件的各个部分分开。你能把它们写下来吗？ |
|
|
CARRYING OUT THE PLAN |
|
Third. Carry out your plan. |
Carrying out your plan of the solution, check each step. Can you see clearly that the step is correct? Can you prove that it is correct? |
|
|
执行计划 |
|
第三。 执行你的计划。 |
执行你的解决方案计划，检查每个步骤。你能清楚地看到这个步骤是正确的吗？你能证明它是正确的吗？ |
How to Solve It is a wonderful book! This I realized when I first read right through it as a student many years ago, but it has taken me a long time to appreciate just how wonderful it is. Why is that? One part of the answer is that the book is unique. In all my years as a student and teacher, I have never seen another that lives up to George Polya’s title by teaching you how to go about solving problems. A. H. Schoenfeld correctly described its importance in his 1987 article “Polya, Problem Solving, and Education” in Mathematics Magazine: “For mathematics education and the world of problem solving it marked a line of demarcation between two eras, problem solving before and after Polya.”
如何解决》是一本精彩的书!许多年前我作为学生第一次通读时就意识到了这一点，但我花了很长时间才体会到它有多么美妙。为什么这么说呢？答案的一部分是这本书是独一无二的。在我当学生和老师的这些年里，我从未见过另一本能达到乔治·波利亚的标题，教你如何去解决问题的书。A·H. Schoenfeld 在他 1987 年发表在《数学杂志》上的文章《波利亚、问题解决和教育》中正确描述了它的重要性。“对于数学教育和问题解决的世界来说，它标志着两个时代的分界线，即波利亚之前和之后的问题解决。”
It is one of the most successful mathematics books ever written, having sold over a million copies and been translated into seventeen languages since it first appeared in 1945. Polya later wrote two more books about the art of doing mathematics, Mathematics and Plausible Reasoning (1954) and Mathematical Discovery (two volumes, 1962 and 1965).
这本书是有史以来最成功的数学书之一，自 1945 年首次出版以来，销量超过 100 万册，被翻译成 17 种语言。波利亚后来又写了两本关于做数学的艺术的书：《数学与合理推理》（1954）和《数学发现》（两卷，1962 和 1965）。
The book’s title makes it seem that it is directed only toward students, but in fact it is addressed just as much to their teachers. Indeed, as Polya remarks in his introduction, the first part of the book takes the teacher’s viewpoint more often than the student’s.
这本书的标题让人觉得它只针对学生，但事实上，它也是针对教师的。事实上，正如波利亚在他的导言中所说的那样，本书的第一部分更多的是以教师的角度来看待问题，而不是以学生的角度。
Everybody gains that way. The student who reads the book on his own will find that overhearing Polya’s comments to his non-existent teacher can bring that desirable person into being, as an imaginary but very helpful figure leaning over one’s shoulder. This is what happened to me, and naturally I made heavy use of the remarks I’d found most important when I myself started teaching a few years later.
每个人都会有这样的收获。自己读这本书的学生会发现，无意中听到波利亚对他不存在的老师的评论，可以使那个理想的人出现，作为一个想象中的但非常有用的人物靠在自己的肩膀上。这就是发生在我身上的事情，自然而然地，当我自己在几年后开始教学时，我大量使用了我认为最重要的言论。
But it was some time before I read the book again, and when I did, I suddenly realized that it was even more valuable than I’d thought! Many of Polya’s remarks that hadn’t helped me as a student now made me a better teacher of those whose problems had differed from mine. Polya had met many more students than I had, and had obviously thought very hard about how to best help all of them learn mathematics. Perhaps his most important point is that learning must be active. As he said in a lecture on teaching, “Mathematics, you see, is not a spectator sport. To understand mathematics means to be able to do mathematics. And what does it mean [to be] doing mathematics? In the first place, it means to be able to solve mathematical problems.”
It is often said that to teach any subject well, one has to understand it “at least as well as one’s students do.” It is a paradoxical truth that to teach mathematics well, one must also know how to misunderstand it at least to the extent one’s students do! If a teacher’s statement can be parsed in two or more ways, it goes without saying that some students will understand it one way and others another, with results that can vary from the hilarious to the tragic. J. E. Littlewood gives two amusing examples of assumptions that can easily be made unconsciously and misleadingly. First, he remarks that the description of the coordinate axes (“Ox and Oy as in 2 dimensions, Oz vertical”) in Lamb’s book Mechanics is incorrect for him, since he always worked in an armchair with his feet up! Then, after asking how his reader would present the picture of a closed curve lying all on one side of its tangent, he states that there are four main schools (to left or right of vertical tangent, or above or below horizontal one) and that by lecturing without a figure, presuming that the curve was to the right of its vertical tangent, he had unwittingly made nonsense for the other three schools.
人们常说，要教好任何学科，就必须 “至少像学生一样理解它”。一个自相矛盾的事实是，要教好数学，还必须知道如何误解它，至少要达到学生的理解程度!如果一个教师的陈述可以用两种或更多的方式来解析，不言而喻，一些学生会用一种方式来理解，而另一些则用另一种方式来理解，其结果可能从热闹到悲惨。J·E. Littlewood 举了两个有趣的例子，说明很容易无意识地做出误导性的假设。首先，他说兰姆的《机械学》一书中对坐标轴的描述（“Ox和Oy是二维的，Oz垂直”）对他来说是不正确的，因为他总是在扶手椅上工作，脚是抬起来的！然后，他问他的读者如何看待这个问题。然后，在问了他的读者如何呈现一条封闭曲线全部位于其切线一侧的图片之后，他说有四个主要流派（在垂直切线的左边或右边，或在水平切线的上面或下面），在没有图形的情况下讲课，假定曲线在其垂直切线的右边，他不知不觉地让其他三个流派的人感到无趣。
I know of no better remedy for such presumptions than Polya’s counsel: before trying to solve a problem, the student should demonstrate his or her understanding of its statement, preferably to a real teacher, but in lieu of that, to an imagined one. Experienced mathematicians know that often the hardest part of researching a problem is understanding precisely what that problem says. They often follow Polya’s wise advice: “If you can’t solve a problem, then there is an easier problem you can’t solve: find it.”
Readers who learn from this book will also want to learn about its author’s life.1
从这本书中学习的读者也会想了解其作者的生活。1
George Polya was born György Pólya (he dropped the accents sometime later) on December 13, 1887, in Budapest, Hungary, to Jakab Pólya and his wife, the former Anna Deutsch. He was baptized into the Roman Catholic faith, to which Jakab, Anna, and their three previous children, Jenő, Ilona, and Flóra, had converted from Judaism in the previous year. Their fifth child, László, was born four years later.
乔治·波利亚于 1887 年 12 月 13 日出生在匈牙利布达佩斯的捷尔吉·波利亚（他后来放弃了这个口音），父亲是雅各布·波利亚和他的妻子，前妻是安娜·多伊奇。他接受了罗马天主教的洗礼，Jakab、Anna 和他们之前的三个孩子 Jenő、Ilona 和 Flóra 在前一年从犹太教皈依了天主教。他们的第五个孩子 László在四年后出生。
Jakab had changed his surname from Pollák to the more Hungarian-sounding Pólya five years before György was born, believing that this might help him obtain a university post, which he eventually did, but only shortly before his untimely death in 1897.
在捷尔吉出生前五年，雅卡布将他的姓氏从波拉克改成了听起来更像匈牙利语的波利亚，他认为这可能有助于他获得一个大学职位，他最终做到了，但只是在他 1897 年英年早逝前不久。
At the Dániel Berzsenyi Gymnasium, György studied Greek, Latin, and German, in addition to Hungarian. It is surprising to learn that there he was seemingly uninterested in mathematics, his work in geometry deemed merely “satisfactory” compared with his “outstanding” performance in literature, geography, and other subjects. His favorite subject, outside of literature, was biology.
在 Dániel Berzsenyi Gymnasium，捷尔吉除了学习匈牙利语外，还学习希腊语、拉丁语和德语。令人惊讶的是，他在那里似乎对数学不感兴趣，与他在文学、地理和其他科目的 “杰出” 表现相比，他在几何学方面的工作被认为只是 “令人满意”。在文学之外，他最喜欢的科目是生物。
He enrolled at the University of Budapest in 1905, initially studying law, which he soon dropped because he found it too boring. He then obtained the certification needed to teach Latin and Hungarian at a gymnasium, a certification that he never used but of which he remained proud. Eventually his professor, Bernát Alexander, advised him that to help his studies in philosophy, he should take some mathematics and physics courses. This was how he came to mathematics. Later, he joked that he “wasn’t good enough for physics, and was too good for philosophy—mathematics is in between.”
In Budapest he was taught physics by Eötvös and mathematics by Fejér and was awarded a doctorate after spending the academic year 1910–11 in Vienna, where he took some courses by Wirtinger and Mertens. He spent much of the next two years in Göttingen, where he met many more mathematicians—Klein, Caratheodory, Hilbert, Runge, Landau, Weyl, Hecke, Courant, and Toeplitz—and in 1914 visited Paris, where he became acquainted with Picard and Hadamard and learned that Hurwitz had arranged an appointment for him in Zürich. He accepted this position, writing later: “I went to Zürich in order to be near Hurwitz, and we were in close touch for about six years, from my arrival in Zürich in 1914 to his passing [in 1919]. I was very much impressed by him and edited his works.”
在布达佩斯，Eötvös 教他物理，Fejér 教他数学，1910-11 学年在维也纳学习了 Wirtinger 和 Mertens 的一些课程后被授予博士学位。在接下来的两年里，他在哥廷根度过了大部分时间，在那里他认识了更多的数学家 —— 克莱恩、卡拉特奥多里、希尔伯特、朗格、兰道、魏尔、赫克、库朗和托普利茨，并于 1914 年访问了巴黎，在那里他结识了皮卡尔和哈达玛，得知赫尔维茨在苏黎世为他安排了一个职位。他接受了这个职位，后来写道 “我去苏黎世是为了接近赫尔维茨，从我 1914 年到达苏黎世到他去世 1919 年，我们保持了大约六年的密切联系。我对他印象非常深刻，并编辑了他的作品”。
Of course, the First World War took place during this period. It initially had little effect on Polya, who had been declared unfit for service in the Hungarian army as the result of a soccer wound. But later when the army, more desperately needing recruits, demanded that he return to fight for his country, his strong pacifist views led him to refuse. As a consequence, he was unable to visit Hungary for many years, and in fact did not do so until 1967, fifty-four years after he left.
当然，第一次世界大战就发生在这一时期。它最初对波利亚影响不大，因为他因足球受伤而被宣布不适合在匈牙利军队中服役。但后来，当军队更迫切需要新兵时，要求他回去为国家作战，他强烈的和平主义观点使他拒绝了。因此，他多年来无法访问匈牙利，事实上直到 1967 年，即他离开后的 54 年才访问。
In the meantime, he had taken Swiss citizenship and married a Swiss girl, Stella Vera Weber, in 1918. Between 1918 and 1919, he published papers on a wide range of mathematical subjects, such as series, number theory, combinatorics, voting systems, astronomy, and probability. He was made an extraordinary professor at the Zürich ETH in 1920, and a few years later he and Gábor Szegő published their book Aufgaben und Lehrsatze aus der Analysis (“Problems and Theorems in Analysis”), described by G. L. Alexanderson and L. H. Lange in their obituary of Polya as “a mathematical masterpiece that assured their reputations.”
That book appeared in 1925, after Polya had obtained a Rockefeller Fellowship to work in England, where he collaborated with Hardy and Littlewood on what later became their book Inequalities (Cambridge University Press, 1936). He used a second Rockefeller Fellowship to visit Princeton University in 1933, and while in the United States was invited by H. F. Blichfeldt to visit Stanford University, which he greatly enjoyed, and which ultimately became his home. Polya held a professorship at Stanford from 1943 until his retirement in 1953, and it was there, in 1978, that he taught his last course, in combinatorics; he died on September 7, 1985, at the age of ninety-seven.
该书于 1925 年出版，此前波利亚获得洛克菲勒奖学金在英国工作，在那里他与哈代和利特尔伍德合作完成了后来的《不等式》一书（剑桥大学出版社，1936）。1933 年，他利用第二笔洛克菲勒奖学金访问了普林斯顿大学，在美国期间，他受 H·F.Blichfeldt 邀请访问了斯坦福大学，他非常喜欢那里，那里最终成为他的家。波利亚从 1943 年开始在斯坦福大学担任教授，直到 1953 年退休，1978 年，他在那里教授了他的最后一门课程，即组合学；他于 1985 年 9 月 7 日去世，享年 97 岁。
Some readers will want to know about Polya’s many contributions to mathematics. Most of them relate to analysis and are too technical to be understood by non-experts, but a few are worth mentioning.
有些读者会想知道波利亚对数学的许多贡献。其中大部分与分析有关，技术性太强，非专业人士无法理解，但有几项是值得一提的。
In probability theory, Polya is responsible for the now-standard term “Central Limit Theorem” and for proving that the Fourier transform of a probability measure is a characteristic function and that a random walk on the integer lattice closes with probability 1 if and only if the dimension is at most 2.
在概率论中，波利亚对现在的标准术语 “中心极限定理” 负责，并证明了概率度量的傅里叶变换是一个特征函数，以及当且仅当维数最多为 2 时，整数网格上的随机行走关闭的概率为 1。
In geometry, Polya independently re-enumerated the seventeen plane crystallographic groups (their first enumeration, by E. S. Fedorov, having been forgotten) and together with P. Niggli devised a notation for them.
在几何学方面，波利亚独立地重新列举了 17 个平面晶体学群（由 E·S·费多罗夫首次列举的这些群已被遗忘），并与 P·尼格利一起为它们设计了一个符号。
How to Solve It was written in German during Polya’s time in Zürich, which ended in 1940, when the European situation forced him to leave for the United States. Despite the book’s eventual success, four publishers rejected the English version before Princeton University Press brought it out in 1945. In their hands, How to Solve It rapidly became—and continues to be—one of the most successful mathematical books of all time.
如何解决》是波利亚在苏黎世期间用德语写的，苏黎世的生活于 1940 年结束，当时欧洲的形势迫使他去了美国。尽管这本书最终获得了成功，但在普林斯顿大学出版社于 1945 年将其推出之前，有四家出版商拒绝了其英文版本。在他们手中，《如何解题》迅速成为 —— 并继续成为 —— 有史以来最成功的数学书籍之一。
1The following biographical information is taken from that given by J. J. O’Connor and E. F. Robertson in the MacTutor History of Mathematics Archive (www-gap.dcs.st-and.ac.uk/~history/).
1以下传记资料取自 J·J. O'Connor 和 E·F. Robertson 在 MacTutor 数学史档案（www-gap.dcs.st-and.ac.uk/~history/）中提供的资料。
The following considerations are grouped around the preceding list of questions and suggestions entitled “How to Solve It.” Any question or suggestion quoted from it will be printed in italics, and the whole list will be referred to simply as “the list” or as “our list.”
下面的考虑是围绕着前面题为 “如何解决” 的问题和建议清单进行的。其中引用的任何问题或建议都将以斜体字印刷，而整个清单将被简单地称为 “清单” 或 “我们的清单”。
The following pages will discuss the purpose of the list, illustrate its practical use by examples, and explain the underlying notions and mental operations. By way of preliminary explanation, this much may be said: If, using them properly, you address these questions and suggestions to yourself, they may help you to solve your problem. If, using them properly, you address the same questions and suggestions to one of your students, you may help him to solve his problem.
下面几页将讨论清单的目的，通过实例说明其实际用途，并解释基本概念和心理操作。作为初步解释，可以说这么多。如果使用得当，你向自己提出这些问题和建议，它们可能有助于你解决问题。如果你正确地使用它们，向你的学生提出同样的问题和建议，你可能会帮助他解决他的问题。
The book is divided into four parts.
该书分为四个部分。
The title of the first part is “In the Classroom.” It contains twenty sections. Each section will be quoted by its number in heavy type as, for instance, “section 7.” Sections 1 to 5 discuss the “Purpose” of our list in general terms. Sections 6 to 17 explain what are the “Main Divisions, Main Questions” of the list, and discuss a first practical example. Sections 18, 19, 20 add “More Examples.”
第一部分的标题是 “在课堂上”。它包含 20 个部分。每一节都会用大号字体引用其编号，例如，“第 7 节”。第 1 至 5 节一般性地讨论了我们清单的 “目的”。第 6 至 17 节解释了清单的 “主要部门、主要问题”，并讨论了第一个实际例子。第 18、19、20 节增加了 “更多的例子”。
The title of the very short second part is “How to Solve It.” It is written in dialogue; a somewhat idealized teacher answers short questions of a somewhat idealized student.
非常短的第二部分的标题是 “如何解决”。它是以对话的形式写的；一个有点理想化的老师回答一个有点理想化的学生的简短问题。
The third and most extensive part is a “Short Dictionary of Heuristic”; we shall refer to it as the “Dictionary.” It contains sixty-seven articles arranged alphabetically. For example, the meaning of the term HEURISTIC (set in small capitals) is explained in an article with this title on page 112. When the title of such an article is referred to within the text it will be set in small capitals. Certain paragraphs of a few articles are more technical; they are enclosed in square brackets. Some articles are fairly closely connected with the first part to which they add further illustrations and more specific comments. Other articles go somewhat beyond the aim of the first part of which they explain the background. There is a key-article on MODERN HEURISTIC. It explains the connection of the main articles and the plan underlying the Dictionary; it contains also directions how to find information about particular items of the list. It must be emphasized that there is a common plan and a certain unity, because the articles of the Dictionary show the greatest outward variety. There are a few longer articles devoted to the systematic though condensed discussion of some general theme; others contain more specific comments, still others cross-references, or historical data, or quotations, or aphorisms, or even jokes.
第三部分也是最广泛的部分是 “启发式简明词典”；我们将把它称为 “词典”。它包含六十七条按字母顺序排列的条款。例如，术语HEURISTIC（用小写字母设置）的含义在第 112 页的一篇文章中以这个标题进行了解释。当文本中提到此类文章的标题时，它将以小写字母表示。一些文章的某些段落更具技术性；它们被置于方括号内。有些文章与第一部分有相当密切的联系，它们在第一部分中增加了进一步的插图和更具体的评论。其他文章在一定程度上超出了第一部分的目的，它们解释了其背景。有一篇关于《现代赫尔辛基》的关键文章。它解释了主要条款的联系和《辞海》的基本计划；它还包含了如何寻找清单中特定项目信息的指示。必须强调的是，有一个共同的计划和一定的统一性，因为《辞海》的文章显示出最大的外在多样性。有几篇较长的文章专门对一些一般的主题进行系统的、浓缩的讨论；其他的文章包含更具体的评论，还有一些是交叉引用，或历史数据，或引文，或箴言，甚至笑话。
The Dictionary should not be read too quickly; its text is often condensed, and now and then somewhat subtle. The reader may refer to the Dictionary for information about particular points. If these points come from his experience with his own problems or his own students, the reading has a much better chance to be profitable.
词典》不应阅读得太快；它的文字往往是浓缩的，而且时而有些微妙。读者可以参考《辞海》中关于特定要点的信息。如果这些要点来自于他对自己的问题或自己的学生的经验，那么阅读就更有可能获得收益。
The title of the fourth part is “Problems, Hints, Solutions.” It proposes a few problems to the more ambitious reader. Each problem is followed (in proper distance) by a “hint” that may reveal a way to the result which is explained in the “solution.”
第四部分的标题是 “问题、提示、解决方案”。它向更有野心的读者提出了几个问题。每个问题后面都有一个 “提示”（以适当的距离），可能揭示了通往 “解决方案” 中解释的结果的方法。
We have mentioned repeatedly the “student” and the “teacher” and we shall refer to them again and again. It may be good to observe that the “student” may be a high school student, or a college student, or anyone else who is studying mathematics. Also the “teacher” may be a high school teacher, or a college instructor, or anyone interested in the technique of teaching mathematics. The author looks at the situation sometimes from the point of view of the student and sometimes from that of the teacher (the latter case is preponderant in the first part). Yet most of the time (especially in the third part) the point of view is that of a person who is neither teacher nor student but anxious to solve the problem before him.
The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help or with insufficient help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.
学生应该尽可能多地获得独立工作的经验。但是，如果让他独自解决自己的问题，没有任何帮助或帮助不足，他可能根本就不会取得进展。如果老师帮助太多，学生就会一无所获。老师应该提供帮助，但不能太多，也不能太少，这样学生才会有合理的工作份额。
If the student is not able to do much, the teacher should leave him at least some illusion of independent work. In order to do so, the teacher should help the student discreetly, unobtrusively.
如果学生不能做很多事情，老师至少应该给他留下一些独立工作的假象。为了做到这一点，老师应该谨慎地、不引人注意地帮助学生。
The best is, however, to help the student naturally. The teacher should put himself in the student’s place, he should see the student’s case, he should try to understand what is going on in the student’s mind, and ask a question or indicate a step that could have occurred to the student himself.
然而，最好的办法是自然地帮助学生。老师应该把自己放在学生的位置上，他应该看到学生的情况，他应该试着理解学生的想法，并提出一个问题或指出一个学生自己可能想到的步骤。
2. Questions, recommendations, mental operations. Trying to help the student effectively but unobtrusively and naturally, the teacher is led to ask the same questions and to indicate the same steps again and again. Thus, in countless problems, we have to ask the question: What is the unknown? We may vary the words, and ask the same thing in many different ways: What is required? What do you want to find? What are you supposed to seek? The aim of these questions is to focus the student’s attention upon the unknown. Sometimes, we obtain the same effect more naturally with a suggestion: Look at the unknown! Question and suggestion aim at the same effect; they tend to provoke the same mental operation.
It seemed to the author that it might be worth while to collect and to group questions and suggestions which are typically helpful in discussing problems with students. The list we study contains questions and suggestions of this sort, carefully chosen and arranged; they are equally useful to the problem-solver who works by himself. If the reader is sufficiently acquainted with the list and can see, behind the suggestion, the action suggested, he may realize that the list enumerates, indirectly, mental operations typically useful for the solution of problems. These operations are listed in the order in which they are most likely to occur.
在作者看来，收集并归纳那些在与学生讨论问题时通常有帮助的问题和建议可能是值得的。我们研究的清单包含了精心选择和安排的这类问题和建议；它们对自己工作的问题解决者同样有用。如果读者对清单有足够的了解，并能看到建议背后所建议的行动，他可能会意识到，清单间接地列举了通常对解决问题有用的心理操作。这些操作是按照它们最可能发生的顺序排列的。
3. Generality is an important characteristic of the questions and suggestions contained in our list. Take the questions: What is the unknown? What are the data? What is the condition? These questions are generally applicable, we can ask them with good effect dealing with all sorts of problems. Their use is not restricted to any subject-matter. Our problem may be algebraic or geometric, mathematical or nonmathematical, theoretical or practical, a serious problem or a mere puzzle; it makes no difference, the questions make sense and might help us to solve the problem.
There is a restriction, in fact, but it has nothing to do with the subject-matter. Certain questions and suggestions of the list are applicable to “problems to find” only, not to “problems to prove.” If we have a problem of the latter kind we must use different questions; see PROBLEMS TO FIND, PROBLEMS TO PROVE.
4. Common sense. The questions and suggestions of our list are general, but, except for their generality, they are natural, simple, obvious, and proceed from plain common sense. Take the suggestion: Look at the unknown! And try to think of a familiar problem having the same or a similar unknown. This suggestion advises you to do what you would do anyhow, without any advice, if you were seriously concerned with your problem. Are you hungry? You wish to obtain food and you think of familiar ways of obtaining food. Have you a problem of geometric construction? You wish to construct a triangle and you think of familiar ways of constructing a triangle. Have you a problem of any kind? You wish to find a certain unknown, and you think of familiar ways of finding such an unknown, or some similar unknown. If you do so you follow exactly the suggestion we quoted from our list. And you are on the right track, too; the suggestion is a good one, it suggests to you a procedure which is very frequently successful.
4.4. 常识。我们清单上的问题和建议都很笼统，但除了笼统之外，它们都是自然的、简单的、明显的，并且来自于普通的常识。就拿这个建议来说吧。看看未知的东西!并试着去想一个熟悉的问题，有相同或类似的未知数。这个建议建议你做你无论如何都会做的事情，不需要任何建议，如果你认真关注你的问题。你饿了吗？你希望获得食物，你想到了熟悉的获得食物的方法。你有一个几何结构的问题吗？你希望构建一个三角形，你想到了熟悉的构建三角形的方法。你有任何类型的问题吗？你希望找到某个未知数，而你想到了找到这样一个未知数或一些类似的未知数的熟悉方法。如果你这样做了，你就完全遵循了我们在清单中引用的建议。而且你也在正确的轨道上；这个建议是个好建议，它向你建议了一个经常成功的程序。
All the questions and suggestions of our list are natural, simple, obvious, just plain common sense; but they state plain common sense in general terms. They suggest a certain conduct which comes naturally to any person who is seriously concerned with his problem and has some common sense. But the person who behaves the right way usually does not care to express his behavior in clear words and, possibly, he cannot express it so; our list tries to express it so.
我们清单上的所有问题和建议都是自然的、简单的、显而易见的，只是普通的常识；但它们是以一般的术语陈述普通的常识。它们建议了某种行为，对于任何认真关注自己问题并有一定常识的人来说，这种行为是自然而然的。但是，行为正确的人通常不屑于用明确的语言来表达他的行为，而且，可能他不能这样表达；我们的清单试图这样表达。
5. Teacher and student. Imitation and practice. There are two aims which the teacher may have in view when addressing to his students a question or a suggestion of the list: First, to help the student to solve the problem at hand. Second, to develop the student’s ability so that he may solve future problems by himself.
Experience shows that the questions and suggestions of our list, appropriately used, very frequently help the student. They have two common characteristics, common sense and generality. As they proceed from plain common sense they very often come naturally; they could have occurred to the student himself. As they are general, they help unobtrusively; they just indicate a general direction and leave plenty for the student to do.
经验表明，我们清单上的问题和建议，如果使用得当，往往能帮助学生。它们有两个共同的特点：常识性和一般性。由于它们来自于普通的常识，所以往往是自然而然的；它们可能是学生自己想到的。由于它们是一般性的，所以它们的帮助是不明显的；它们只是指出了一个大方向，并为学生留下了很多事情要做。
But the two aims we mentioned before are closely connected; if the student succeeds in solving the problem at hand, he adds a little to his ability to solve problems. Then, we should not forget that our questions are general, applicable in many cases. If the same question is repeatedly helpful, the student will scarcely fail to notice it and he will be induced to ask the question by himself in a similar situation. Asking the question repeatedly, he may succeed once in eliciting the right idea. By such a success, he discovers the right way of using the question, and then he has really assimilated it.
但我们之前提到的两个目的是紧密相连的；如果学生成功地解决了手头的问题，他就为自己解决问题的能力增加了一点。然后，我们不应忘记，我们的问题是一般性的，适用于许多情况。如果同样的问题反复出现，学生几乎不会注意到它，他就会被诱导在类似的情况下自己问这个问题。反复问这个问题，他可能一次就能成功地引出正确的想法。通过这样的成功，他发现了使用该问题的正确方法，然后他就真正吸收了该问题。
The student may absorb a few questions of our list so well that he is finally able to put to himself the right question in the right moment and to perform the corresponding mental operation naturally and vigorously. Such a student has certainly derived the greatest possible profit from our list. What can the teacher do in order to obtain this best possible result?
学生可能会很好地吸收我们清单上的几个问题，以至于他最终能够在正确的时刻向自己提出正确的问题，并自然而有力地进行相应的心理操作。这样的学生肯定已经从我们的清单中获得了最大可能的收益。为了获得这种最好的结果，教师可以做些什么？
Solving problems is a practical skill like, let us say, swimming. We acquire any practical skill by imitation and practice. Trying to swim, you imitate what other people do with their hands and feet to keep their heads above water, and, finally, you learn to swim by practicing swimming. Trying to solve problems, you have to observe and to imitate what other people do when solving problems and, finally, you learn to do problems by doing them.
The teacher who wishes to develop his students’ ability to do problems must instill some interest for problems into their minds and give them plenty of opportunity for imitation and practice. If the teacher wishes to develop in his students the mental operations which correspond to the questions and suggestions of our list, he puts these questions and suggestions to the students as often as he can do so naturally. Moreover, when the teacher solves a problem before the class, he should dramatize his ideas a little and he should put to himself the same questions which he uses when helping the students. Thanks to such guidance, the student will eventually discover the right use of these questions and suggestions, and doing so he will acquire something that is more important than the knowledge of any particular mathematical fact.
希望培养学生做题能力的老师，必须在他们的头脑中灌输一些对问题的兴趣，并给他们足够的机会进行模仿和练习。如果教师希望培养学生与我们清单中的问题和建议相对应的心理操作，那么他就要经常向学生提出这些问题和建议，只要他能自然地这样做。此外，当教师在课堂上解决一个问题时，他应该将自己的想法稍加渲染，并向自己提出他在帮助学生时使用的同样问题。由于这样的指导，学生最终会发现这些问题和建议的正确使用，这样做他将获得比任何特定数学事实的知识更重要的东西。
6. Four phases. Trying to find the solution, we may repeatedly change our point of view, our way of looking at the problem. We have to shift our position again and again. Our conception of the problem is likely to be rather incomplete when we start the work; our outlook is different when we have made some progress; it is again different when we have almost obtained the solution.
In order to group conveniently the questions and suggestions of our list, we shall distinguish four phases of the work. First, we have to understand the problem; we have to see clearly what is required. Second, we have to see how the various items are connected, how the unknown is linked to the data, in order to obtain the idea of the solution, to make a plan. Third, we carry out our plan. Fourth, we look back at the completed solution, we review and discuss it.
Each of these phases has its importance. It may happen that a student hits upon an exceptionally bright idea and jumping all preparations blurts out with the solution. Such lucky ideas, of course, are most desirable, but something very undesirable and unfortunate may result if the student leaves out any of the four phases without having a good idea. The worst may happen if the student embarks upon computations or constructions without having understood the problem. It is generally useless to carry out details without having seen the main connection, or having made a sort of plan. Many mistakes can be avoided if, carrying out his plan, the student checks each step. Some of the best effects may be lost if the student fails to reexamine and to reconsider the completed solution.
这些阶段中的每一个都有其重要性。可能发生的情况是，一个学生想到了一个非常聪明的想法，并在所有的准备工作中脱口而出，说出了解决方案。这种幸运的想法当然是最理想的，但如果学生在没有好的想法的情况下离开了这四个阶段中的任何一个，可能会导致一些非常不理想和不幸的结果。如果学生在没有理解问题的情况下就开始计算或建造，可能会发生最糟糕的情况。一般来说，在没有看到主要联系或没有做出某种计划的情况下，进行细节处理是没有用的。如果在执行计划时，学生检查每一个步骤，就可以避免许多错误。如果学生不能重新检查和重新考虑已完成的解决方案，一些最好的效果可能就会丧失。
7. Understanding the problem. It is foolish to answer a question that you do not understand. It is sad to work for an end that you do not desire. Such foolish and sad things often happen, in and out of school, but the teacher should try to prevent them from happening in his class. The student should understand the problem. But he should not only understand it, he should also desire its solution. If the student is lacking in understanding or in interest, it is not always his fault; the problem should be well chosen, not too difficult and not too easy, natural and interesting, and some time should be allowed for natural and interesting presentation.
First of all, the verbal statement of the problem must be understood. The teacher can check this, up to a certain extent; he asks the student to repeat the statement, and the student should be able to state the problem fluently. The student should also be able to point out the principal parts of the problem, the unknown, the data, the condition. Hence, the teacher can seldom afford to miss the questions: What is the unknown? What are the data? What is the condition?
The student should consider the principal parts of the problem attentively, repeatedly, and from various sides. If there is a figure connected with the problem he should draw a figure and point out on it the unknown and the data. If it is necessary to give names to these objects he should introduce suitable notation; devoting some attention to the appropriate choice of signs, he is obliged to consider the objects for which the signs have to be chosen. There is another question which may be useful in this preparatory stage provided that we do not expect a definitive answer but just a provisional answer, a guess: Is it possible to satisfy the condition?
学生应该认真地、反复地、从不同方面考虑问题的主要部分。如果有一个与问题相关的图形，他应该画一个图形并在上面指出未知数和数据。如果有必要给这些对象命名，他应该引入合适的符号；对符号的适当选择给予一定的关注，他有义务考虑必须为其选择符号的对象。在这个准备阶段，还有一个问题可能是有用的，只要我们不期待一个明确的答案，而只是一个临时的答案，一个猜测：有可能满足条件吗？
In order to discuss this problem profitably, the students must be familiar with the theorem of Pythagoras, and with some of its applications in plane geometry, but they may have very little systematic knowledge in solid geometry. The teacher may rely here upon the student’s unsophisticated familiarity with spatial relations.
为了有效地讨论这个问题，学生必须熟悉毕达哥拉斯定理，以及它在平面几何中的一些应用，但他们可能对实体几何的系统知识了解甚少。在这里，教师可以依靠学生对空间关系的不成熟的熟悉程度。
The teacher can make the problem interesting by making it concrete. The classroom is a rectangular parallelepiped whose dimensions could be measured, and can be estimated; the students have to find, to “measure indirectly,” the diagonal of the classroom. The teacher points out the length, the width, and the height of the classroom, indicates the diagonal with a gesture, and enlivens his figure, drawn on the blackboard, by referring repeatedly to the classroom.
The dialogue between the teacher and the students may start as follows:
教师和学生之间的对话可按以下方式开始。
“What is the unknown?”
“未知的是什么？”
“The length of the diagonal of a parallelepiped.”
“平行四边形的对角线的长度”。
“What are the data?”
“数据是什么？”
“The length, the width, and the height of the parallelepiped.”
“平行四边形的长度、宽度和高度。”
“Introduce suitable notation. Which letter should denote the unknown?”
“介绍合适的符号。哪个字母应该表示未知数？”
“x.”
“x.”
“Which letters would you choose for the length, the width, and the height?”
“你会选择哪些字母作为长度、宽度和高度？”
“a, b, c.”
“A、B、C。”
“What is the condition, linking a, b, c, and x?”
“什么是条件，把a、b、c和x联系起来？”
“x is the diagonal of the parallelepiped of which a, b, and c are the length, the width, and the height.”
“x是平行四边形的对角线，其中a、b和c是长度、宽度和高度。”
“Is it a reasonable problem? I mean, is the condition sufficient to determine the unknown?”
“这是一个合理的问题吗？我的意思是，这个条件是否足以确定未知数？”
“Yes, it is. If we know a, b, c, we know the parallelepiped. If the parallelepiped is determined, the diagonal is determined.”
“是的，它是。如果我们知道a、b、c，我们就知道平行四边形。如果平行四边形被确定，那么对角线就被确定了。”
9. Devising a plan. We have a plan when we know, or know at least in outline, which calculations, computations, or constructions we have to perform in order to obtain the unknown. The way from understanding the problem to conceiving a plan may be long and tortuous. In fact, the main achievement in the solution of a problem is to conceive the idea of a plan. This idea may emerge gradually. Or, after apparently unsuccessful trials and a period of hesitation, it may occur suddenly, in a flash, as a “bright idea.” The best that the teacher can do for the student is to procure for him, by unobtrusive help, a bright idea. The questions and suggestions we are going to discuss tend to provoke such an idea.
In order to be able to see the student’s position, the teacher should think of his own experience, of his difficulties and successes in solving problems.
为了能够看到学生的立场，教师应该想到自己的经验，想到自己解决问题的困难和成功。
We know, of course, that it is hard to have a good idea if we have little knowledge of the subject, and impossible to have it if we have no knowledge. Good ideas are based on past experience and formerly acquired knowledge. Mere remembering is not enough for a good idea, but we cannot have any good idea without recollecting some pertinent facts; materials alone are not enough for constructing a house but we cannot construct a house without collecting the necessary materials. The materials necessary for solving a mathematical problem are certain relevant items of our formerly acquired mathematical knowledge, as formerly solved problems, or formerly proved theorems. Thus, it is often appropriate to start the work with the question: Do you know a related problem?
当然，我们知道，如果我们对这个主题的知识很少，就很难有好的想法，如果我们没有知识，就不可能有。好的想法是基于过去的经验和以前获得的知识。仅仅记住是不够的，但如果不回忆一些相关的事实，我们就不可能有任何好的想法；仅有材料是不够的，但如果不收集必要的材料，我们就无法建造房屋。解决数学问题的必要材料是我们以前获得的数学知识中的某些相关项目，如以前解决的问题，或以前证明的定理。因此，以问题开始工作往往是合适的。你知道一个相关的问题吗？
The difficulty is that there are usually too many problems which are somewhat related to our present problem, that is, have some point in common with it. How can we choose the one, or the few, which are really useful? There is a suggestion that puts our finger on an essential common point: Look at the unknown! And try to think of a familiar problem having the same or a similar unknown.
困难在于，通常有太多的问题与我们目前的问题有一定的关联，也就是说，与它有一些共同点。我们怎样才能选择一个或几个真正有用的问题呢？有一个建议可以把我们的手指放在一个基本的共同点上。看看未知的东西!试着去想一个熟悉的问题，它具有相同或类似的未知性。
If we succeed in recalling a formerly solved problem which is closely related to our present problem, we are lucky. We should try to deserve such luck; we may deserve it by exploiting it. Here is a problem related to yours and solved before. Could you use it?
如果我们成功地回忆起一个以前解决的问题，而这个问题与我们现在的问题密切相关，我们就是幸运的。我们应该努力配得上这种运气；我们可以通过利用它来配得上这种运气。这里有一个与你有关的、以前解决过的问题。你能利用它吗？
The foregoing questions, well understood and seriously considered, very often help to start the right train of ideas; but they cannot help always, they cannot work magic. If they do not work, we must look around for some other appropriate point of contact, and explore the various aspects of our problem; we have to vary, to transform, to modify the problem. Could you restate the problem? Some of the questions of our list hint specific means to vary the problem, as generalization, specialization, use of analogy, dropping a part of the condition, and so on; the details are important but we cannot go into them now. Variation of the problem may lead to some appropriate auxiliary problem: If you cannot solve the proposed problem try to solve first some related problem.
Trying to apply various known problems or theorems, considering various modifications, experimenting with various auxiliary problems, we may stray so far from our original problem that we are in danger of losing it altogether. Yet there is a good question that may bring us back to it: Did you use all the data? Did you use the whole condition?
试图应用各种已知的问题或定理，考虑各种修改，试验各种辅助问题，我们可能会偏离我们最初的问题，以至于我们有可能完全失去它。然而，有一个很好的问题可能会让我们回到这个问题上。你使用了所有的数据吗？你使用了整个条件吗？
10. Example. We return to the example considered in section 8. As we left it, the students just succeeded in understanding the problem and showed some mild interest in it. They could now have some ideas of their own, some initiative. If the teacher, having watched sharply, cannot detect any sign of such initiative he has to resume carefully his dialogue with the students. He must be prepared to repeat with some modification the questions which the students do not answer. He must be prepared to meet often with the disconcerting silence of the students (which will be indicated by dots . . . . .).
“Do you know a related problem?”
“你知道一个相关的问题吗？”
. . . . .
…… . . .
“Look at the unknown! Do you know a problem having the same unknown?”
“看看这个未知数!你知道有一个问题有同样的未知数吗？”
. . . . .
…… . . .
“Well, what is the unknown?”
“那么，未知的是什么呢？”
“Do you know any problem with the same unknown?”
“你知道有什么问题是同样未知的吗？”
“No. We have not had any problem yet about the diagonal of a parallelepiped.”
“不，我们还没有遇到关于平行四边形的对角线的问题。”
“Do you know any problem with a similar unknown?”
“你知道有什么类似的未知问题吗？”
. . . . .
…… . . .
“You see, the diagonal is a segment, the segment of a straight line. Did you never solve a problem whose unknown was the length of a line?”
“你看，对角线是一条线段，是一条直线的线段。你从来没有解决过一个未知数是直线长度的问题吗？”
“Of course, we have solved such problems. For instance, to find a side of a right triangle.”
“当然，我们已经解决了这样的问题。例如，找到一个直角三角形的边。”
“Good! Here is a problem related to yours and solved before. Could you use it?”
“很好!这里有一个与你有关的问题，以前也解决过。你可以使用它吗？”
. . . . .
…… . . .
“You were lucky enough to remember a problem which is related to your present one and which you solved before. Would you like to use it? Could you introduce some auxiliary element in order to make its use possible?”
“你很幸运，记得一个与你现在的问题有关的问题，而且你以前也解决过。你想使用它吗？你能不能引入一些辅助元素，以便使其使用成为可能？”
FIG. 1
图 1
. . . . .
…… . . .
“Look here, the problem you remembered is about a triangle. Have you any triangle in your figure?”
“看这里，你记得的问题是关于一个三角形的。你的图中有任何三角形吗？”
Let us hope that the last hint was explicit enough to provoke the idea of the solution which is to introduce a right triangle, (emphasized in Fig. 1) of which the required diagonal is the hypotenuse. Yet the teacher should be prepared for the case that even this fairly explicit hint is insufficient to shake the torpor of the students; and so he should be prepared to use a whole gamut of more and more explicit hints.
让我们希望最后一个提示足够明确，以激发学生对解决方案的想法，即引入一个直角三角形，（在图 1中强调），其中所需的对角线是斜边。然而，教师应该做好准备，即使是这种相当明确的提示也不足以撼动学生的情绪；因此，他应该准备好使用更多、更明确的提示的整个范围。
“Would you like to have a triangle in the figure?”
“你想在图中有一个三角形吗？”
“What sort of triangle would you like to have in the figure?”
“你希望在图中有什么样的三角形？”
“You cannot find yet the diagonal; but you said that you could find the side of a triangle. Now, what will you do?”
“你还不能找到对角线；但你说你能找到三角形的边。现在，你打算怎么做？”
“Could you find the diagonal, if it were a side of a triangle?”
“你能找到对角线吗，如果它是三角形的一条边？”
When, eventually, with more or less help, the students succeed in introducing the decisive auxiliary element, the right triangle emphasized in Fig. 1, the teacher should convince himself that the students see sufficiently far ahead before encouraging them to go into actual calculations.
当最终，在或多或少的帮助下，学生成功地引入了决定性的辅助元素，即图 1中强调的直角三角形，教师应该说服自己，在鼓励他们进入实际计算之前，学生已经看到了足够的前景。
“I think that it was a good idea to draw that triangle. You have now a triangle; but have you the unknown?”
“我认为，画这个三角形是个好主意。你现在有了一个三角形；但你有了未知的东西吗？”
“The unknown is the hypotenuse of the triangle; we can calculate it by the theorem of Pythagoras.”
“未知数是三角形的斜边；我们可以通过毕达哥拉斯定理来计算它。”
“You can, if both legs are known; but are they?”
“你可以，如果两条腿都知道；但他们是吗？”
“One leg is given, it is c. And the other, I think, is not difficult to find. Yes, the other leg is the hypotenuse of another right triangle.”
“一条腿已经给了，是c，而另一条，我想，不难找到。是的，另一条腿是另一个直角三角形的斜边。”
“Very good! Now I see that you have a plan.”
“很好!现在我看到，你有一个计划。”
11. Carrying out the plan. To devise a plan, to conceive the idea of the solution is not easy. It takes so much to succeed; formerly acquired knowledge, good mental habits, concentration upon the purpose, and one more thing: good luck. To carry out the plan is much easier; what we need is mainly patience.
If the student has really conceived a plan, the teacher has now a relatively peaceful time. The main danger is that the student forgets his plan. This may easily happen if the student received his plan from outside, and accepted it on the authority of the teacher; but if he worked for it himself, even with some help, and conceived the final idea with satisfaction, he will not lose this idea easily. Yet the teacher must insist that the student should check each step.
如果学生真的构思了一个计划，老师现在就有了一个相对平静的时间。主要的危险是，学生忘记了他的计划。如果学生从外面得到他的计划，并在老师的授权下接受它，这种情况很容易发生；但如果他自己努力，甚至有一些帮助，并满意地构想出最后的想法，他不会轻易失去这个想法。然而，老师必须坚持让学生检查每一个步骤。
We may convince ourselves of the correctness of a step in our reasoning either “intuitively” or “formally.” We may concentrate upon the point in question till we see it so clearly and distinctly that we have no doubt that the step is correct; or we may derive the point in question according to formal rules. (The difference between “insight” and “formal proof” is clear enough in many important cases; we may leave further discussion to philosophers.)
我们可以通过 “直觉” 或 “形式” 来说服自己相信我们推理中某一步骤的正确性。我们可以把注意力集中在有关的点上，直到我们清楚明白地看到它，以至于我们毫不怀疑这个步骤是正确的；或者我们可以根据正式的规则推导出有关的点。（在许多重要的情况下，“洞察力” 和 “正式证明” 之间的区别是很清楚的；我们可以把进一步的讨论留给哲学家们）。
The main point is that the student should be honestly convinced of the correctness of each step. In certain cases, the teacher may emphasize the difference between “seeing” and “proving”: Can you see clearly that the step is correct? But can you also prove that the step is correct?
主要的一点是，学生应该诚实地相信每个步骤的正确性。在某些情况下，教师可能会强调 “看到” 和 “证明” 之间的区别。你能清楚地看到这个步骤是正确的吗？但你也能证明这个步骤是正确的吗？
12. Example. Let us resume our work at the point where we left it at the end of section 10. The student, at last, has got the idea of the solution. He sees the right triangle of which the unknown x is the hypotenuse and the given height c is one of the legs; the other leg is the diagonal of a face. The student must, possibly, be urged to introduce suitable notation. He should choose y to denote that other leg, the diagonal of the face whose sides are a and b. Thus, he may see more clearly the idea of the solution which is to introduce an auxiliary problem whose unknown is y. Finally, working at one right triangle after the other, he may obtain (see Fig. 1)
12. 例子。让我们从第 10 节结束时的位置继续我们的工作。学生终于得到了解决问题的思路。他看到了一个直角三角形，其中未知的x是斜边，给定的高度c是其中一条腿；另一条腿是一个面的对角线。可能的话，必须敦促学生引入合适的符号。他应该选择y来表示另一条腿，即面的对角线，其边。这样，他可能会更清楚地看到解决方案的想法，即引入一个辅助问题，其未知数是y。最后，在一个又一个的直角三角形中工作，他可以得到（见图 1）。
and hence, eliminating the auxiliary unknown y,
因此，消除了辅助性的未知数y。
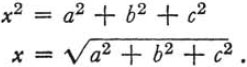
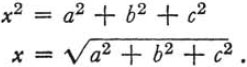
The teacher has no reason to interrupt the student if he carries out these details correctly except, possibly, to warn him that he should check each step. Thus, the teacher may ask:
如果学生正确地执行了这些细节，教师没有理由打断他，除了可能的话，警告他应该检查每一个步骤。因此，老师可以问
“Can you see clearly that the triangle with sides x, y, c is a right triangle?”
“你能清楚地看到边长为x、y、c的三角形是一个直角三角形吗？”
To this question the student may answer honestly “Yes” but he could be much embarrassed if the teacher, not satisfied with the intuitive conviction of the student, should go on asking:
对于这个问题，学生可以诚实地回答 “是”，但如果老师不满意学生的直觉信念，继续问下去，他可能会很尴尬。
“But can you prove that this triangle is a right triangle?”
“但你能证明这个三角形是一个直角三角形吗？”
Thus, the teacher should rather suppress this question unless the class has had a good initiation in solid geometry. Even in the latter case, there is some danger that the answer to an incidental question may become the main difficulty for the majority of the students.
因此，教师应该抑制这个问题，除非这个班级在实体几何方面有一个良好的开端。即使在后一种情况下，也有一些危险，即对一个偶然问题的回答可能成为大多数学生的主要困难。
13. Looking back. Even fairly good students, when they have obtained the solution of the problem and written down neatly the argument, shut their books and look for something else. Doing so, they miss an important and instructive phase of the work. By looking back at the completed solution, by reconsidering and reexamining the result and the path that led to it, they could consolidate their knowledge and develop their ability to solve problems. A good teacher should understand and impress on his students the view that no problem whatever is completely exhausted. There remains always something to do; with sufficient study and penetration, we could improve any solution, and, in any case, we can always improve our understanding of the solution.
The student has now carried through his plan. He has written down the solution, checking each step. Thus, he should have good reasons to believe that his solution is correct. Nevertheless, errors are always possible, especially if the argument is long and involved. Hence, verifications are desirable. Especially, if there is some rapid and intuitive procedure to test either the result or the argument, it should not be overlooked. Can you check the result? Can you check the argument?
这个学生现在已经完成了他的计划。他已经写下了解决方案，检查了每一步。因此，他应该有充分的理由相信他的解决方案是正确的。然而，错误总是可能发生的，特别是当论证是漫长的和涉及的。因此，验证是可取的。特别是，如果有一些快速而直观的程序来检验结果或论证，就不应该被忽视。你能检查结果吗？你能检验论证吗？
In order to convince ourselves of the presence or of the quality of an object, we like to see and to touch it. And as we prefer perception through two different senses, so we prefer conviction by two different proofs: Can you derive the result differently? We prefer, of course, a short and intuitive argument to a long and heavy one: Can you see it at a glance?
为了使我们自己相信一个物体的存在或质量，我们喜欢看和触摸它。正如我们喜欢通过两种不同的感官来感知，我们也喜欢通过两种不同的证明来说服自己。你能以不同的方式推导出结果吗？当然，我们更喜欢简短而直观的论证，而不是冗长而沉重的论证。你能一目了然吗？
One of the first and foremost duties of the teacher is not to give his students the impression that mathematical problems have little connection with each other, and no connection at all with anything else. We have a natural opportunity to investigate the connections of a problem when looking back at its solution. The students will find looking back at the solution really interesting if they have made an honest effort, and have the consciousness of having done well. Then they are eager to see what else they could accomplish with that effort, and how they could do equally well another time. The teacher should encourage the students to imagine cases in which they could utilize again the procedure used, or apply the result obtained. Can you use the result, or the method, for some other problem?
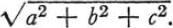
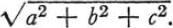
Can you check the result? The teacher cannot expect a good answer to this question from inexperienced students. The students, however, should acquire fairly early the experience that problems “in letters” have a great advantage over purely numerical problems; if the problem is given “in letters” its result is accessible to several tests to which a problem “in numbers” is not susceptible at all. Our example, although fairly simple, is sufficient to show this. The teacher can ask several questions about the result which the students may readily answer with “Yes”; but an answer “No” would show a serious flaw in the result.
你能检查出结果吗？对于这个问题，老师不能指望没有经验的学生能给出好的答案。然而，学生应该很早就获得这样的经验：“字母” 问题比纯粹的数字问题有很大的优势；如果问题是以 “字母” 形式给出的，其结果可以接受一些测试，而 “数字” 问题则根本不可能接受。我们的例子，虽然相当简单，但足以说明这一点。教师可以就结果提出几个问题，学生可以很容易地回答 “是”；但如果回答 “不是”，则表明结果存在严重缺陷。
“Did you use all the data? Do all the data a, b, c appear in your formula for the diagonal?”
“你使用了所有的数据吗？所有的数据a、b、c都出现在你的对角线公式中吗？”
“Length, width, and height play the same role in our question; our problem is symmetric with respect to a, b, c. Is the expression you obtained for the diagonal symmetric in a, b, c? Does it remain unchanged when a, b, c are interchanged?”
“长度、宽度和高度在我们的问题中起着同样的作用；我们的问题是关于a、b、c的对称问题。你得到的对角线的表达式在a、b、c中是对称的吗？当a、b、c互换时，它是否保持不变？”
“Our problem is a problem of solid geometry: to find the diagonal of a parallelepiped with given dimensions a, b, c. Our problem is analogous to a problem of plane geometry: to find the diagonal of a rectangle with given dimensions a, b. Is the result of our ‘solid’ problem analogous to the result of the ‘plane’ problem?”
“我们的问题是一个实体几何问题：寻找一个尺寸为a、b、c的平行四边形的对角线。我们的问题类似于一个平面几何问题：寻找一个尺寸为a、b的矩形的对角线。
“If the height c increases, the diagonal increases. Does your formula show this?”
“如果高度c增加，对角线就会增加。你的公式是否显示了这一点？”
“If all three measures a, b, c of the parallelepiped increase in the same proportion, the diagonal also increases in the same proportion. If, in your formula, you substitute 12a, 12b, 12c for a, b, c respectively, the expression of the diagonal, owing to this substitution, should also be multiplied by 12. Is that so?”
“如果平行四边形的所有三个量度a、b、c以相同的比例增加，对角线也以相同的比例增加。如果在你的公式中，你用12a、12b、12c分别代替a、b、c，由于这种替换，对角线的表达也应该乘以 12。是这样吗？”
“If a, b, c are measured in feet, your formula gives the diagonal measured in feet too; but if you change all measures into inches, the formula should remain correct. Is that so?”
“如果a、b、c是以英尺为单位，你的公式也会给出以英尺为单位的对角线；但如果你把所有的测量值改为英寸，公式应该还是正确的。是这样吗？”
(The two last questions are essentially equivalent; see TEST BY DIMENSION.)
（最后两个问题基本上是等价的，见 “按尺寸测试”）。
These questions have several good effects. First, an intelligent student cannot help being impressed by the fact that the formula passes so many tests. He was convinced before that the formula is correct because he derived it carefully. But now he is more convinced, and his gain in confidence comes from a different source; it is due to a sort of “experimental evidence.” Then, thanks to the foregoing questions, the details of the formula acquire new significance, and are linked up with various facts. The formula has therefore a better chance of being remembered, the knowledge of the student is consolidated. Finally, these questions can be easily transferred to similar problems. After some experience with similar problems, an intelligent student may perceive the underlying general ideas: use of all relevant data, variation of the data, symmetry, analogy. If he gets into the habit of directing his attention to such points, his ability to solve problems may definitely profit.
这些问题有几个好的效果。首先，一个聪明的学生不能不对公式通过这么多测试这一事实印象深刻。他以前确信这个公式是正确的，因为他仔细地推导了它。但现在他更相信了，而且他的信心增加来自不同的来源；这是由于某种 “实验证据”。然后，由于前面的问题，公式的细节获得了新的意义，并与各种事实联系起来。因此，该公式有更好的机会被记住，学生的知识得到巩固。最后，这些问题可以很容易地转移到类似的问题上。经过对类似问题的一些经验，聪明的学生可能会察觉到潜在的一般想法：使用所有相关的数据，数据的变化，对称性，类比。如果他养成了把注意力放在这些点上的习惯，他解决问题的能力肯定会提高。
Can you check the argument? To recheck the argument step by step may be necessary in difficult and important cases. Usually, it is enough to pick out “touchy” points for rechecking. In our case, it may be advisable to discuss retrospectively the question which was less advisable to discuss as the solution was not yet attained: Can you prove that the triangle with sides x, y, c is a right triangle? (See the end of section 12.)
Can you use the result or the method for some other problem? With a little encouragement, and after one or two examples, the students easily find applications which consist essentially in giving some concrete interpretation to the abstract mathematical elements of the problem. The teacher himself used such a concrete interpretation as he took the room in which the discussion takes place for the parallelepiped of the problem. A dull student may propose, as application, to calculate the diagonal of the cafeteria instead of the diagonal of the classroom. If the students do not volunteer more imaginative remarks, the teacher himself may put a slightly different problem, for instance: “Being given the length, the width, and the height of a rectangular parallelepiped, find the distance of the center from one of the corners.”
你能将这个结果或方法用于其他问题吗？只要稍加鼓励，在一两个例子之后，学生们很容易找到应用，这主要是对问题的抽象数学元素做出一些具体的解释。老师自己就使用了这样的具体解释，因为他在讨论问题的平行四边形的房间里进行了讨论。一个呆板的学生可能会提议，作为应用，计算食堂的对角线而不是教室的对角线。如果学生没有自愿提出更有想象力的意见，教师可以自己提出一个稍微不同的问题，例如。“给定一个长方形平行四边形的长、宽、高，求中心与其中一个角的距离”。
The students may use the result of the problem they just solved, observing that the distance required is one half of the diagonal they just calculated. Or they may use the method, introducing suitable right triangles (the latter alternative is less obvious and somewhat more clumsy in the present case).
学生们可以使用他们刚刚解决的问题的结果，观察所需的距离是他们刚刚计算的对角线的一半。或者他们可以使用这个方法，引入合适的直角三角形（在目前的情况下，后一种选择不太明显，而且有些笨拙）。
After this application, the teacher may discuss the configuration of the four diagonals of the parallelepiped, and the six pyramids of which the six faces are the bases, the center the common vertex, and the semidiagonals the lateral edges. When the geometric imagination of the students is sufficiently enlivened, the teacher should come back to his question: Can you use the result, or the method, for some other problem? Now there is a better chance that the students may find some more interesting concrete interpretation, for instance, the following:
“In the center of the flat rectangular top of a building which is 21 yards long and 16 yards wide, a flagpole is to be erected, 8 yards high. To support the pole, we need four equal cables. The cables should start from the same point, 2 yards under the top of the pole, and end at the four corners of the top of the building. How long is each cable?”
“在一栋长 21 码、宽 16 码的平坦的长方形顶部中央，要竖起一根 8 码高的旗杆。为了支撑这根旗杆，我们需要四根相等的缆绳。这些缆绳应该从同一地点开始，在旗杆顶部下方 2 码处，并在建筑物顶部的四个角处结束。每条电缆有多长？”
The students may use the method of the problem they solved in detail introducing a right triangle in a vertical plane, and another one in a horizontal plane. Or they may use the result, imagining a rectangular parallelepiped of which the diagonal, x, is one of the four cables and the edges are
学生们可以使用他们解决的问题的方法，详细介绍垂直平面内的一个直角三角形，以及水平平面内的另一个直角三角形。或者他们可以使用这个结果，想象一个长方形的平行四边形，其对角线x是四条线中的一条，边缘是
By straightforward application of the formula, x = 14.5.
通过对公式的直接应用，x=14.5。
For more examples, see CAN YOU USE THE RESULT?
更多的例子，请参阅《你能使用这个结果吗？
15. Various approaches. Let us still retain, for a while, the problem we considered in the foregoing sections 8, 10, 12, 14. The main work, the discovery of the plan, was described in section 10. Let us observe that the teacher could have proceeded differently. Starting from the same point as in section 10, he could have followed a somewhat different line, asking the following questions:
“Do you know any related problem?”
“你知道任何相关的问题吗？”
“Do you know an analogous problem?”
“你知道一个类似的问题吗？”
“You see, the proposed problem is a problem of solid geometry. Could you think of a simpler analogous problem of plane geometry?”
“你看，提出的问题是一个实体几何的问题。你能想出一个更简单的平面几何的类似问题吗？”
“Parallelogram.”
“平行四边形”。
The students, even if they are very slow and indifferent, and were not able to guess anything before, are obliged finally to contribute at least a minute part of the idea. Besides, if the students are so slow, the teacher should not take up the present problem about the parallelepiped without having discussed before, in order to prepare the students, the analogous problem about the parallelogram. Then, he can go on now as follows:
学生们，即使他们非常迟钝和无动于衷，而且之前不能猜到任何东西，最后也有义务至少贡献出想法的一小部分。此外，如果学生的速度很慢，教师就不应该在没有讨论过平行四边形的类似问题之前就开始讨论这个问题，以便让学生有所准备。那么，他现在可以继续如下。
“Here is a problem related to yours and solved before. Can you use it?”
“这里有一个与你有关的问题，以前也解决过。你能使用它吗？”
“Should you introduce some auxiliary element in order to make its use possible?”
“你是否应该引入一些辅助元素，以使其使用成为可能？”
Eventually, the teacher may succeed in suggesting to the students the desirable idea. It consists in conceiving the diagonal of the given parallelepiped as the diagonal of a suitable parallelogram which must be introduced into the figure (as intersection of the parallelepiped with a plane passing through two opposite edges). The idea is essentially the same as before (section 10) but the approach is different. In section 10, the contact with the available knowledge of the students was established through the unknown; a formerly solved problem was recollected because its unknown was the same as that of the proposed problem. In the present section analogy provides the contact with the idea of the solution.
最终，教师可能会成功地向学生提出一个理想的想法。这包括将给定的平行四边形的对角线设想为一个合适的平行四边形的对角线，这个平行四边形必须被引入图形中（作为平行四边形与通过两个相对边缘的平面的交点）。这个想法与之前（第 10 节）基本相同，但方法不同。在第 10 节中，与学生现有知识的联系是通过未知数建立的；以前解决过的问题被回忆起来，因为它的未知数与建议的问题相同。在本节中，类比提供了与解决方案的想法的联系。
16. The teacher’s method of questioning shown in the foregoing sections 8, 10, 12, 14, 15 is essentially this: Begin with a general question or suggestion of our list, and, if necessary, come down gradually to more specific and concrete questions or suggestions till you reach one which elicits a response in the student’s mind. If you have to help the student exploit his idea, start again, if possible, from a general question or suggestion contained in the list, and return again to some more special one if necessary; and so on.
Of course, our list is just a first list of this kind; it seems to be sufficient for the majority of simple cases, but there is no doubt that it could be perfected. It is important, however, that the suggestions from which we start should be simple, natural, and general, and that their list should be short.
当然，我们的清单只是这种类型的第一份清单；它似乎足以满足大多数简单的情况，但毫无疑问，它可以得到完善。然而，重要的是，我们开始的建议应该是简单、自然和普遍的，而且它们的清单应该很短。
The suggestions must be simple and natural because otherwise they cannot be unobtrusive.
建议必须是简单和自然的，因为否则就无法做到不引人注目。
The suggestions must be general, applicable not only to the present problem but to problems of all sorts, if they are to help develop the ability of the student and not just a special technique.
这些建议必须是一般性的，不仅适用于目前的问题，而且适用于各种问题，如果它们有助于发展学生的能力，而不仅仅是一种特殊的技巧。
The list must be short in order that the questions may be often repeated, unartificially, and under varying circumstances; thus, there is a chance that they will be eventually assimilated by the student and will contribute to the development of a mental habit.
清单必须简短，以便在不同的情况下经常重复这些问题；这样，这些问题就有可能最终被学生所吸收，并有助于发展一种心理习惯。
It is necessary to come down gradually to specific suggestions, in order that the student may have as great a share of the work as possible.
为了让学生尽可能多地参与工作，有必要逐步提出具体建议。
This method of questioning is not a rigid one; fortunately so, because, in these matters, any rigid, mechanical, pedantical procedure is necessarily bad. Our method admits a certain elasticity and variation, it admits various approaches (section 15), it can be and should be so applied that questions asked by the teacher could have occurred to the student himself.
这种提问方法并不死板；幸好如此，因为在这些问题上，任何死板、机械、教条的程序都必然是不好的。我们的方法允许有一定的弹性和变化，允许有各种不同的方法（第 15 节），它可以而且应该这样应用，以至于老师提出的问题可以由学生自己想到。
If a reader wishes to try the method here proposed in his class he should, of course, proceed with caution. He should study carefully the example introduced in section 8, and the following examples in sections 18, 19, 20. He should prepare carefully the examples which he intends to discuss, considering also various approaches. He should start with a few trials and find out gradually how he can manage the method, how the students take it, and how much time it takes.
Let us go back to the situation as it presented itself at the beginning of section 10 when the question was asked: Do you know a related problem? Instead of this, with the best intention to help the students, the question may be offered: Could you apply the theorem of Pythagoras?
让我们回到第 10 节开始时提出的情况，当时的问题是这样的。你知道一个相关的问题吗？与此相反，本着帮助学生的良好愿望，可以提出这样的问题。你能运用毕达哥拉斯的定理吗？
The intention may be the best, but the question is about the worst. We must realize in what situation it was offered; then we shall see that there is a long sequence of objections against that sort of “help.”
其意图可能是最好的，但问题是关于最坏的。我们必须认识到这是在什么情况下提供的；然后我们将看到有一长串反对这种 “帮助” 的意见。
(1) If the student is near to the solution, he may understand the suggestion implied by the question; but if he is not, he quite possibly will not see at all the point at which the question is driving. Thus the question fails to help where help is most needed.
（1）如果学生接近解决方案，他可能会理解问题所暗示的建议；但如果他不是，他很可能根本看不到问题所指向的重点。因此，这个问题不能帮助最需要帮助的地方。
(2) If the suggestion is understood, it gives the whole secret away, very little remains for the student to do.
（2）如果这个建议被理解，它就会泄露整个秘密，留给学生的时间就很少了。
(3) The suggestion is of too special a nature. Even if the student can make use of it in solving the present problem, nothing is learned for future problems. The question is not instructive.
（3）该建议的性质过于特殊。即使学生能够利用它来解决目前的问题，也不能为将来的问题学到什么。这个问题不具有指导性。
(4) Even if he understands the suggestion, the student can scarcely understand how the teacher came to the idea of putting such a question. And how could he, the student, find such a question by himself? It appears as an unnatural surprise, as a rabbit pulled out of a hat; it is really not instructive.
（4）即使他理解了这个建议，学生也很难理解老师是如何想到提出这样一个问题的。而他，这个学生，又怎么能自己找到这样的问题呢？这似乎是一个不自然的惊喜，就像一只从帽子里掏出来的兔子；它真的不具有指导意义。
“What is the unknown?”
“未知的是什么？”
“A square.”
“一个正方形。”
“What are the data?”
“数据是什么？”
“A triangle is given, nothing else.”
“给了一个三角形，没有别的。”
“What is the condition?”
“是什么情况？”
“The four corners of the square should be on the perimeter of the triangle, two corners on the base, one corner on each of the other two sides.”
“正方形的四个角应该在三角形的周边，两个角在底座上，另外两个边上各有一个角。”
“Is it possible to satisfy the condition?”
“有可能满足这个条件吗？”
“I think so. I am not so sure.”
“我想是的。我不太确定。”
“You do not seem to find the problem too easy. If you cannot solve the proposed problem, try to solve first some related problem. Could you satisfy a part of the condition?”
“你似乎没有发现这个问题太容易。如果你不能解决所提出的问题，就先试着解决一些相关的问题。你能满足一部分的条件吗？”
“What do you mean by a part of the condition?”
“你说的条件的一部分是什么意思？”
“You see, the condition is concerned with all the vertices of the square. How many vertices are there?”
“你看，这个条件涉及到正方形的所有顶点。有多少个顶点？”
“Four.”
“四个。”
“A part of the condition would be concerned with less than four vertices. Keep only a part of the condition, drop the other part. What part of the condition is easy to satisfy?”
“条件的一部分会涉及到少于四个顶点的问题。只保留条件的一部分，放弃另一部分。条件的哪一部分容易满足？”
“It is easy to draw a square with two vertices on the perimeter of the triangle—or even one with three vertices on the perimeter!”
“在三角形的周长上画一个有两个顶点的正方形很容易，或者甚至在周长上画一个有三个顶点的正方形！”
“Draw a figure!”
“画个图吧！”
“You kept only a part of the condition, and you dropped the other part. How far is the unknown now determined?”
“你只保留了条件的一部分，而你放弃了另一部分。现在未知的东西确定到什么程度了？”
FIG. 2
图 2
“The square is not determined if it has only three vertices on the perimeter of the triangle.”
“如果在三角形的周长上只有三个顶点，那么这个正方形就不能确定。”
“Good! Draw a figure.”
“好!画个图吧。”
FIG. 3
图 3
“The square, as you said, is not determined by the part of the condition you kept. How can it vary?”
“正如你所说的，这个平方不是由你保持的那部分条件决定的。它怎么会有变化呢？”
. . . . .
…… . . .
. . . . .
…… . . .
“Try it experimentally, if you wish. Draw more squares with three corners on the perimeter in the same way as the two squares already in the figure. Draw small squares and large squares. What seems to be the locus of the fourth corner? How can it vary?”
“如果你愿意的话，可以通过实验来试试。在周边画更多有三个角的正方形，方法与图中已有的两个正方形相同。画小方块和大方块。第四角的位置似乎是什么？它可以如何变化？”
The teacher brought the student very near to the idea of the solution. If the student is able to guess that the locus of the fourth corner is a straight line, he has got it.
老师让学生非常接近解决的想法。如果学生能够猜出第四个角的位置是一条直线，他就得到了。
What we have to prove is a fundamental theorem of solid geometry. The problem may be proposed to students who are familiar with plane geometry and acquainted with those few facts of solid geometry which prepare the present theorem in Euclid’s Elements. (The theorem that we have stated and are going to prove is the proposition 10 of Book XI of Euclid.) Not only questions and suggestions quoted from our list are printed in italics but also others which correspond to them as “problems to prove” correspond to “problems to find.” (The correspondence is worked out systematically in PROBLEMS TO FIND, PROBLEMS TO PROVE 5, 6.)
我们要证明的是实体几何的一个基本定理。这个问题可以推荐给那些熟悉平面几何和熟悉实体几何的少数事实的学生，这些事实为欧几里得《元素》中的本定理做了准备。（我们所陈述和要证明的定理是欧几里德第十一卷的命题 10）。不仅从我们的清单中引用的问题和建议被印成斜体，而且与它们相对应的其他问题也被印成斜体，就像 “需要证明的问题” 与 “需要发现的问题” 相对应一样。（这种对应关系在《寻找的问题》、《证明的问题》5、6 中得到了系统的阐述）。
“What is the hypothesis?”
“假说是什么？”
“Two angles are in different planes. Each side of one is parallel to the corresponding side of the other, and has also the same direction.
"两个角是在不同的平面上。一个的每条边都与另一个的相应边平行，而且方向也相同。
“What is the conclusion?”
“结论是什么？”
“The angles are equal.”
“角度是相等的。”
“Draw a figure. Introduce suitable notation.”
“画一个图形。引入合适的符号。”
“What is the hypothesis? Say it, please, using your notation.”
“假说是什么？请说出来，用你的记号。”
“A, B, C are not in the same plane as A′, B′, C′. And AB || A′B′, AC || A′C′. Also AB has the same direction as A′B′, and AC the same as A′C′.”
“A、B、C与A′、B′、C′不在同一平面。而AB||A′B′，AC||A′C′。同时AB与A′B′方向相同，AC与A′C′方向相同。”
FIG. 4
图 4
“What is the conclusion?”
“结论是什么？”
“∠BAC = ∠B′A′C′.”
“∠bac=∠b′a′c′”。
“Look at the conclusion! And try to think of a familiar theorem having the same or a similar conclusion.”
“看看这个结论!试着想一想一个熟悉的定理有相同或类似的结论。”
“If two triangles are congruent, the corresponding angles are equal.”
“如果两个三角形全等，那么相应的角就相等。”
“Very good! Now here is a theorem related to yours and proved before. Could you use it?”
“非常好!现在这里有一个与你有关的定理，以前也证明过。你能用它吗？”
“I think so but I do not see yet quite how.”
“我想是的，但我还不太明白是怎么回事。”
“Should you introduce some auxiliary element in order to make its use possible?”
“你是否应该引入一些辅助元素，以使其使用成为可能？”
. . . . .
…… . . .
“No. But I could introduce some. Let me join B to C, and B′ to C′. Then there are two triangles, Δ ABC, Δ A′B′C′.”
“不，但我可以介绍一些。让我把B和C连接起来，把B′和C′连接起来。然后有两个三角形，ΔABC，ΔA′B′C′。”
“Well done. But what are these triangles good for?”
“做得好。但这些三角形有什么用？”
“To prove the conclusion, ∠BAC = ∠B′A′C′.”
“为了证明结论，∠BAC=∠B′A′C′。”
“Good! If you wish to prove this, what kind of triangles do you need?”
“好!如果你想证明这一点，你需要什么样的三角形？”
FIG. 5
图 5
“Congruent triangles. Yes, of course, I may choose B, C, B′, C′ so that
“共轭三角形。是的，当然，我可以选择B、C、B′、C′，以便
“Very good! Now, what do you wish to prove?”
“很好!现在，你想证明什么？”
“I wish to prove that the triangles are congruent,
"我希望证明这些三角形是全等的。
If I could prove this, the conclusion ∠BAC = ∠B′A′C′ would follow immediately.”
如果我能够证明这一点，结论∠BAC=∠B′A′C′将立即得出。"
“Two triangles are congruent if—if the three sides of the one are equal respectively to the three sides of the other.”
“如果一个三角形的三条边分别与另一个三角形的三条边相等，那么这两个三角形就是全等的。”
“Well done. You could have chosen a worse one. Now here is a theorem related to yours and proved before. Could you use it?”
“做得好。你可以选择一个更差的。现在这里有一个与你有关的定理，以前也证明过。你能用它吗？”
“I could use it if I knew that BC = B′C′.”
“如果我知道BC=B′C′，我就可以使用它。”
“That is right! Thus, what is your aim?”
“这就对了!因此，你的目的是什么？”
“To prove that BC = B′C′.”
“要证明BC=B′C′。”
“Try to think of a familiar theorem having the same or a similar conclusion.”
“试着想一想，一个熟悉的定理有相同或类似的结论。”
“Yes, I know a theorem finishing: ‘. . . then the two lines are equal.’ But it does not fit in.”
“是的，我知道一个定理整理：‘。. 那么这两条线是相等的’。但它并不适合。”
“Should you introduce some auxiliary element in order to make its use possible?”
“你是否应该引入一些辅助元素，以使其使用成为可能？”
. . . . .
…… . . .
“You see, how could you prove BC = B′C′ when there is no connection in the figure between BC and B′C′?”
“你看，图中BC和B′C′之间没有任何联系，你怎么能证明BC=B′C′ ？”
“Did you use the hypothesis? What is the hypothesis?”
“你用了假说吗？假设是什么？”
“We suppose that AB || A′B′, AC || A′C′. Yes, of course, I must use that.”
“我们假设AB||A′B′，AC||A′C′。是的，当然，我必须使用这个。”
“Did you use the whole hypothesis? You say that AB || A′B′. Is that all that you know about these lines?”
“你用了整个假说吗？你说AB||A′B′。这就是你对这些线的全部了解吗？”
“No; AB is also equal to A′B′, by construction. They are parallel and equal to each other. And so are AC and A′C′.”
“不；根据结构，AB也等于A′B′。它们是平行的，并且彼此相等。而AC和A′C′也是如此。”
“Two parallel lines of equal length—it is an interesting configuration. Have you seen it before?”
“两条等长的平行线 —— 这是个有趣的构造。你以前见过它吗？”
“Of course! Yes! Parallelogram! Let me join A to A′, B to B′, and C to C′.”
“当然！”。是的!平行四边形！让我把A连到A′，B连到B′，C连到 C′。"
“The idea is not so bad. How many parallelograms have you now in your figure?”
“这个想法并不坏。你现在的身材里有多少个平行四边形？”
We could have gathered from his foregoing answers that the student is intelligent. But after this last remark of his, there is no doubt.
我们可以从他前面的回答中得出结论，这个学生很聪明。但在他最后这句话之后，就没有疑问了。
This student is able to guess a mathematical result and to distinguish clearly between proof and guess. He knows also that guesses can be more or less plausible. Really, he did profit something from his mathematics classes; he has some real experience in solving problems, he can conceive and exploit a good idea.
这个学生能够猜测一个数学结果，并能明确区分证明和猜测。他还知道，猜测可能或多或少是可信的。事实上，他确实从数学课中获益匪浅；他有一些解决问题的实际经验，他能构思并利用一个好主意。
20. A rate problem. Water is flowing into a conical vessel at the rate r. The vessel has the shape of a right circular cone, with horizontal base, the vertex pointing downwards; the radius of the base is a, the altitude of the cone b. Find the rate at which the surface is rising when the depth of the water is y. Finally, obtain the numerical value of the unknown supposing that a = 4 ft., b = 3 ft., r = 2 cu. ft. per minute, and y = 1 ft.
FIG. 6
图 6
The students are supposed to know the simplest rules of differentiation and the notion of “rate of change.”
学生们应该知道最简单的微分规则和 “变化率” 的概念。
“What are the data?”
“数据是什么？”
“Correct. The statement of the problem seems to suggest that you should disregard, provisionally, the numerical values, work with the letters, express the unknown in terms of a, b, r, y and only finally, after having obtained the expression of the unknown in letters, substitute the numerical values. I would follow this suggestion. Now, what is the unknown?”
“正确。问题的陈述似乎表明，你应该暂时不考虑数值，用字母工作，用a、b、r、y来表达未知数，最后在得到未知数的字母表达后，才用数值代替。我将遵循这个建议。现在，未知数是什么？”
“The rate at which the surface is rising when the depth of the water is y.”
“当水的深度为y时，水面上升的速度。”
“What is that? Could you say it in other terms?”
“那是什么？你能用其他术语说吗？”
“The rate at which the depth of the water is increasing.”
“水的深度增加的速度”。
“What is that? Could you restate it still differently?”
“那是什么？你能不能用不同的方式重述一下？”
“The rate of change of the depth of the water.”
“水的深度的变化率”。
“That is right, the rate of change of y. But what is the rate of change? Go back to the definition.”
“没错，就是y的变化率。但什么是变化率？请回到定义。”
“The derivative is the rate of change of a function.”
“导数是一个函数的变化率”。
“Correct. Now, is y a function? As we said before, we disregard the numerical value of y. Can you imagine that y changes?”
“正确的。现在，y是一个函数吗？正如我们之前所说，我们不考虑y的数值，你能想象y的变化吗？”
“Yes, y, the depth of the water, increases as the time goes by.”
“是的，y，水的深度，随着时间的推移而增加。”
“Thus, y is a function of what?”
“因此，y是什么的函数？”
“Of the time t.”
“的时间T。”
“Good. Introduce suitable notation. How would you write the ‘rate of change of y’ in mathematical symbols?”
“好。介绍一下合适的符号。你会如何用数学符号写出 ‘y的变化率’？”
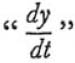
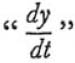
“Good. Thus, this is your unknown. You have to express it in terms of a, b, r, y. By the way, one of these data is a ‘rate.’ Which one?”
“很好。因此，这是你的未知数。你必须用a、b、r、y来表达它。顺便说一下，这些数据中有一个是 ‘速率’。哪一个？”
“What is that? Could you say it in other terms?”
“那是什么？你能用其他术语说吗？”
“r is the rate of change of the volume of the water in the vessel.”
“r是容器中水的体积的变化率。”
“What is that? Could you restate it still differently? How would you write it in suitable notation?”
“那是什么？你能以不同的方式重述它吗？你会如何用合适的记号来写？”
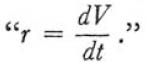
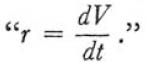
“What is V?”
“V是什么？”
“The volume of the water in the vessel at the time t.”
“在时间t，容器中的水的体积”。
“Good. Thus, you have to express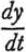 
in terms of a, b, 
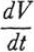, y. How will you do it?”
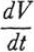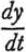“很好。因此，你必须用a, b,,y来表达 。你将如何做？”
. . . . .
…… . . .
“If you cannot solve the proposed problem try to solve first some related problem. If you do not see yet the connection between 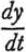and the data, try to bring in some simpler connection that could serve as a stepping stone.”
“如果你不能解决所提出的问题，试着先解决一些相关问题。如果你还没有看到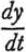 和数据之间的联系，试着引入一些更简单的联系，可以作为一个垫脚石。”
. . . . .
…… . . .
“Do you not see that there are other connections? For instance, are y and V independent of each other?”
“你没有看到还有其他的联系吗？例如，Y和V是相互独立的吗？”
“No. When y increases, V must increase too.”
“不，当y增加时，V也必须增加。”
“Thus, there is a connection. What is the connection?”
“因此，存在着一种联系。这种联系是什么？”
“Well, V is the volume of a cone of which the altitude is y. But I do not know yet the radius of the base.”
“嗯，V是高度为y的圆锥体的体积，但我还不知道底部的半径。”
“You may consider it, nevertheless. Call it something, say x.”
“尽管如此，你可以考虑一下。叫它什么，说是X。”
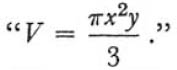
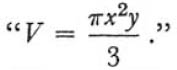
“Correct. Now, what about x? Is it independent of y?”
“正确的。现在，x 呢？它是独立于y 的吗？”
“No. When the depth of the water, y, increases the radius of the free surface, x, increases too.”
“不，当水的深度y增加时，自由表面的半径x也会增加。”
“Thus, there is a connection. What is the connection?”
“因此，存在着一种联系。这种联系是什么？”
“One more connection, you see. I would not miss profiting from it. Do not forget, you wished to know the connection between V and y.”
“还有一个联系，你看。我不会错过从中获利的机会。别忘了，你希望知道V和Y之间的联系。”
“I have
"我有
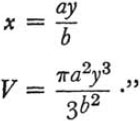
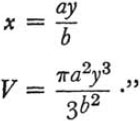
“Very good. This looks like a stepping stone, does it not? But you should not forget your goal. What is the unknown?”
“很好。这看起来像是一块垫脚石，不是吗？但你不应该忘记你的目标。未知是什么？”
“Well, .”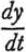
“嗯， 。”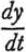
“You have to find a connection between 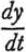, , 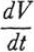and other quantities. And here you have one between y, V, and other quantities. What to do?”
“你必须找到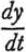 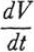， ，和其他数量之间的联系。而在这里你有一个y、V和其他数量之间的联系。怎么办？”
“Differentiate! Of course!
"差异化!当然了!
Here it is.”
就在这里。"
“Fine! And what about the numerical values?”
“很好！”。那么数值呢？"
“If a = 4, b = 3, = r = 2, y = 1, then
“如果a=4，b=3， =r=2，y=1，那么
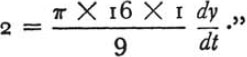
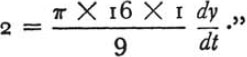
Where should I start? Start from the statement of the problem.
我应该从哪里开始？从问题的陈述开始。
What can I do? Visualize the problem as a whole as clearly and as vividly as you can. Do not concern yourself with details for the moment.
我可以做什么？尽可能清晰、生动地把问题看作一个整体。暂时不要关注细节。
What can I gain by doing so? You should understand the problem, familiarize yourself with it, impress its purpose on your mind. The attention bestowed on the problem may also stimulate your memory and prepare for the recollection of relevant points.
我这样做能得到什么？你应该理解这个问题，熟悉它，把它的目的印在你的脑海里。对问题的关注也可以刺激你的记忆，为回忆相关要点做准备。
Where should I start? Start again from the statement of the problem. Start when this statement is so clear to you and so well impressed on your mind that you may lose sight of it for a while without fear of losing it altogether.
我应该从哪里开始？再从问题的陈述开始。当这个陈述对你来说是如此清晰，并深深地印在你的脑海中，以至于你可以暂时忘记它而不必担心完全失去它时，再开始。
What can I do? Isolate the principal parts of your problem. The hypothesis and the conclusion are the principal parts of a “problem to prove”; the unknown, the data, and the conditions are the principal parts of a “problem to find.” Go through the principal parts of your problem, consider them one by one, consider them in turn, consider them in various combinations, relating each detail to other details and each to the whole of the problem.
我可以做什么？隔离你的问题的主要部分。假设和结论是 “需要证明的问题” 的主要部分；未知数、数据和条件是 “需要寻找的问题” 的主要部分。仔细研究你的问题的主要部分，一个一个地考虑，依次考虑，以不同的组合考虑，把每个细节与其他细节联系起来，每个细节与问题的整体联系起来。
Where should I start? Start from the consideration of the principal parts of your problem. Start when these principal parts are distinctly arranged and clearly conceived, thanks to your previous work, and when your memory seems responsive.
我应该从哪里开始？从考虑你的问题的主要部分开始。当这些主要部分已经有了明确的安排和清晰的构思，这要归功于你以前的工作，而且你的记忆力似乎很好的时候开始。
What can I do? Consider your problem from various sides and seek contacts with your formerly acquired knowledge.
我可以做什么？从各方面考虑你的问题，用你以前获得的知识寻求联系。
Consider your problem from various sides. Emphasize different parts, examine different details, examine the same details repeatedly but in different ways, combine the details differently, approach them from different sides. Try to see some new meaning in each detail, some new interpretation of the whole.
从不同侧面考虑你的问题。强调不同的部分，审视不同的细节，以不同的方式反复审视相同的细节，以不同的方式组合细节，从不同的侧面来看待它们。试着在每个细节中看到一些新的意义，对整体进行一些新的解释。
Seek contacts with your formerly acquired knowledge. Try to think of what helped you in similar situations in the past. Try to recognize something familiar in what you examine, try to perceive something useful in what you recognize.
用你以前获得的知识寻求联系。试着想一想，在过去类似的情况下，是什么帮助了你。试着从你检查的东西中认识到一些熟悉的东西，试着从你认识的东西中感知一些有用的东西。
What could I perceive? A helpful idea, perhaps a decisive idea that shows you at a glance the way to the very end.
我可以感知到什么？一个有帮助的想法，也许是一个决定性的想法，让你一目了然地看到通往最后的道路。
How can an idea be helpful? It shows you the whole of the way or a part of the way; it suggests to you more or less distinctly how you can proceed. Ideas are more or less complete. You are lucky if you have any idea at all.
一个想法怎么会有帮助呢？它向你展示了全部的方法或部分的方法；它或多或少明确地建议你如何进行。想法或多或少都是完整的。如果你有任何想法，你是幸运的。
What can I do with an incomplete idea? You should consider it. If it looks advantageous you should consider it longer. If it looks reliable you should ascertain how far it leads you, and reconsider the situation. The situation has changed, thanks to your helpful idea. Consider the new situation from various sides and seek contacts with your formerly acquired knowledge.
What can I gain by doing so again? You may be lucky and have another idea. Perhaps your next idea will lead you to the solution right away. Perhaps you need a few more helpful ideas after the next. Perhaps you will be led astray by some of your ideas. Nevertheless you should be grateful for all new ideas, also for the lesser ones, also for the hazy ones, also for the supplementary ideas adding some precision to a hazy one, or attempting the correction of a less fortunate one. Even if you do not have any appreciable new ideas for a while you should be grateful if your conception of the problem becomes more complete or more coherent, more homogeneous or better balanced.
我再这样做能得到什么？你可能很幸运，有另一个想法。也许你的下一个想法会让你马上找到解决方案。也许你在下一个想法之后还需要几个有用的想法。也许你会被你的一些想法带入歧途。然而，你应该感谢所有的新想法，也感谢那些较差的想法，也感谢那些朦胧的想法，也感谢那些为朦胧的想法增加一些精确性的补充想法，或试图纠正一个不太幸运的想法。即使你暂时没有任何可观的新想法，如果你对问题的概念变得更完整或更连贯，更均匀或更平衡，你也应该感谢。
Where should I start? Start from the lucky idea that led you to the solution. Start when you feel sure of your grasp of the main connection and you feel confident that you can supply the minor details that may be wanting.
我应该从哪里开始？从引导你找到解决方案的幸运想法开始。当你确信你掌握了主要的联系，并且你感到有信心能够提供可能需要的小细节时，就开始吧。
What can I do? Make your grasp quite secure. Carry through in detail all the algebraic or geometric operations which you have recognized previously as feasible. Convince yourself of the correctness of each step by formal reasoning, or by intuitive insight, or both ways if you can. If your problem is very complex you may distinguish “great” steps and “small” steps, each great step being composed of several small ones. Check first the great steps, and get down to the smaller ones afterwards.
我可以做什么？使你的掌握相当安全。把你以前认为可行的所有代数或几何运算详细地进行一遍。通过正式的推理，或通过直观的洞察力，或通过这两种方式（如果你能做到的话）来说服自己相信每一步的正确性。如果你的问题非常复杂，你可以区分 “大” 步骤和 “小” 步骤，每个大步骤都由几个小步骤组成。首先检查大步骤，然后再检查小步骤。
What can I gain by doing so? A presentation of the solution each step of which is correct beyond doubt.
我这样做能得到什么？对解决方案的介绍，其中每一步都是正确无误的。
Where should I start? From the solution, complete and correct in each detail.
我应该从哪里开始？从解决方案开始，在每个细节上都要完整和正确。
What can I do? Consider the solution from various sides and seek contacts with your formerly acquired knowledge.
我可以做什么？从各方面考虑解决方案，用你以前获得的知识寻求联系。
Consider the details of the solution and try to make them as simple as you can; survey more extensive parts of the solution and try to make them shorter; try to see the whole solution at a glance. Try to modify to their advantage smaller or larger parts of the solution, try to improve the whole solution, to make it intuitive, to fit it into your formerly acquired knowledge as naturally as possible. Scrutinize the method that led you to the solution, try to see its point, and try to make use of it for other problems. Scrutinize the result and try to make use of it for other problems.
考虑解决方案的细节，并试图使它们尽可能简单；调查解决方案中更广泛的部分，并试图使它们更短；试图一目了然地看到整个解决方案。尝试修改解决方案中较小或较大的部分，使其具有优势，尝试改进整个解决方案，使其具有直观性，尽可能自然地融入你以前获得的知识。仔细研究导致你找到解决方案的方法，试着看清它的意义，并试着将它用于其他问题。仔细检查结果，并尝试将其用于其他问题。
What can I gain by doing so? You may find a new and better solution, you may discover new and interesting facts. In any case, if you get into the habit of surveying and scrutinizing your solutions in this way, you will acquire some knowledge well ordered and ready to use, and you will develop your ability of solving problems.
我这样做能获得什么？你可能会发现一个新的和更好的解决方案，你可能会发现新的和有趣的事实。无论如何，如果你养成了以这种方式调查和检查你的解决方案的习惯，你将获得一些井然有序、随时可用的知识，你也将发展你解决问题的能力。
1. A rectangular parallelogram is analogous to a rectangular parallelepiped. In fact, the relations between the sides of the parallelogram are similar to those between the faces of the parallelepiped:
1. 矩形平行四边形与矩形平行四边形相类似。事实上，平行四边形各边之间的关系与平行四边形各面之间的关系相似。
Each side of the parallelogram is parallel to just one other side, and is perpendicular to the remaining sides.
平行四边形的每条边只与另一条边平行，并与其余的边垂直。
Each face of the parallelepiped is parallel to just one other face, and is perpendicular to the remaining faces.
平行四边形的每个面只与另一个面平行，而与其余的面垂直。
Let us agree to call a side a “bounding element” of the parallelogram and a face a “bounding element” of the parallelepiped. Then, we may contract the two foregoing statements into one that applies equally to both figures:
让我们同意把一个边称为平行四边形的 “边界元素”，而把一个面称为平行四边形的 “边界元素”。然后，我们可以将上述两个声明收缩为一个声明，同样适用于这两个图形。
Each bounding element is parallel to just one other bounding element and is perpendicular to the remaining bounding elements.
每个界线元素只与另一个界线元素平行，并与其余界线元素垂直。
Thus, we have expressed certain relations which are common to the two systems of objects we compared, sides of the rectangle and faces of the rectangular parallelepiped. The analogy of these systems consists in this community of relations.
因此，我们已经表达了某些关系，这些关系是我们所比较的两个物体系统所共有的，即矩形的边和矩形平行四边形的面。这些系统的类比包括这个关系的共同体。
2. Analogy pervades all our thinking, our everyday speech and our trivial conclusions as well as artistic ways of expression and the highest scientific achievements. Analogy is used on very different levels. People often use vague, ambiguous, incomplete, or incompletely clarified analogies, but analogy may reach the level of mathematical precision. All sorts of analogy may play a role in the discovery of the solution and so we should not neglect any sort.
3. We may consider ourselves lucky when, trying to solve a problem, we succeed in discovering a simpler analogous problem. In section 15, our original problem was concerned with the diagonal of a rectangular parallelepiped; the consideration of a simpler analogous problem, concerned with the diagonal of a rectangle, led us to the solution of the original problem. We are going to discuss one more case of the same sort. We have to solve the following problem:
3. 当我们试图解决一个问题时，我们可以认为自己很幸运，因为我们成功地发现了一个更简单的类似问题。在第 15 节中，我们最初的问题是关于一个矩形平行四边形的对角线；考虑一个更简单的类似问题，即关于一个矩形的对角线，使我们找到了最初问题的解决方案。我们将讨论另一个类似的案例。我们必须解决以下问题。
Find the center of gravity of a homogeneous tetrahedron.
找出一个同质四面体的重心。
Without knowledge of the integral calculus, and with little knowledge of physics, this problem is not easy at all; it was a serious scientific problem in the days of Archimedes or Galileo. Thus, if we wish to solve it with as little preliminary knowledge as possible, we should look around for a simpler analogous problem. The corresponding problem in the plane occurs here naturally:
如果没有积分微积分的知识，而且没有什么物理学知识，这个问题一点也不容易；在阿基米德或伽利略的时代，这是一个严重的科学问题。因此，如果我们希望以尽可能少的初步知识来解决它，我们应该四处寻找一个更简单的类似问题。平面上的相应问题在这里自然而然地出现了。
Find the center of gravity of a homogeneous triangle.
找出一个同质三角形的重心。
Now, we have two questions instead of one. But two questions may be easier to answer than just one question—provided that the two questions are intelligently connected.
现在，我们有两个问题而不是一个。但是，两个问题可能比一个问题更容易回答 —— 只要这两个问题有智慧的联系。
4. Laying aside, for the moment, our original problem concerning the tetrahedron, we concentrate upon the simpler analogous problem concerning the triangle. To solve this problem, we have to know something about centers of gravity. The following principle is plausible and presents itself naturally.
4. 暂且不说我们原来关于四面体的问题，我们专注于关于三角形的更简单的类似问题。为了解决这个问题，我们必须了解一些关于重心的知识。下面的原则是可信的，而且是自然而然地提出来的。
This principle yields all that we need in the case of the triangle. First, it implies that the center of gravity of the triangle lies in the plane of the triangle. Then, we may consider the triangle as consisting of fibers (thin strips, “infinitely narrow” parallelograms) parallel to a certain side of the triangle (the side AB in Fig. 7). The center of gravity of each fiber (of any parallelogram) is, obviously, its midpoint, and all these midpoints lie on the line joining the vertex C opposite to the side AB to the midpoint M of AB (see Fig. 7).
FIG. 7
图 7
Any plane passing through the median CM of the triangle contains the centers of gravity of all parallel fibers which constitute the triangle. Thus, we are led to the conclusion that the center of gravity of the whole triangle lies on the same median. Yet it must lie on the other two medians just as well, it must be the common point of intersection of all three medians.
任何通过三角形中线的平面都包含构成三角形的所有平行纤维的重心。因此，我们可以得出结论，整个三角形的重心位于同一个中线上。然而，它也必须位于另外两条中线上，它必须是所有三条中线的共同交点。
It is desirable to verify now by pure geometry, independently of any mechanical assumption, that the three medians meet in the same point.
现在最好通过纯粹的几何学来验证，独立于任何机械的假设，这三个中线在同一点上相遇。
In solving the analogous problem which we use now as a model, we conceived the triangle ABC as consisting of fibers parallel to one of its sides, AB. Now, we conceive the tetrahedron ABCD as consisting of fibers parallel to one of its edges, AB.
在解决我们现在用作模型的类似问题时，我们将三角形ABC设想为由平行于其一条边AB的纤维组成。现在，我们将四面体ABCD设想为由平行于其一条边AB的纤维组成。
The midpoints of the fibers which constitute the triangle lie all on the same straight line, a median of the triangle, joining the midpoint M of the side AB to the opposite vertex C. The midpoints of the fibers which constitute the tetrahedron lie all in the same plane, joining the midpoint M of the edge AB to the opposite edge CD (see Fig. 8); we may call this plane MCD a median plane of the tetrahedron.
构成三角形的纤维的中点都位于同一条直线上，这是三角形的中线，连接边AB的中点M和对面的顶点C。构成四面体的纤维的中点都位于同一个平面内，连接边AB的中点M和对面的边CD（见图 8）；我们可以把这个平面MCD称为四面体的中线平面。
FIG. 8
图 8
In the case of the triangle, we had three medians like MC, each of which has to contain the center of gravity of the triangle. Therefore, these three medians must meet in one point which is precisely the center of gravity. In the case of the tetrahedron we have six median planes like MCD, joining the midpoint of some edge to the opposite edge, each of which has to contain the center of gravity of the tetrahedron. Therefore, these six median planes must meet in one point which is precisely the center of gravity.
6. Thus, we have solved the problem of the center of gravity of the homogeneous tetrahedron. To complete our solution, it is desirable to verify now by pure geometry, independently of mechanical considerations, that the six median planes mentioned pass through the same point.
6. 因此，我们已经解决了同质四面体的重心问题。为了完成我们的解决方案，现在最好通过纯粹的几何学来验证，独立于机械方面的考虑，所述的六个中线平面通过同一个点。
When we had solved the problem of the center of gravity of the homogeneous triangle, we found it desirable to verify, in order to complete our solution, that the three medians of the triangle pass through the same point. This problem is analogous to the foregoing but visibly simpler.
当我们解决了同质三角形的重心问题后，我们发现为了完成我们的解决方案，最好验证一下三角形的三条中线是否通过同一点。这个问题与前述问题类似，但明显更简单。
Again we may use, in solving the problem concerning the tetrahedron, the simpler analogous problem concerning the triangle (which we may suppose here as solved). In fact, consider the three median planes, passing through the three edges DA, DB, DC issued from the vertex D; each passes also through the midpoint of the opposite edge (the median plane through DC passes through M, see Fig. 8). Now, these three median planes intersect the plane of Δ ABC in the three medians of this triangle. These three medians pass through the same point (this is the result of the simpler analogous problem) and this point, just as D, is a common point of the three median planes. The straight line, joining the two common points, is common to all three median planes.
在解决关于四面体的问题时，我们可以再次使用关于三角形的更简单的类似问题（我们在此可以假设它已被解决）。事实上，考虑三个中线平面，分别通过从顶点D发出的三条边DA、DB、DC；每个中线平面也通过对面边的中点（通过DC的中线平面通过M，见图 8）。现在，这三个中线平面与ΔABC的平面相交于这个三角形的三个中线。这三个中线通过同一点（这是更简单的类比问题的结果），这一点和D一样，是三个中线平面的公共点。连接这两个公共点的直线是所有三个中线平面的共同点。
We proved that those 3 among the 6 median planes which pass through the vertex D have a common straight line. The same must be true of those 3 median planes which pass through A; and also of the 3 median planes through B; and also of the 3 through C. Connecting these facts suitably, we may prove that the 6 median planes have a common point. (The 3 median planes passing through the sides of Δ ABC determine a common point, and 3 lines of intersection which meet in the common point. Now, by what we have just proved, through each line of intersection one more median plane must pass.)
7. Both under 5 and under 6 we used a simpler analogous problem, concerning the triangle, to solve a problem about the tetrahedron. Yet the two cases are different in an important respect. Under 5, we used the method of the simpler analogous problem whose solution we imitated point by point. Under 6, we used the result of the simpler analogous problem, and we did not care how this result had been obtained. Sometimes, we may be able to use both the method and the result of the simpler analogous problem. Even our foregoing example shows this if we regard the considerations under 5 and 6 as different parts of the solution of the same problem.
7. 在第 5 条和第 6 条下，我们都用一个更简单的类似问题，即关于三角形的问题，来解决关于四面体的问题。然而，这两种情况在一个重要方面是不同的。在第 5 项下，我们使用了较简单的类比问题的方法，我们逐点模仿了其解决方案。在第 6 种情况下，我们使用了更简单的类比问题的结果，而我们并不关心这个结果是如何得到的。有时，我们可以同时使用较简单类比问题的方法和结果。如果我们把 5 和 6 下的考虑视为同一问题解决方案的不同部分，甚至我们前面的例子也表明了这一点。
Our example is typical. In solving a proposed problem, we can often use the solution of a simpler analogous problem; we may be able to use its method, or its result, or both. Of course, in more difficult cases, complications may arise which are not yet shown by our example. Especially, it can happen that the solution of the analogous problem cannot be immediately used for our original problem. Then, it may be worth while to reconsider the solution, to vary and to modify it till, after having tried various forms of the solution, we find eventually one that can be extended to our original problem.
我们的例子很典型。在解决一个提议的问题时，我们往往可以使用一个更简单的类似问题的解决方案；我们可能会使用它的方法，或者它的结果，或者两者都使用。当然，在更困难的情况下，可能会出现我们的例子中还没有显示的复杂情况。特别是，可能发生的情况是，类似问题的解决方案不能立即用于我们的原始问题。那么，可能值得重新考虑解决方案，改变和修改它，直到在尝试了各种形式的解决方案之后，我们最终找到一个可以扩展到我们原来的问题。
8. It is desirable to foresee the result, or, at least, some features of the result, with some degree of plausibility. Such plausible forecasts are often based on analogy.
8. 最好能在一定程度上可信地预见结果，或至少预见结果的某些特征。这种似是而非的预测往往是以类比为基础的。
Thus, we may know that the center of gravity of a homogeneous triangle coincides with the center of gravity of its three vertices (that is, of three material points with equal masses, placed in the vertices of the triangle). Knowing this, we may conjecture that the center of gravity of a homogeneous tetrahedron coincides with the center of gravity of its four vertices.
This conjecture is an “inference by analogy.” Knowing that the triangle and the tetrahedron are alike in many respects, we conjecture that they are alike in one more respect. It would be foolish to regard the plausibility of such conjectures as certainty, but it would be just as foolish, or even more foolish, to disregard such plausible conjectures.
这种猜想是一种 “类比推理”。我们知道三角形和四面体在许多方面都是一样的，所以我们猜测它们在另一个方面也是一样的。将这种猜想的合理性视为确定性是愚蠢的，但无视这种合理的猜想也是同样愚蠢的，甚至是更愚蠢的。
Inference by analogy appears to be the most common kind of conclusion, and it is possibly the most essential kind. It yields more or less plausible conjectures which may or may not be confirmed by experience and stricter reasoning. The chemist, experimenting on animals in order to foresee the influence of his drugs on humans, draws conclusions by analogy. But so did a small boy I knew. His pet dog had to be taken to the veterinary, and he inquired:
类比推理似乎是最常见的一种结论，也可能是最基本的一种。它产生了或多或少可信的猜想，这些猜想可能被经验和更严格的推理所证实，也可能不被证实。化学家在动物身上做实验，以预见他的药物对人类的影响，通过类比得出结论。但我认识的一个小男孩也是这样。他的宠物狗不得不被带到兽医那里，他询问道。
“Who is the veterinary?”
“谁是兽医？”
“The animal doctor.”
“动物医生”。
“Which animal is the animal doctor?”
“哪个动物是动物医生？”
9. An analogical conclusion from many parallel cases is stronger than one from fewer cases. Yet quality is still more important here than quantity. Clear-cut analogies weigh more heavily than vague similarities, systematically arranged instances count for more than random collections of cases.
9. 从许多平行案例中得出的类比结论比从较少的案例中得出的结论要强。然而，质量在这里仍然比数量更重要。明确的类比比模糊的相似性更重要，系统地安排的实例比随机收集的实例更重要。
In the foregoing (under 8) we put forward a conjecture about the center of gravity of the tetrahedron. This conjecture was supported by analogy; the case of the tetrahedron is analogous to that of the triangle. We may strengthen the conjecture by examining one more analogous case, the case of a homogeneous rod (that is, a straight line-segment of uniform density).
The analogy between
之间的类比
has many aspects. A segment is contained in a straight line, a triangle in a plane, a tetrahedron in space. Straight line-segments are the simplest one-dimensional bounded figures, triangles the simplest polygons, tetrahedrons the simplest polyhedrons.
有许多方面。一个线段包含在一条直线上，一个三角形包含在一个平面上，一个四面体包含在空间里。直线段是最简单的一维有界图形，三角形是最简单的多边形，四面体是最简单的多面体。
The segment has 2 zero-dimensional bounding elements (2 end-points) and its interior is one-dimensional.
该段有 2 个零维的边界元素（2 个端点），其内部是一维的。
The triangle has 3 zero-dimensional and 3 one-dimensional bounding elements (3 vertices, 3 sides) and its interior is two-dimensional.
三角形有 3 个零维和 3 个一维的边界元素（3 个顶点，3 条边），其内部是二维的。
The tetrahedron has 4 zero-dimensional, 6 one-dimensional, and 4 two-dimensional bounding elements (4 vertices, 6 edges, 4 faces), and its interior is three-dimensional.
四面体有 4 个零维、6 个一维和 4 个二维的边界元素（4 个顶点、6 条边、4 个面），其内部是三维的。
These numbers can be assembled into a table. The successive columns contain the numbers for the zero-, one-, two-, and three-dimensional elements, the successive rows the numbers for the segment, triangle, and tetrahedron:
这些数字可以组合成一个表格。连续的列包含零、一、二和三维元素的数字，连续的行包含线段、三角形和四面体的数字。
Very little familiarity with the powers of a binomial is needed to recognize in these numbers a section of Pascal’s triangle. We found a remarkable regularity in segment, triangle, and tetrahedron.
几乎不需要熟悉二项式的幂，就可以从这些数字中认出帕斯卡三角形的一段。我们发现段、三角形和四面体都有显著的规律性。
10. If we have experienced that the objects we compare are closely connected, “inferences by analogy,” as the following, may have a certain weight with us.
10. 如果我们有经验，我们比较的对象是密切相关的，那么像下面这样的 “类比推论” 可能对我们有一定的分量。
The center of gravity of a homogeneous rod coincides with the center of gravity of its 2 end-points. The center of gravity of a homogeneous triangle coincides with the center of gravity of its 3 vertices. Should we not suspect that the center of gravity of a homogeneous tetrahedron coincides with the center of gravity of its 4 vertices?
Again, the center of gravity of a homogeneous rod divides the distance between its end-points in the proportion 1 : 1. The center of gravity of a triangle divides the distance between any vertex and the midpoint of the opposite side in the proportion 2 : 1. Should we not suspect that the center of gravity of a homogeneous tetrahedron divides the distance between any vertex and the center of gravity of the opposite face in the proportion 3: 1?
同样，同质杆的重心是以 1：1 的比例划分其端点之间的距离。三角形的重心以 2：1 的比例划分任何顶点和对边中点之间的距离。我们难道不应该怀疑同质四面体的重心以 3：1 的比例划分任何顶点和对边重心之间的距离吗？
It appears extremely unlikely that the conjectures suggested by these questions should be wrong, that such a beautiful regularity should be spoiled. The feeling that harmonious simple order cannot be deceitful guides the discoverer both in the mathematical and in the other sciences, and is expressed by the Latin saying: simplex sigillum veri (simplicity is the seal of truth).
这些问题所提出的猜想似乎极不可能是错误的，如此美丽的规则性应该被破坏。和谐的简单秩序不可能是欺骗性的，这种感觉在数学和其他科学中都指导着发现者，并以拉丁语的说法来表达：simplex sigillum veri（简单是真理的印记）。
[The preceding suggests an extension to n dimensions. It appears unlikely that what is true in the first three dimensions, for n = 1, 2, 3, should cease to be true for higher values of n. This conjecture is an “inference by induction”; it illustrates that induction is naturally based on analogy. See INDUCTION AND MATHEMATICAL INDUCTION.]
前面的内容表明可以扩展到n 个维度。在前三个维度中，对于n=1、2、3 来说是真的，对于更高的n值来说，似乎不太可能不再是真的。这个猜想是一个 “归纳推理”；它说明了归纳法自然是基于类比的。见归纳法和数学归纳法。
[11. We finish the present section by considering briefly the most important cases in which analogy attains the precision of mathematical ideas.
[11. 在本节的最后，我们简要地考虑一下最重要的案例，在这些案例中，类比达到了数学思想的精确度。
(I) Two systems of mathematical objects, say S and S′, are so connected that certain relations between the objects of S are governed by the same laws as those between the objects of S′.
（I）两个数学对象系统，例如S和S′，是这样连接的：S的对象之间的某些关系是由S′的对象之间的相同规律所支配。
(II) There is a one-one correspondence between the objects of the two systems S and S′, preserving certain relations. That is, if such a relation holds between the objects of one system, the same relation holds between the corresponding objects of the other system. Such a connection between two systems is a very precise sort of analogy; it is called isomorphism (or holohedral isomorphism).
（二）两个系统的对象S和S′之间存在着一一对应的关系，保留了某些关系。也就是说，如果这种关系在一个系统的对象之间成立，那么同样的关系在另一个系统的相应对象之间也成立。两个系统之间的这种联系是一种非常精确的类比；它被称为同构（或全能同构）。
(III) There is a one-many correspondence between the objects of the two systems S and S′ preserving certain relations. Such a connection (which is important in various branches of advanced mathematical study, especially in the Theory of Groups, and need not be discussed here in detail) is called merohedral isomorphism (or homomorphism; homoiomorphism would be, perhaps, a better term). Merohedral isomorphism may be considered as another very precise sort of analogy.]
（III）在两个系统的对象S和S′之间存在着保留某些关系的一目了然的对应关系。这种联系（在高级数学研究的各个分支中，特别是在群论中很重要，在此不必详细讨论）被称为 merohedral 同构（或同构；同构也许是一个更好的术语）。中面体同构可以被看作是另一种非常精确的类比。］
Auxiliary elements. There is much more in our conception of the problem at the end of our work than was in it as we started working (PROGRESS AND ACHIEVEMENT, 1). As our work progresses, we add new elements to those originally considered. An element that we introduce in the hope that it will further the solution is called an auxiliary element.
1. There are various kinds of auxiliary elements. Solving a geometric problem, we may introduce new lines into our figure, auxiliary lines. Solving an algebraic problem, we may introduce an auxiliary unknown (AUXILIARY PROBLEMS, 1). An auxiliary theorem is a theorem whose proof we undertake in the hope of promoting the solution of our original problem.
1. 有各种类型的辅助元素。解决一个几何问题，我们可以在我们的图形中引入新的线条，即辅助线。解决一个代数问题，我们可以引入一个辅助的未知数（AUXILIARY PROBLEMS，1）。辅助定理是一个我们进行证明的定理，希望能促进我们原始问题的解决。
2. There are various reasons for introducing auxiliary elements. We are glad when we have succeeded in recollecting a problem related to ours and solved before. It is probable that we can use such a problem but we do not know yet how to use it. For instance, the problem which we are trying to solve is a geometric problem, and the related problem which we have solved before and have now succeeded in recollecting is a problem about triangles. Yet there is no triangle in our figure; in order to make any use of the problem recollected we must have a triangle; therefore, we have to introduce one, by adding suitable auxiliary lines to our figure. In general, having recollected a formerly solved related problem and wishing to use it for our present one, we must often ask: Should we introduce some auxiliary element in order to make its use possible? (The example in section 10 is typical.)
Going back to definitions, we have another opportunity to introduce auxiliary elements. For instance, explicating the definition of a circle we should not only mention its center and its radius, but we should also introduce these geometric elements into our figure. Without introducing them, we could not make any concrete use of the definition; stating the definition without drawing something is mere lip-service.
回到定义上，我们又有机会引入辅助元素。例如，在阐释圆的定义时，我们不仅应该提到它的中心和半径，而且还应该把这些几何元素引入我们的图形中。如果不引入这些元素，我们就无法具体使用这个定义；只说定义而不画东西，只是口惠而实不至。
Trying to use known results and going back to definitions are among the best reasons for introducing auxiliary elements; but they are not the only ones. We may add auxiliary elements to the conception of our problem in order to make it fuller, more suggestive, more familiar although we scarcely know yet explicitly how we shall be able to use the elements added. We may just feel that it is a “bright idea” to conceive the problem that way with such and such elements added.
试图使用已知的结果和回到定义是引入辅助元素的最佳理由之一；但它们不是唯一的理由。我们可以在问题的概念中加入辅助元素，以便使它更全面、更有提示性、更熟悉，尽管我们几乎不清楚我们将如何使用所加入的元素。我们可能只是觉得，用这样那样的元素来构思问题是一个 “聪明的想法”。
3. Example. Construct a triangle, being given one angle, the altitude drawn from the vertex of the given angle, and the perimeter of the triangle.
3.例子。构建一个三角形，给定一个角，从给定的角的顶点出发的高度，以及三角形的周长。
FIG. 9
图 9
FIG. 10
图 10
We introduce suitable notation. Let α denote the given angle, h the given altitude drawn from the vertex A of α and p the given perimeter. We draw a figure in which we easily place α and h. Have we used all the data? No, our figure does not contain the given length p, equal to the perimeter of the triangle. Therefore we must introduce p. But how?
In fact, the triangle has three unknown sides a, b, c. We call a, as usual, the side opposite to A; we know that
事实上，三角形有三条未知的边a、b、c。我们像往常一样把a称为与A相对的边；我们知道
Now, the sides b and c play the same role; they are interchangeable; our problem is symmetric with respect to b and c. But b and c do not play the same role in our figures 9, 10; placing the length p we treated b and c differently; the figures 9 and 10 spoil the natural symmetry of the problem with respect to b and c. We should place p so that it has the same relation to b as to c.
This consideration may be helpful in suggesting to place the length p as in Fig. 11. We add to the side a of
这种考虑可能有助于建议像图 11那样放置长度p。我们在a的边上加上
FIG. 11
图 11
the triangle the segment CE of length b on one side and the segment BD of the length c on the other side so that p appears in Fig. 11 as the line ED of length
三角形的一边是长为b的线段CE，另一边是长为c的线段BD，所以图 11中的P是长为ED的线。
If we have some little experience in solving problems of construction, we shall not fail to introduce into the figure, along with ED, the auxiliary lines AD and AE, each of which is the base of an isosceles triangle. In fact, it is not unreasonable to introduce elements into the problem which are particularly simple and familiar, as isosceles triangle.
We have been quite lucky in introducing our auxiliary lines. Examining the new figure we may discover that ∠EAD has a simple relation to the given angle α. In fact, we find using the isosceles triangles Δ ABD and Δ ACE that ∠DAE =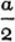 
+ 90°. After this remark, it is natural to try the construction of Δ DAE. Trying this construction, we introduce an auxiliary problem which is much easier than the original problem.
在引入我们的辅助线时，我们已经相当幸运了。检查新的图形，我们可能会发现∠EAD与给定的角度α有一个简单的关系。事实上，我们用等腰三角形ΔABD和ΔACE发现，∠DAE=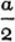 +90°。在这句话之后，很自然地要尝试构建ΔDAE。在尝试这一构造时，我们引入了一个辅助问题，它比原问题要简单得多。
4. Teachers and authors of textbooks should not forget that the intelligent student and THE INTELLIGENT READER are not satisfied by verifying that the steps of a reasoning are correct but also want to know the motive and the purpose of the various steps. The introduction of an auxiliary element is a conspicuous step. If a tricky auxiliary line appears abruptly in the figure, without any motivation, and solves the problem surprisingly, intelligent students and readers are disappointed; they feel that they are cheated. Mathematics is interesting in so far as it occupies our reasoning and inventive powers. But there is nothing to learn about reasoning and invention if the motive and purpose of the most conspicuous step remain incomprehensible. To make such steps comprehensible by suitable remarks (as in the foregoing, under 3) or by carefully chosen questions and suggestions (as in sections 10, 18, 19, 20) takes a lot of time and effort; but it may be worth while.
4. 教师和教科书的作者不应忘记，聪明的学生和聪明的读者并不满足于验证推理的步骤是否正确，他们还想知道各个步骤的动机和目的。辅助元素的引入是一个显眼的步骤。如果一个棘手的辅助线突然出现在图中，没有任何动机，而且出人意料地解决了问题，聪明的学生和读者就会感到失望；他们觉得自己被骗了。数学之所以有趣，是因为它占用了我们的推理和发明能力。但是，如果最明显的步骤的动机和目的仍然是不可理解的，那么推理和发明就没有什么可学的。通过适当的评论（如前面的第 3 节）或通过精心选择的问题和建议（如第 10、18、19、20 节）使这些步骤变得容易理解，需要花费很多时间和精力；但这可能是值得的。
An insect tries to escape through the windowpane, tries the same again and again, and does not try the next window which is open and through which it came into the room. A man is able, or at least should be able, to act more intelligently. Human superiority consists in going around an obstacle that cannot be overcome directly, in devising a suitable auxiliary problem when the original problem appears insoluble. To devise an auxiliary problem is an important operation of the mind. To raise a clear-cut new problem subservient to another problem, to conceive distinctly as an end what is means to another end, is a refined achievement of the intelligence. It is an important task to learn (or to teach) how to handle auxiliary problems intelligently.
一只昆虫试图通过窗玻璃逃跑，一次又一次地尝试同样的方法，而不去尝试它进入房间的下一扇打开着的窗户。人能够，或者至少应该能够，更明智地采取行动。人的优越性在于绕过无法直接克服的障碍，在于当原始问题似乎无法解决时，设计出一个合适的辅助问题。设计一个辅助问题是思维的一个重要操作。提出一个明确的、服从于另一个问题的新问题，将一个目的明确地设想为另一个目的的手段，是智力的一个高雅成就。学习（或教导）如何智能地处理辅助问题是一项重要的任务。
1. Example. Find x, satisfying the equation
1.例子。求x，满足方程
If we observe that x4 = (x2)2 we may see the advantage of introducing
如果我们观察到x4=（x2）2，我们可能会看到引入的好处
We obtain now a new problem: Find y, satisfying the equation
我们现在得到一个新的问题：找到满足方程的y
The new problem is an auxiliary problem; we intend to use it as a means of solving our original problem. The unknown of our auxiliary problem, y, is appropriately called auxiliary unknown.
这个新问题是一个辅助问题；我们打算把它作为解决我们原始问题的手段。我们的辅助问题的未知数，y，被恰当地称为辅助未知数。
2. Example. Find the diagonal of a rectangular parallelepiped being given the lengths of three edges drawn from the same corner.
2.例子。给出从同一角出发的三条边的长度，求一个长方形平行四边形的对角线。
The new problem is an auxiliary problem; we consider it because we hope to derive some profit for the original problem from its consideration.
新问题是一个辅助问题；我们考虑它是因为我们希望从它的考虑中获得一些原始问题的利润。
3. Profit. The profit that we derive from the consideration of an auxiliary problem may be of various kinds. We may use the result of the auxiliary problem. Thus, in example 1, having found by solving the quadratic equation for y that y is equal to 4 or to 9, we infer that x2 = 4 or x2 = 9 and derive hence all possible values of x. In other cases, we may use the method of the auxiliary problem. Thus, in example 2, the auxiliary problem is a problem of plane geometry; it is analogous to, but simpler than, the original problem which is a problem of solid geometry. It is reasonable to introduce an auxiliary problem of this kind in the hope that it will be instructive, that it will give us opportunity to familiarize ourselves with certain methods, operations, or tools, which we may use afterwards for our original problem. In example 2, the choice of the auxiliary problem is rather lucky; examining it closely we find that we can use both its method and its result. (See section 15, and DID YOU USE ALL THE DATA?)
3.利润。我们从对一个辅助问题的考虑中获得的利润可能有各种类型。我们可以使用辅助问题的结果。因此，在例 1 中，通过解决y的二次方程发现y等于 4 或等于 9，我们推断x2=4 或x2=9，并由此得出x的所有可能值。因此，在例 2 中，辅助问题是一个平面几何问题；它与原始问题类似，但比原始问题更简单，后者是一个实体几何问题。引入这类辅助问题是合理的，因为我们希望它是有启发性的，它将使我们有机会熟悉某些方法、操作或工具，这些方法、操作或工具我们以后可能用于我们的原始问题。在例 2 中，辅助问题的选择是相当幸运的；仔细研究它，我们发现我们可以同时使用它的方法和结果。（见第 15 节，以及你是否使用了所有的数据？）
4. Risk. We take away from the original problem the time and the effort that we devote to the auxiliary problem. If our investigation of the auxiliary problem fails, the time and effort we devoted to it may be lost. Therefore, we should exercise our judgment in choosing an auxiliary problem. We may have various good reasons for our choice. The auxiliary problem may appear more accessible than the original problem; or it may appear instructive; or it may have some sort of aesthetic appeal. Sometimes the only advantage of the auxiliary problem is that it is new and offers unexplored possibilities; we choose it because we are tired of the original problem all approaches to which seem to be exhausted.
5. How to find one. The discovery of the solution of the proposed problem often depends on the discovery of a suitable auxiliary problem. Unhappily, there is no infallible method of discovering suitable auxiliary problems as there is no infallible method of discovering the solution. There are, however, questions and suggestions which are frequently helpful, as LOOK AT THE UNKNOWN. We are often led to useful auxiliary problems by VARIATION OF THE PROBLEM.
5.如何找到一个。所提出问题的解决方案的发现往往取决于合适的辅助问题的发现。不幸的是，没有无懈可击的方法来发现合适的辅助问题，就像没有无懈可击的方法来发现解决方案一样。然而，有一些问题和建议经常是有帮助的，就像“观察未知”。我们经常通过问题的变化来引导我们找到有用的辅助性问题。
6. Equivalent problems. Two problems are equivalent if the solution of each involves the solution of the other. Thus, in our example 1, the original problem and the auxiliary problem are equivalent.
6.等价问题。如果两个问题的解决都涉及到另一个问题的解决，那么它们就是等价的。因此，在我们的例子 1 中，原始问题和辅助问题是等同的。
Consider the following theorems:
请考虑以下定理。
A. In any equilateral triangle, each angle is equal to 60°.
A·在任何等边三角形中，每个角都等于 60°。
B. In any equiangular triangle, each angle is equal to 60°.
B·在任何等边三角形中，每个角都等于 60°。
These two theorems are not identical. They contain different notions; one is concerned with equality of the sides, the other with equality of the angles of a triangle. But each theorem follows from the other. Therefore, the problem to prove A is equivalent to the problem to prove B.
这两个定理并不完全相同。它们包含不同的概念；一个是关于边的平等，另一个是关于三角形的角的平等。但每个定理都是由另一个定理引出的。因此，证明 A 的问题等同于证明 B 的问题。
If we are required to prove A, there is a certain advantage in introducing, as an auxiliary problem, the problem to prove B. The theorem B is a little easier to prove than A and, what is more important, we may foresee that B is easier than A, we may judge so, we may find plausible from the outset that B is easier than A. In fact, the theorem B, concerned only with angles, is more “homogeneous” than the theorem A which is concerned with both angles and sides.
The passage from the original problem to the auxiliary problem is called convertible reduction, or bilateral reduction, or equivalent reduction if these two problems, the original and the auxiliary, are equivalent. Thus, the reduction of A to B (see above) is convertible and so is the reduction in example 1. Convertible reductions are, in a certain respect, more important and more desirable than other ways to introduce auxiliary problems, but auxiliary problems which are not equivalent to the original problem may also be very useful; take example 2.
如果原始问题和辅助问题这两个问题是等价的，那么从原始问题到辅助问题的通道被称为可转换还原，或双边还原，或等价还原。因此，从 A 到 B 的还原（见上文）是可转换的，例 1 中的还原也是如此。在某种程度上，可转换还原比其他引入辅助问题的方式更重要、更理想，但与原问题不等价的辅助问题也可能非常有用；以例 2 为例。
7. Chains of equivalent auxiliary problems are frequent in mathematical reasoning. We are required to solve a problem A; we cannot see the solution, but we may find that A is equivalent to another problem B. Considering B we may run into a third problem C equivalent to B. Proceeding in the same way, we reduce C to D, and so on, until we come upon a last problem L whose solution is known or immediate. Each problem being equivalent to the preceding, the last problem L must be equivalent to our original problem A. Thus we are able to infer the solution of the original problem A from the problem L which we attained as the last link in a chain of auxiliary problems.
7.等价辅助问题链在数学推理中经常出现。我们被要求解决一个问题 A；我们看不到解决方案，但我们可能发现 A 与另一个问题 B 是等价的。考虑到 B，我们可能会遇到与 B 等价的第三个问题 C。以同样的方式进行，我们将 C 还原为 D，以此类推，直到我们遇到最后一个问题 L，其解决方案是已知的或直接的。每个问题都等同于前面的问题，最后一个问题 L 一定等同于我们最初的问题 A。因此，我们能够从问题 L 中推断出最初问题 A 的解决方案，而问题 L 是我们获得的辅助问题链的最后一环。
Chains of problems of this kind were noticed by the Greek mathematicians as we may see from an important passage of PAPPUS. For an illustration, let us reconsider our example 1. Let us call (A) the condition imposed upon the unknown x:
希腊数学家注意到了这种问题链，我们可以从PAPPUS的一个重要段落看到。为了说明问题，让我们重新考虑一下我们的例子 1。让我们称（A）为强加给未知数x的条件。
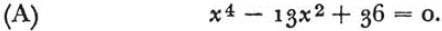
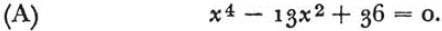
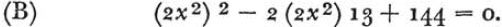
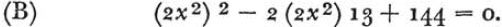
Observe that the conditions (A) and (B) are different. They are only slightly different if you wish to say so, they are certainly equivalent as you may easily convince yourself, but they are definitely not identical. The passage from (A) to (B) is not only correct but has a clear-cut purpose, obvious to anybody who is familiar with the solution of quadratic equations. Working further in the same direction we transform the condition (B) into still another condition (C) :
请注意，条件（A）和（B）是不同的。如果你想这么说的话，它们只是略有不同，它们当然是等价的，因为你可以很容易地说服自己，但它们绝对不是相同的。从（A）到（B）的段落不仅是正确的，而且有一个明确的目的，对任何熟悉二次方程解法的人来说都是明显的。沿着同一方向进一步努力，我们将条件（B）转化为另一个条件（C）。
Proceeding in the same way, we obtain
以同样的方式进行，我们得到
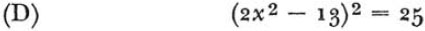
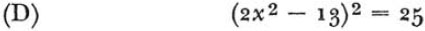
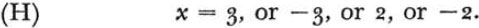
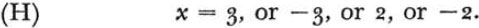
Each reduction that we made was convertible. Thus, the last condition (H) is equivalent to the first condition (A) so that 3, −3, 2, −2 are all possible solutions of our original equation.
我们所做的每个还原都是可以转换的。因此，最后一个条件（H）等同于第一个条件（A），所以 3、-3、2、-2 都是我们原始方程的可能解。
In the foregoing we derived from an original condition (A) a sequence of conditions (B), (C), (D), . . . each of which was equivalent to the foregoing. This point deserves the greatest care. Equivalent conditions are satisfied by the same objects. Therefore, if we pass from a proposed condition to a new condition equivalent to it, we have the same solutions. But if we pass from a proposed condition to a narrower one, we lose solutions, and if we pass to a wider one we admit improper, adventitious solutions which have nothing to do with the proposed problem. If, in a series of successive reductions, we pass to a narrower and then again to a wider condition we may lose track of the original problem completely. In order to avoid this danger, we must check carefully the nature of each newly introduced condition: Is it equivalent to the original condition? This question is still more important when we do not deal with a single equation as here but with a system of equations, or when the condition is not expressed by equations as, for instance, in problems of geometric construction.
在前文中，我们从一个原始条件（A）推导出一连串的条件（B）、（C）、（D）、…… ，其中每一个都与前文等价。这一点值得高度重视。等价的条件是由相同的对象满足的。因此，如果我们从一个提议的条件传递到一个与之等价的新条件，我们就会有相同的解决方案。但是，如果我们从一个提议的条件转到一个更窄的条件，我们就会失去解决方案，如果我们转到一个更宽的条件，我们就会接受不恰当的、偶然的解决方案，这些解决方案与提议的问题毫无关系。如果在一系列连续的还原中，我们转到一个更窄的条件，然后再转到一个更宽的条件，我们可能会完全失去对原始问题的追踪。为了避免这种危险，我们必须仔细检查每个新引入的条件的性质。它是否等同于原来的条件？当我们不是像这里一样处理一个单一的方程，而是处理一个方程组时，或者当条件不是由方程来表达时，例如在几何结构问题中，这个问题就更加重要。
(Compare PAPPUS, especially comments 2, 3, 4, 8. The description on p. 143, lines 4–21, is unnecessarily restricted; it describes a chain of “problems to find,” each of which has a different unknown. The example considered here has just the opposite speciality: all problems of the chain have the same unknown and differ only in the form of the condition. Of course, no such restriction is necessary.)
（比较PAPPUS，特别是评论 2、3、4、8）。第 143 页第 4-21 行的描述是不必要的限制；它描述了一连串的 “要找的问题”，其中每个问题都有不同的未知数。这里考虑的例子正好有相反的特点：这一连串的问题都有相同的未知数，只在条件的形式上有所不同。当然，这种限制是没有必要的）。
8. Unilateral reduction. We have two problems, A and B, both unsolved. If we could solve A we could hence derive the full solution of B. But not conversely; if we could solve B, we would obtain, possibly, some information about A, but we would not know how to derive the full solution of A from that of B. In such a case, more is achieved by the solution of A than by the solution of B. Let us call A the more ambitious, and B the less ambitious of the two problems.
8.单边还原。我们有两个问题，A 和 B，都没有解决。如果我们能解决 A，我们就能推导出 B 的全部解决方案。但不是反过来；如果我们能解决 B，我们将获得，可能，关于 A 的一些信息，但我们不知道如何从 B 的解决方案中推导出 A 的全部解决方案。
Our example 2 shows a unilateral reduction to a less ambitious problem. In fact, if we could solve the original problem, concerned with a parallelepiped whose length, width, and height are a, b, c respectively, we could move on to the auxiliary problem putting c = 0 and obtaining a parallelogram with length a and width b. For another example of a unilateral reduction to a less ambitious problem see SPECIALIZATION, 3, 4, 5. These examples show that, with some luck, we may be able to use a less ambitious auxiliary problem as a stepping stone, combining the solution of the auxiliary problem with some appropriate supplementary remark to obtain the solution of the original problem.
我们的例子 2 显示了对一个不太雄心勃勃的问题的单边还原。事实上，如果我们能解决原问题，即一个长、宽、高分别为a、b、c的平行四边形，我们就可以继续解决辅助问题，将c=0，得到一个长a、宽b的平行四边形。这些例子表明，如果运气好的话，我们也许可以用一个不太雄心勃勃的辅助问题作为垫脚石，将辅助问题的解决与一些适当的补充说明结合起来，得到原问题的解决。
Unilateral reduction to a more ambitious problem may also be successful. (See GENERALIZATION, 2, and the reduction of the first to the second problem considered in INDUCTION AND MATHEMATICAL INDUCTION, 1, 2.) In fact, the more ambitious problem may be more accessible; this is the INVENTOR’S PARADOX.
单方面还原到一个更宏大的问题也可能是成功的。（见GENERALIZATION，2，以及在INDUCTION 和 MATHEMATICAL INDUCTION，1，2 中考虑的第一个问题到第二个问题的还原。）事实上，更雄心勃勃的问题可能更容易得到；这就是发明家的范式。
Bolzano, Bernard (1781-1848), logician and mathematician, devoted an extensive part of his comprehensive presentation of logic, Wissenschaftslehre, to the subject of heuristic (vol. 3, pp. 293-575). He writes about this part of his work: “I do not think at all that I am able to present here any procedure of investigation that was not perceived long ago by all men of talent; and I do not promise at all that you can find here anything quite new of this kind. But I shall take pains to state in clear words the rules and ways of investigation which are followed by all able men, who in most cases are not even conscious of following them. Although I am free from the illusion that I shall fully succeed even in doing this, I still hope that the little that is presented here may please some people and have some application afterwards.”
Bright idea, or “good idea,” or “seeing the light,” is a colloquial expression describing a sudden advance toward the solution; see PROGRESS AND ACHIEVEMENT, 6. The coming of a bright idea is an experience familiar to everybody but difficult to describe and so it may be interesting to notice that a very suggestive description of it has been incidentally given by an authority as old as Aristotle.
Most people will agree that conceiving a bright idea is an “act of sagacity.” Aristotle defines “sagacity” as follows: “Sagacity is a hitting by guess upon the essential connection in an inappreciable time. As for example, if you see a person talking with a rich man in a certain way, you may instantly guess that that person is trying to borrow money. Or observing that the bright side of the moon is always toward the sun, you may suddenly perceive why this is; namely, because the moon shines by the light of the sun.”1
大多数人都会同意，构思一个聪明的想法是一种 “贤明的行为”。亚里士多德对 “智慧” 的定义如下。“狡猾是指在不可估量的时间内，通过猜测击中本质的联系。例如，如果你看到一个人以某种方式与一个富人交谈，你可能立即猜到那个人是想借钱。或者观察到月亮明亮的一面总是朝向太阳，你可能会突然意识到这是为什么；即因为月亮是由太阳的光照耀的。1
The first example is not bad but rather trivial; not much sagacity is needed to guess things of this sort about rich men and money, and the idea is not very bright. The second example, however, is quite impressive if we make a little effort of imagination to see it in its proper setting.
第一个例子并不坏，但相当琐碎；猜测这种关于富人和金钱的事情并不需要太多的智慧，而且这个想法也不是很光明。然而，如果我们稍微努力想象一下，在适当的环境中看到它，第二个例子就会令人印象深刻。
We should realize that a contemporary of Aristotle had to watch the sun and the stars if he wished to know the time since there were no wristwatches, and had to observe the phases of the moon if he planned traveling by night since there were no street lights. He was much better acquainted with the sky than the modern city-dweller, and his natural intelligence was not dimmed by undigested fragments of journalistic presentations of astronomical theories. He saw the full moon as a flat disc, similar to the disc of the sun but much less bright. He must have wondered at the incessant changes in the shape and position of the moon. He observed the moon occasionally also at daytime, about sunrise or sunset, and found out “that the bright side of the moon is always toward the sun” which was in itself a respectable achievement. And now he perceives that the varying aspects of the moon are like the various aspects of a ball which is illuminated from one side so that one half of it is shiny and the other half dark. He conceives the sun and the moon not as flat discs but as round bodies, one giving and the other receiving the light. He understands the essential connection, he rearranges his former conceptions instantly, “in an inappreciable time”: there is a sudden leap of the imagination, a bright idea, a flash of genius.
我们应该认识到，亚里士多德的同代人如果想知道时间，就必须观察太阳和星星，因为当时没有手表，如果他计划在夜间旅行，就必须观察月相，因为当时没有路灯。他比现代的城市居民更熟悉天空，，他的自然智慧并没有因为新闻界对天文理论的介绍的未消化的碎片而黯淡。他看到满月是一个平坦的圆盘，与太阳的圆盘相似，但亮度要低得多。他一定对月亮的形状和位置的不断变化感到奇怪。他偶尔也在白天观察月亮，大约在日出或日落时分，发现 “月亮明亮的一面总是朝着太阳”，这本身就是一个值得尊敬的成就。现在他意识到，月亮的不同方面就像一个球的不同方面，这个球从一侧被照亮，所以它的一半是光亮的，另一半是黑暗的。他认为太阳和月亮不是扁平的圆盘，而是圆形的身体，一个发出光，另一个接受光。他理解了这种基本的联系，他立即重新安排了他以前的概念，“在一个不可估量的时间内”：有一个突然的想象力的飞跃，一个明亮的想法，一个天才的闪光。
1. Numerical results of mathematical problems can be tested by comparing them to observed numbers, or to a commonsense estimate of observable numbers. As problems arising from practical needs or natural curiosity almost always aim at facts it could be expected that such comparisons with observable facts are seldom omitted. Yet every teacher knows that students achieve incredible things in this respect. Some students are not disturbed at all when they find 16,130 ft. for the length of the boat and 8 years, 2 months for the age of the captain who is, by the way, known to be a grandfather. Such neglect of the obvious does not show necessarily stupidity but rather indifference toward artificial problems.
2. Problems “in letters” are susceptible of more, and more interesting, tests than “problems in numbers” (section 14). For another example, let us consider the frustum of a pyramid with square base. If the side of the lower base is a, the side of the upper base b, and the altitude of the frustum h, we find for the volume
2. 与 “数字问题”（第 14 节）相比，“字母” 问题容易受到更多、更有趣的测试。另一个例子是，让我们考虑一个正方形底的金字塔的外壳。如果下底的边为a，上底的边为 b，壳的高度为h，我们可以发现体积为
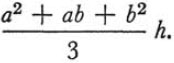
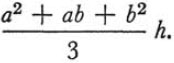
We may test this result by SPECIALIZATION. In fact, if b = a the frustum becomes a prism and the formula yields a2h; and if b = 0 the frustum becomes a pyramid and the formula yields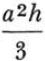 
. We may apply the TEST BY DIMENSION. In fact, the expression has as dimension the cube of a length. Again, we may test the formula by variation of the data. In fact, if any one of the positive quantities a, b or h increases the value of the expression increases.
我们可以通过特殊化来检验这个结果。事实上，如果b=a，地壳就变成了棱柱，公式得到的是a2h；如果b=0，地壳就变成了金字塔，公式得到的是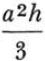 。我们可以应用TEST BY DIMENSION的方法。事实上，这个表达式的维度是长度的立方。同样，我们可以通过数据的变化来测试这个公式。事实上，如果任何一个正量a、b或h增加，表达式的值就会增加。
Tests of this sort can be applied not only to the final result but also to intermediate results. They are so useful that it is worth while preparing for them; see VARIATION OF THE PROBLEM, 4. In order to be able to use such tests, we may find advantage in generalizing a “problem in numbers” and changing it into a “problem in letters”; see GENERALIZATION, 3.
这类测试不仅可以应用于最终结果，也可以应用于中间结果。为了能够使用这种测试，我们可能会发现将 “数字问题” 归纳为 “字母问题” 的好处；见归纳，3。
3. Can you check the argument? Checking the argument step by step, we should avoid mere repetition. First, mere repetition is apt to become boring, uninstructive, a strain on the attention. Second, where we stumbled once, there we are likely to stumble again if the circumstances are the same as before. If we feel that it is necessary to go again through the whole argument step by step, we should at least change the order of the steps, or their grouping, to introduce some variation.
4. It requires less exertion and is more interesting to pick out the weakest point of the argument and examine it first. A question very useful in picking out points of the argument that are worth while examining is: DID YOU USE ALL THE DATA?
4. 挑选出论证中最薄弱的一点并首先对其进行研究，需要花费的精力较少，也更有意义。在挑选出值得研究的论点方面，一个非常有用的问题是。你使用了所有的数据吗？
5. It is clear that our nonmathematical knowledge cannot be based entirely on formal proofs. The more solid part of our everyday knowledge is continually tested and strengthened by our everyday experience. Tests by observation are more systematically conducted in the natural sciences. Such tests take the form of careful experiments and measurements, and are combined with mathematical reasoning in the physical sciences. Can our knowledge in mathematics be based on formal proofs alone?
5. 很明显，我们的非数学知识不可能完全建立在形式证明上。我们日常知识中比较扎实的部分是通过我们的日常经验不断检验和加强的。在自然科学中，通过观察进行的检验是比较系统的。这种测试采取仔细的实验和测量的形式，并在物理科学中与数学推理相结合。我们在数学方面的知识是否可以仅仅基于形式上的证明？
This is a philosophical question which we cannot debate here. It is certain that your knowledge, or my knowledge, or your students’ knowledge in mathematics is not based on formal proofs alone. If there is any solid knowledge at all, it has a broad experimental basis, and this basis is broadened by each problem whose result is successfully tested.
这是一个哲学问题，我们不能在这里辩论。可以肯定的是，你的知识，或我的知识，或你学生的数学知识，都不是仅仅基于形式上的证明。如果有任何扎实的知识，它都有广泛的实验基础，而这个基础又因每个问题的结果被成功检验而扩大。
Can you derive the result differently? When the solution that we have finally obtained is long and involved, we naturally suspect that there is some clearer and less roundabout solution: Can you derive the result differently? Can you see it at a glance? Yet even if we have succeeded in finding a satisfactory solution we may still be interested in finding another solution. We desire to convince ourselves of the validity of a theoretical result by two different derivations as we desire to perceive a material object through two different senses. Having found a proof, we wish to find another proof as we wish to touch an object after having seen it.
Two proofs are better than one. “It is safe riding at two anchors.”
两个证明比一个好。“在两个锚上骑行是安全的。”
1. Example. Find the area S of the lateral surface of the frustum of a right circular cone, being given the radius of the lower base R, the radius of the upper base r, and the altitude h.
1.例子。给出下底的半径R，上底的半径r和高度h，求一个直角圆锥体的侧面面积S。
This problem can be solved by various procedures. For instance, we may know the formula for the lateral surface of a full cone. As the frustum is generated by cutting off from a cone a smaller cone, so its lateral surface is the difference of two full conical surfaces; it remains to express these in terms of R, r, h. Carrying through this idea, we obtain finally the formula
这个问题可以通过各种程序来解决。例如，我们可以知道一个全圆锥体的侧向表面的公式。由于圆锥体是通过从一个圆锥体上切下一个较小的圆锥体而产生的，所以它的侧表面是两个全圆锥体表面之差；剩下的就是用R、r、h来表示这些。
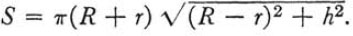
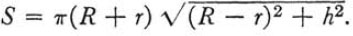
Having found this result in some way or other, after longer calculation, we may desire a clearer and less roundabout argument. Can you derive the result differently? Can you see it at a glance?
在以某种方式找到这个结果后，经过较长时间的计算，我们可能希望有一个更清晰、更不迂回的论证。你能以不同的方式得出这个结果吗？你能一目了然地看到它吗？
Desiring to see intuitively the whole result, we may begin with trying to see the geometric meaning of its parts. Thus, we may observe that
希望直观地看到整个结果，我们可以从尝试看到其部分的几何意义开始。因此，我们可以观察到
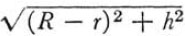
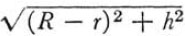
is the length of the slant height. (The slant height is one of the nonparallel sides of the isosceles trapezoid that, revolving about the line joining the midpoints of its parallel sides, generates the frustum; see Fig. 12.) Again, we may discover that
是斜面高度的长度。（斜高是等腰梯形的非平行边之一，它围绕连接其平行边中点的线旋转，产生了壳；见图 12）。同样，我们可以发现
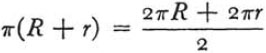
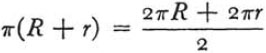
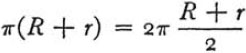
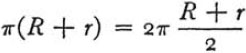
that is the perimeter of the mid-section of the frustum. (We call here mid-section the intersection of the frustum with a plane which is parallel both to the lower base and to the upper base of the frustum and bisects the altitude.)
这是该果壳中段的周长。（我们在此称中段为地壳与一个平面的交点，该平面既平行于地壳的下底，也平行于地壳的上底，并且将高度一分为二。）
FIG. 12
图 12
Having found new interpretations of various parts, we may see now the whole formula in a different light. We may read it thus:
在发现了对各部分的新解释之后，我们现在可以从不同的角度来看待整个公式。我们可以这样解读它。
We may recall here the rule for the trapezoid:
在此我们可以回顾一下梯形的规则。
(The middle-line is parallel to the two parallel sides of the trapezoid and bisects the altitude.) Seeing intuitively the analogy of both statements, that about the frustum and that about the trapezoid, we see the whole result about the frustum “almost at a glance.” That is, we feel that we are very near now to a short and direct proof of the result found by a long calculation.
2. The foregoing example is typical. Not entirely satisfied with our derivation of the result, we wish to improve it, to change it. Therefore, we study the result, trying to understand it better, to see some new aspect of it. We may succeed first in observing a new interpretation of a certain small part of the result. Then, we may be lucky enough to discover some new mode of conceiving some other part.
2. 前面的例子是典型的。我们对自己推导出的结果并不完全满意，我们希望改进它，改变它。因此，我们研究这个结果，试图更好地理解它，看到它的某些新方面。我们可能首先成功地观察到对结果的某一小部分的新解释。然后，我们可能会幸运地发现一些构想其他部分的新模式。
Examining the various parts, one after the other, and trying various ways of considering them, we may be led finally to see the whole result in a different light, and our new conception of the result may suggest a new proof.
一个接一个地检查各个部分，并尝试各种考虑它们的方式，我们最终可能会被引导到从不同的角度看待整个结果，而我们对结果的新概念可能会提出一个新的证明。
It may be confessed that all this is more likely to happen to an experienced mathematician dealing with some advanced problem than to a beginner struggling with some elementary problem. The mathematician who has a great deal of knowledge is more exposed than the beginner to the danger of mobilizing too much knowledge and framing an unnecessarily involved argument. But, as a compensation, the experienced mathematician is in a better position than the beginner to appreciate the reinterpretation of a small part of the result and to proceed, accumulating such small advantages, to recasting ultimately the whole result.
可以承认的是，这一切更有可能发生在处理一些高级问题的有经验的数学家身上，而不是发生在为一些初级问题奋斗的初学者身上。拥有大量知识的数学家比初学者更有可能调动过多的知识，形成不必要的争论。但是，作为一种补偿，有经验的数学家比初学者更容易理解对结果的一小部分的重新解释，并在积累这种小的优势后，最终重新铸造整个结果。
Nevertheless, it can happen even in very elementary classes that the students present an unnecessarily complicated solution. Then, the teacher should show them, at least once or twice, not only how to solve the problem more shortly but also how to find, in the result itself, indications of a shorter solution.
然而，即使在非常初级的课堂上，也可能发生学生提出一个不必要的复杂解决方案。这时，老师应该告诉他们，至少一次或两次，不仅要告诉他们如何更快解决问题，还要告诉他们如何在结果本身中找到更短的解决方案。
See also REDUCTIO AD ABSURDUM AND INDIRECT PROOF.
另见REDUCTIO AD ABSURDUM 和 INDIRECT PROOF。
Can you use the result? To find the solution of a problem by our own means is a discovery. If the problem is not difficult, the discovery is not so momentous, but it is a discovery nevertheless. Having made some discovery, however modest, we should not fail to inquire whether there is something more behind it, we should not miss the possibilities opened up by the new result, we should try to use again the procedure used. Exploit your success! Can you use the result, or the method, for some other problem?
1. We can easily imagine new problems if we are somewhat familiar with the principal means of varying a problem, as GENERALIZATION, SPECIALIZATION, ANALOGY, DECOMPOSING AND RECOMBINING. We start from a proposed problem, we derive from it others by the means we just mentioned, from the problems we obtained we derive still others, and so on. The process is unlimited in theory but, in practice, we seldom carry it very far, because the problems that we obtain so are apt to be inaccessible.
1. 如果我们对改变一个问题的主要方法有一定的了解，如通用化、专门化、模拟、分解和再混合，我们就可以很容易地想象出新的问题。我们从一个提议的问题开始，通过我们刚才提到的方法从这个问题推导出其他问题，从我们得到的问题中推导出其他问题，如此反复。这个过程在理论上是无限的，但在实践中，我们很少能走得很远，因为我们所得到的问题很可能是无法得到的。
On the other hand we can construct new problems which we can easily solve using the solution of a problem previously solved; but these easy new problems are apt to be uninteresting.
另一方面，我们可以构建新的问题，利用以前解决的问题的解决方案，我们可以很容易地解决这些问题；但这些容易的新问题很可能是无趣的。
To find a new problem which is both interesting and accessible, is not so easy; we need experience, taste, and good luck. Yet we should not fail to look around for more good problems when we have succeeded in solving one. Good problems and mushrooms of certain kinds have something in common; they grow in clusters. Having found one, you should look around; there is a good chance that there are some more quite near.
要找到一个既有趣又容易的新问题并不容易；我们需要经验、品味和好运气。然而，当我们成功地解决了一个问题后，我们不应该不四处寻找更多的好问题。好问题和某些类型的蘑菇有共同之处；它们成群结队地生长。找到一个之后，你应该四处看看；很有可能附近还有一些。
2. We are going to illustrate some of the foregoing points by the same example that we discussed in sections 8, 10, 12, 14, 15. Thus we start from the following problem:
2. 我们将通过我们在第 8、10、12、14、15 节中讨论的同一个例子来说明前述的一些观点。因此，我们从以下问题开始。
Given the three dimensions (length, breadth, and height) of a rectangular parallelepiped, find the diagonal.
给出一个长方形平行四边形的三个维度（长、宽、高），求其对角线。
Given the three dimensions of a rectangular parallelepiped, find the radius of the circumscribed sphere.
给出一个矩形平行四边形的三个维度，求圆周球体的半径。
The base of a pyramid is a rectangle of which the center is the foot of the altitude of the pyramid. Given the altitude of the pyramid and the sides of its base, find the lateral edges.
一个金字塔的底座是一个长方形，其中心是金字塔的高度的脚。给出金字塔的高度和底座的边，找出侧边。
Given the rectangular coordinates (x1, y1, z1), (x2, y2, z2) of two points in space, find the distance of these points.
给出空间中两点的矩形坐标（x1，y1，z1），（x2，y2，z2），求这些点的距离。
We solve these problems easily because they are scarcely different from the original problem whose solution we know. In each case, we add some new notion to our original problem, as circumscribed sphere, pyramid, rectangular coordinates. These notions are easily added and easily eliminated, and, having got rid of them, we fall back upon our original problem.
我们很容易解决这些问题，因为它们与我们已知的原始问题的解决方案几乎没有什么不同。在每一种情况下，我们都会给我们的原始问题添加一些新的概念，如圆周球、金字塔、矩形坐标。这些概念很容易添加，也很容易消除，摆脱了这些概念之后，我们又回到了原来的问题上。
The foregoing problems have a certain interest because the notions that we introduced into the original problem are interesting. The last problem, that about the distance of two points given by their coordinates, is even an important problem because rectangular coordinates are important.
上述问题有一定的意义，因为我们引入到原始问题中的概念是有趣的。最后一个问题，即关于由坐标给出的两点的距离，甚至是一个重要的问题，因为矩形坐标很重要。
3. Here is another problem which we can easily solve if we know the solution of our original problem: Given the length, the breadth, and the diagonal of a rectangular parallelepiped, find the height.
3. 下面是另一个问题，如果我们知道原问题的答案，就可以轻松解决：给定一个长方形平行四边形的长、宽和对角线，求其高度。
In fact, the solution of our original problem consists essentially in establishing a relation among four quantities, the three dimensions of the parallelepiped and its diagonal. If any three of these four quantities are given, we can calculate the fourth from the relation. Thus, we can solve the new problem.
事实上，我们最初问题的解决主要是在四个量之间建立一种关系，即平行四边形的三个维度和它的对角线。如果这四个量中的任何三个被给定，我们可以从关系中计算出第四个。因此，我们可以解决这个新问题。
We have here a pattern to derive easily solvable new problems from a problem we have solved: we regard the original unknown as given and one of the original data as unknown. The relation connecting the unknown and the data is the same in both problems, the old and the new. Having found this relation in one, we can use it also in the other.
This pattern of deriving new problems by interchanging the roles is very different from the pattern followed under 2.
这种通过互换角色而产生新问题的模式与 2 下的模式非常不同。
4. Let us now derive some new problems by other means.
4. 现在让我们通过其他方式推导出一些新问题。
A natural generalization of our original problem is the following: Find the diagonal of a parallelepiped, being given the three edges issued from an end-point of the diagonal, and the three angles between these three edges.
我们最初问题的一个自然概括是如下。给出从对角线的一个端点发出的三条边，以及这三条边之间的三个角，求平行四边形的对角线。
By specialization we obtain the following problem: Find the diagonal of a cube with given edge.
通过特殊化，我们得到以下问题：找到一个有给定边的立方体的对角线。
We may be led to an inexhaustible variety of problems by analogy. Here are a few derived from those considered under 2: Find the diagonal of a regular octahedron with given edge. Find the radius of the circumscribed sphere of a regular tetrahedron with given edge. Given the geographical coordinates, latitude and longitude, of two points on the earth’s surface (which we regard as a sphere) find their spherical distance.
通过类比，我们可能会被引导到各种取之不尽的问题。下面是一些从第 2 章中考虑的问题衍生出来的问题：求一个有给定边的正八面体的对角线。求一个有给定边的正四面体的圆周半径。给出地球表面两点（我们认为是一个球体）的地理坐标，即经度和纬度，求其球面距离。
All these problems are interesting but only the one obtained by specialization can be solved immediately on the basis of the solution of the original problem.
所有这些问题都很有趣，但只有通过专业化得到的问题可以在解决原始问题的基础上立即得到解决。
5. We may derive new problems from a proposed one by considering certain of its elements as variable.
5. 我们可以通过将某些元素视为变量，从拟议的问题中得出新的问题。
A special case of a problem mentioned under 2 is to find the radius of a sphere circumscribed about a cube whose edge is given. Let us regard the cube, and the common center of cube and sphere as fixed, but let us vary the radius of the sphere. If this radius is small, the sphere is contained in the cube. As the radius increases, the sphere expands (as a rubber balloon in the process of being inflated). At a certain moment, the sphere touches the faces of the cube; a little later, its edges; still later the sphere passes through the vertices. Which values does the radius assume at these three critical moments?
6. The mathematical experience of the student is incomplete if he never had an opportunity to solve a problem invented by himself. The teacher may show the derivation of new problems from one just solved and, doing so, provoke the curiosity of the students. The teacher may also leave some part of the invention to the students. For instance, he may tell about the expanding sphere we just discussed (under 5) and ask: “What would you try to calculate? Which value of the radius is particularly interesting?”
6. 如果学生没有机会解决自己发明的问题，他的数学经验是不完整的。教师可以展示从刚刚解决的问题中推导出的新问题，这样做可以激起学生的好奇心。教师也可以把发明的某些部分留给学生。例如，他可以讲述我们刚刚讨论过的膨胀球体（第 5 节），并问：“你会尝试计算什么？半径的哪个值特别有意思？”
1. We may use provisional and merely plausible arguments when devising the final and rigorous argument as we use scaffolding to support a bridge during construction. When, however, the work is sufficiently advanced we take off the scaffolding, and the bridge should be able to stand by itself. In the same way, when the solution is sufficiently advanced, we brush aside all kinds of provisional and merely plausible arguments, and the result should be supported by rigorous argument alone.
1. 在设计最终的严格论证时，我们可以使用临时的、仅仅是可信的论证，就像我们在施工过程中使用脚手架来支撑一座桥一样。然而，当工作取得足够的进展时，我们就会取下脚手架，而桥应该能够自己站立起来。同样，当解决方案足够先进时，我们就会把各种临时性的和仅仅是貌似合理的论据放在一边，而结果应该仅仅由严格的论证来支持。
Devising the plan of the solution, we should not be too afraid of merely plausible, heuristic reasoning. Anything is right that leads to the right idea. But we have to change this standpoint when we start carrying out the plan and then we should accept only conclusive, strict arguments. Carrying out your plan of the solution check each step. Can you see clearly that the step is correct?
The more painstakingly we check our steps when carrying out the plan, the more freely we may use heuristic reasoning when devising it.
我们在执行计划时越是煞费苦心地检查我们的步骤，我们在设计计划时就可能越是自由地使用启发式推理。
2. We should give some consideration to the order in which we work out the details of our plan, especially if our problem is complex. We should not omit any detail, we should understand the relation of the detail before us to the whole problem, we should not lose sight of the connection of the major steps. Therefore, we should proceed in proper order.
2. 我们应该考虑一下我们制定计划细节的顺序，特别是在我们的问题很复杂的情况下。我们不应该遗漏任何细节，我们应该了解我们面前的细节与整个问题的关系，我们不应该忽视主要步骤的联系。因此，我们应该按照适当的顺序进行。
In particular, it is not reasonable to check minor details before we have good reasons to believe that the major steps of the argument are sound. If there is a break in the main line of the argument, checking this or that secondary detail would be useless anyhow.
特别是，在我们有充分的理由相信论证的主要步骤是合理的之前，检查次要细节是不合理的。如果论证的主线出现了断裂，检查这个或那个次要的细节无论如何都是无用的。
The order in which we work out the details of the argument may be very different from the order in which we invented them; and the order in which we write down the details in a definitive exposition may be still different. Euclid’s Elements present the details of the argument in a rigid systematic order which was often imitated and often criticized.
我们研究出论证细节的顺序可能与我们发明它们的顺序大不相同；而我们在明确的论述中写下细节的顺序可能仍然不同。欧几里德的《元素》以一种严格的系统化的顺序介绍了论证的细节，这常常被模仿，也常常被批评。
3. In Euclid’s exposition all arguments proceed in the same direction: from the data toward the unknown in “problems to find,” and from the hypothesis toward the conclusion in “problems to prove.” Any new element, point, line, etc., has to be correctly derived from the data or from elements correctly derived in foregoing steps. Any new assertion has to be correctly proved from the hypothesis or from assertions correctly proved in foregoing steps. Each new element, each new assertion is examined when it is encountered first, and so it has to be examined just once; we may concentrate all our attention upon the present step, we need not look behind us, or look ahead. The very last new element whose derivation we have to check, is the unknown. The very last assertion whose proof we have to examine, is the conclusion. If each step is correct, also the last one, the whole argument is correct.
The Euclidean way of exposition can be highly recommended, without reservation, if the purpose is to examine the argument in detail. Especially, if it is our own argument, and it is long and complicated, and we have not only found it but have also surveyed it on large lines so that nothing is left but to examine each particular point in itself, then nothing is better than to write out the whole argument in the Euclidean way.
如果目的是为了详细研究论证，可以毫无保留地大力推荐欧几里得的论述方式。特别是，如果是我们自己的论证，而且它又长又复杂，我们不仅发现了它，而且还对它进行了大范围的调查，以至于除了研究每一个具体的点之外，什么都没有留下，那么没有什么比用欧几里得的方式写出整个论证更好了。
The Euclidean way of exposition, however, cannot be recommended without reservation if the purpose is to convey an argument to a reader or to a listener who never heard of it before. The Euclidean exposition is excellent to show each particular point but not so good to show the main line of the argument. THE INTELLIGENT READER can easily see that each step is correct but has great difficulty in perceiving the source, the purpose, the connection of the whole argument. The reason for this difficulty is that the Euclidean exposition fairly often proceeds in an order exactly opposite to the natural order of invention. (Euclid’s exposition follows rigidly the order of “synthesis”; see PAPPUS, especially comments 3, 4, 5.)
然而，如果目的是向读者或从未听说过的听众传达一个论点，就不能毫无保留地推荐欧氏论述方式。欧几里得的论述方式对于展示每一个特定的观点是非常好的，但对于展示论证的主线却不是那么好。聪明的读者很容易看出每一步都是正确的，但却很难察觉到整个论证的来源、目的和联系。造成这种困难的原因是，欧几里得的论述经常以一种与发明的自然顺序完全相反的顺序进行。（欧几里得的论述严格遵循 “综合” 的顺序；见PAPPUS，特别是评论 3、4、5。）
4. Let us sum up. Euclid’s manner of exposition, progressing relentlessly from the data to the unknown and from the hypothesis to the conclusion, is perfect for checking the argument in detail but far from being perfect for making understandable the main line of the argument.
4. 让我们来总结一下。欧几里德的论述方式，从数据到未知数，从假设到结论的无情推进，对于检查论证的细节是完美的，但对于使人理解论证的主线却远非完美。
It is highly desirable that the students should examine their own arguments in the Euclidean manner, proceeding from the data to the unknown, and checking each step although nothing of this kind should be too rigidly enforced. It is not so desirable that the teacher should present many proofs in the pure Euclidean manner, although the Euclidean presentation may be very useful after a discussion in which, as is recommended by the present book, the students guided by the teacher discover the main idea of the solution as independently as possible. Also desirable seems to be the manner adopted by some textbooks in which an intuitive sketch of the main idea is presented first and the details in the Euclidean order of exposition afterwards.
5. Wishing to satisfy himself that his proposition is true, the conscientious mathematician tries to see it intuitively and to give a formal proof. Can you see clearly that it is correct? Can you prove that it is correct? The conscientious mathematician acts in this respect like the lady who is a conscientious shopper. Wishing to satisfy herself of the quality of a fabric, she wants to see it and to touch it. Intuitive insight and formal proof are two different ways of perceiving the truth, comparable to the perception of a material object through two different senses, sight and touch.
5. 希望让自己确信他的命题是真的，有良知的数学家试图从直觉上看到它，并给出一个正式的证明。你能清楚地看到它是正确的吗？你能证明它是正确的吗？在这方面，有良知的数学家的行为就像一位有良知的购物者。她希望对一块布料的质量感到满意，就想看看它，摸摸它。直觉的洞察力和形式的证明是感知真理的两种不同方式，相当于通过两种不同的感官，即视觉和触觉来感知一个物质对象。
Intuitive insight may rush far ahead of formal proof. Any intelligent student, without any systematic knowledge of solid geometry, can see as soon as he has clearly understood the terms that two straight lines parallel to the same straight line are parallel to each other (the three lines may or may not be in the same plane). Yet the proof of this statement, as given in proposition 9 of the 11th book of Euclid’s Elements, needs a long, careful, and ingenious preparation.
直觉的洞察力可能远远冲在正式证明的前面。任何聪明的学生，在没有任何系统的实体几何知识的情况下，只要他清楚地理解了这些术语，就能看出与同一直线平行的两条直线是相互平行的（这三条线可能在同一平面内，也可能不在同一平面内）。然而，欧几里德《元素》第 11 册命题 9 中对这一说法的证明，需要一个漫长、仔细和巧妙的准备。
Formal manipulation of logical rules and algebraic formulas may get far ahead of intuition. Almost everybody can see at once that 3 straight lines, taken at random, divide the plane into 7 parts (look at the only finite part, the triangle included by the 3 lines). Scarcely anybody is able to see, even straining his attention to the utmost, that 5 planes, taken at random, divide space into 26 parts. Yet it can be rigidly proved that the right number is actually 26, and the proof is not even long or difficult.
Carrying out our plan, we check each step. Checking our step, we may rely on intuitive insight or on formal rules. Sometimes the intuition is ahead, sometimes the formal reasoning. It is an interesting and useful exercise to do it both ways. Can you see clearly that the step is correct? Yes, I can see it clearly and distinctly. Intuition is ahead; but could formal reasoning overtake it? Can you also PROVE that it is correct?
执行我们的计划，我们检查每一个步骤。检查我们的步骤，我们可以依靠直觉的洞察力或正式的规则。有时直觉是领先的，有时则是正式的推理。两种方式都做，是一个有趣而有用的练习。你能清楚地看到这个步骤是正确的吗？是的，我可以清楚地看到它。直觉在前面；但正式推理能不能超越它？你还能 证明 它是正确的吗？
Trying to prove formally what is seen intuitively and to see intuitively what is proved formally is an invigorating mental exercise. Unfortunately, in the classroom there is not always enough time for it. The example, discussed in sections 12 and 14, is typical in this respect.
试图从形式上证明直觉上看到的东西，并从直觉上看到形式上证明的东西，是一种令人振奋的心理锻炼。不幸的是，在课堂上并不总是有足够的时间来做这些。在这方面，第 12 节和第 14 节讨论的例子很典型。
A condition is called redundant if it contains superfluous parts. It is called contradictory if its parts are mutually opposed and inconsistent so that there is no object satisfying the condition.
如果一个条件包含多余的部分，就被称为多余的。如果它的部分是相互对立和不一致的，所以没有满足条件的对象，它就被称为矛盾的。
Thus, if a condition is expressed by more linear equations than there are unknowns, it is either redundant or contradictory; if the condition is expressed by fewer equations than there are unknowns, it is insufficient to determine the unknowns; if the condition is expressed by just as many equations as there are unknowns it is usually just sufficient to determine the unknowns but may be, in exceptional cases, contradictory or insufficient.
Could you derive something useful from the data? We have before us an unsolved problem, an open question. We have to find the connection between the data and the unknown. We may represent our unsolved problem as open space between the data and the unknown, as a gap across which we have to construct a bridge. We can start constructing our bridge from either side, from the unknown or from the data.
Look at the unknown! And try to think of a familiar problem having the same or a similar unknown. This suggests starting the work from the unknown.
看看这个未知数吧!试着去想一个熟悉的问题，有相同或类似的未知数。这表明要从未知的地方开始工作。
Look at the data! Could you derive something useful from the data? This suggests starting the work from the data.
看看这些数据吧!你能从数据中推导出一些有用的东西吗？这表明从数据中开始工作。
It appears that starting the reasoning from the unknown is usually preferable (see PAPPUS and WORKING BACKWARDS). Yet the alternative start, from the data, also has chances of success, must often be tried, and deserves illustration.
看来，从未知数开始推理通常是比较好的（见PAPPUS和WORKING BACKWARDS）。然而，另一种从数据开始的方法也有成功的机会，必须经常尝试，并且值得说明。
Example. We are given three points A, B, and C. Draw a line through A which passes between B and C and is at equal distances from B and C.
例子。给我们三个点A，B，和C。画一条通过A的直线，该直线在B和C之间经过，并且与B和C的距离相等。
What are the data? Three points, A, B, and C, are given in position. We draw a figure, exhibiting the data (Fig. 13).
这些数据是什么？三个点，A、B、C，都有相应的位置。我们画一个图，展示这些数据（图 13）。
What is the condition? The required line passes through A, and passes between B and C, at the same distance from each. We assemble the unknown and the data
条件是什么？所需的线通过A，并在B和C之间通过，与每个人的距离相同。我们把未知数和数据组合起来
FIG. 13
图 13
in a figure exhibiting the required relations (Fig. 14). Our figure, suggested by the definition of the distance of a point from a straight line, shows the right angles involved by this definition.
在一个显示所需关系的图形中（图 14）。我们的图是根据点与直线的距离的定义提出的，显示了这个定义所涉及的直角。
FIG. 14
图 14
The figure, as it is plotted, is still “too empty.” The unknown straight line is still unsatisfactorily connected with the data A, B, and C. The figure needs some auxiliary line, some addition—but what? A fairly good student can get stranded here. There are, of course, various things to try, but the best question to refloat him is: Could you derive something useful from the data?
FIG. 15
图 15
Go back to definitions. See DEFINITION.
返回到定义。见定义。
You examine an object that touches your interest or challenges your curiosity: a house you intend to rent, an important but cryptic telegram, any object whose purpose and origin puzzle you, or any problem you intend to solve. You have an impression of the object as a whole but this impression, possibly, is not definite enough. A detail strikes you, and you focus your attention upon it. Then, you concentrate upon another detail; then, again, upon another. Various combinations of details may present themselves and after a while you again consider the object as a whole but you see it now differently. You decompose the whole into its parts, and you recombine the parts into a more or less different whole.
1. If you go into detail you may lose yourself in details. Too many or too minute particulars are a burden on the mind. They may prevent you from giving sufficient attention to the main point, or even from seeing the main point at all. Think of the man who cannot see the forest for the trees.
1. 如果你深入了解细节，你可能会在细节中迷失自己。太多或太细的细节是心灵的负担。它们可能会妨碍你对主要观点给予足够的关注，甚至根本看不到主要观点。想一想那些不能从树上看到森林的人。
Of course, we do not wish to waste our time with unnecessary detail and we should reserve our effort for the essential. The difficulty is that we cannot say beforehand which details will turn out ultimately as necessary and which will not.
当然，我们不希望在不必要的细节上浪费我们的时间，我们应该把我们的努力保留在必要的地方。困难在于，我们不能事先说哪些细节最终会变成必要的，哪些不会。
Therefore, let us, first of all, understand the problem as a whole. Having understood the problem, we shall be in a better position to judge which particular points may be the most essential. Having examined one or two essential points we shall be in a better position to judge which further details might deserve closer examination. Let us go into detail and decompose the problem gradually, but not further than we need to.
因此，首先，让我们从整体上理解这个问题。在了解了这个问题之后，我们将能够更好地判断哪些具体的要点可能是最重要的。在研究了一两个关键点之后，我们将能更好地判断哪些进一步的细节可能值得更仔细地研究。让我们深入研究细节，逐步分解问题，但不要超过我们需要的范围。
Of course, the teacher cannot expect that all students should act wisely in this respect. On the contrary, it is a very foolish and bad habit with some students to start working at details before having understood the problem as a whole.
当然，老师不能指望所有的学生在这方面都能明智地行事。相反，有些学生在没有理解整个问题之前就开始研究细节，这是一个非常愚蠢的坏习惯。
Having understood the problem as a whole, its aim, its main point, we wish to go into detail. Where should we start? In almost all cases, it is reasonable to begin with the consideration of the principal parts of the problem which are the unknown, the data, and the condition. In almost all cases it is advisable to start the detailed examination of the problem with the questions: What is the unknown? What are the data? What is the condition?
在了解了这个问题的整体情况、其目的、其主要观点之后，我们希望详细了解一下。我们应该从哪里开始呢？几乎在所有情况下，从考虑问题的主要部分开始是合理的，这些部分是未知数、数据和条件。几乎在所有情况下，最好是以问题开始对问题进行详细检查。未知数是什么？数据是什么？条件是什么？
If we wish to examine further details, what should we do? Fairly often, it is advisable to examine each datum by itself, to separate the various parts of the condition, and to examine each part by itself.
如果我们想进一步检查细节，我们应该怎么做？相当多的时候，最好是对每个基准点本身进行检查，把条件的各个部分分开，并对每个部分进行检查。
We may find it necessary, especially if our problem is more difficult, to decompose the problem still further, and to examine still more remote details. Thus, it may be necessary to go back to the definition of a certain term, to introduce new elements involved by the definition, and to examine the elements so introduced.
我们可能会发现有必要，特别是当我们的问题更加困难时，进一步分解问题，并研究更多的细节。因此，可能有必要回到某个术语的定义，引入定义所涉及的新元素，并研究这样引入的元素。
3. After having decomposed the problem, we try to recombine its elements in some new manner. Especially, we may try to recombine the elements of the problem into some new, more accessible problem which we could possibly use as an auxiliary problem.
3. 在对问题进行分解后，我们试图以某种新的方式重新组合其元素。特别是，我们可以尝试将问题的元素重新组合成一些新的、更容易理解的问题，我们可以将其作为一个辅助问题。
There are, of course, unlimited possibilities of recombination. Difficult problems demand hidden, exceptional, original combinations, and the ingenuity of the problem-solver shows itself in the originality of the combination. There are, however, certain usual and relatively simple sorts of combinations, sufficient for simpler problems, which we should know thoroughly and try first, even if we may be obliged eventually to resort to less obvious means.
当然，重组的可能性是无限的。困难的问题需要隐藏的、特殊的、原始的组合，而解决问题的人的聪明才智就表现在组合的原始性上。然而，有一些通常的和相对简单的组合，足以解决较简单的问题，我们应该彻底了解并首先尝试这些组合，即使我们最终可能不得不求助于不太明显的手段。
(1) keep the unknown and change the rest (the data and the condition); or
（1）保留未知数，改变其余部分（数据和条件）；或
(2) keep the data and change the rest (the unknown and the condition); or
（2）保留数据，改变其余部分（未知数和条件）；或
(3) change both the unknown and the data.
（3）同时改变未知数和数据。
We are going to examine these cases.
我们要研究这些案例。
[The cases (1) and (2) overlap. In fact, it is possible to keep both the unknown and the data, and transform the problem by changing the form of the condition alone. For instance, the two following problems, although visibly equivalent, are not exactly the same:
[情况（1）和（2）是重叠的。事实上，可以同时保留未知数和数据，仅通过改变条件的形式来转换问题。例如，下面的两个问题，虽然在视觉上是等价的，但并不完全相同。
Construct an equilateral triangle, being given a side.
构建一个等边三角形，给定一个边。
Construct an equiangular triangle, being given a side.
构建一个等角三角形，给定一个边。
The difference of the two statements which is slight in the present example may be momentous in other cases. Such cases are even important in certain respects but it would take up too much space to discuss them here. Compare AUXILIARY PROBLEMS, 7, last remark.]
在本例中，这两种说法的差异不大，但在其他情况下可能会有重大影响。这种情况在某些方面甚至很重要，但在这里讨论它们会占用太多的空间。比较辅助问题，7，最后一句话] 。
4. Keeping the unknown and changing the data and the condition in order to transform the proposed problem is often useful. The suggestion LOOK AT THE UNKNOWN aims at problems with the same unknown. We may try to recollect a formerly solved problem of this kind: And try to think of a familiar problem having the same or a similar unknown. Failing to remember such a problem we may try to invent one: Could you think of other data appropriate to determine the unknown?
4.保留未知数并改变数据和条件以转化所提出的问题往往是有用的。看未知数 “的建议旨在解决具有相同未知数的问题。我们可以试着回忆一下以前解决过的这类问题。试着去想一个熟悉的问题，有相同或类似的未知数。如果记不起这样的问题，我们可以试着发明一个。你能想到其他合适的数据来确定未知数吗？
A new problem which is more closely related to the proposed problem has a better chance of being useful. Therefore, keeping the unknown, we try to keep also some data and some part of the condition, and to change, as little as feasible, only one or two data and a small part of the condition. A good method is one in which we omit something without adding anything; we keep the unknown, keep only a part of the condition, drop the other part, but do not introduce any new clause or datum. Examples and comments on this case follow under 7, 8.
5. Keeping the data, we may try to introduce some useful and more accessible new unknown. Such an unknown must be obtained from the original data and we have such an unknown in mind when we ask: COULD YOU DERIVE SOMETHING USEFUL FROM THE DATA?
5. 在保留数据的同时，我们可以尝试引入一些有用的、更容易获得的新的未知数。这样的未知数必须从原始数据中获得，当我们问：你能从数据中获得有用的东西吗？
Let us observe that two things are here desirable. First, the new unknown should be more accessible, that is, more easily obtainable from the data than the original unknown. Second, the new unknown should be useful, that is, it should be, when found, capable of rendering some definite service in the search of the original unknown. In short, the new unknown should be a sort of stepping stone. A stone in the middle of the creek is nearer to me than the other bank which I wish to arrive at and, when the stone is reached, it helps me on toward the other bank.
让我们注意到，这里有两件事是可取的。首先，新的未知数应该更容易获得，也就是说，比原来的未知数更容易从数据中获得。第二，新的未知数应该是有用的，也就是说，当它被发现时，应该能够在寻找原始未知数的过程中提供一些明确的服务。简而言之，新的未知数应该是一种踏脚石。小河中间的一块石头比我想到达的另一河岸更靠近我，当我到达这块石头时，它可以帮助我走向另一河岸。
The new unknown should be both accessible and useful but, in practice, we must often content ourselves with less. If nothing better presents itself, it is not unreasonable to derive something from the data that has some chance of being useful; and it is also reasonable to try a new unknown which is closely connected with the original one, even if it does not seem particularly accessible from the outset.
新的未知数应该既容易获得又有用，但在实践中，我们往往必须满足于此。如果没有更好的东西出现，从数据中推导出一些有可能有用的东西也不是没有道理的；尝试一个与原来的未知数密切相关的新未知数也是合理的，即使它从一开始就显得不是特别容易获得。
For instance, if our problem is to find the diagonal of a parallelepiped (as in section 8) we may introduce the diagonal of a face as new unknown. We may do so either because we know that if we have the diagonal of the face we can also obtain the diagonal of the solid (as in section 10); or we may do so because we see that the diagonal of the face is easy to obtain and we suspect that it might be useful in finding the diagonal of the solid. (Compare DID YOU USE ALL THE DATA? 1.)
If our problem is to construct a circle, we have to find two things, its center and its radius; our problem has two parts, we may say. In certain cases, one part is more accessible than the other and therefore, in any case, we may reasonably give a moment’s consideration to this possibility: Could you solve a part of the problem? Asking this, we weigh the chances: Would it pay to concentrate just upon the center, or just upon the radius, and to choose one or the other as our new unknown? Questions of this sort are very often useful. In more complex or in more advanced problems, the decisive idea often consists in carving out some more accessible but essential part from the problem.
如果我们的问题是构造一个圆，我们必须找到两样东西，它的中心和半径；我们的问题有两个部分，我们可以说。在某些情况下，一个部分比另一个部分更容易获得，因此，在任何情况下，我们可以合理地考虑一下这种可能性。你能解决问题的一部分吗？问到这个问题，我们就会权衡机会。是集中精力于中心，还是集中精力于半径，并选择其中之一作为我们的新未知数？这类问题往往很有用。在更复杂或更高级的问题中，决定性的想法往往包括从问题中划出一些更容易获得但又必不可少的部分。
6. Changing both the unknown and the data we deviate more from our original course than in the foregoing cases. This, naturally, we do not like; we sense the danger of losing the original problem altogether. Yet we may be compelled to such an extensive change if less radical changes have failed to produce something accessible and useful, and we may be tempted to recede so far from our original problem if the new problem has a good chance of success. Could you change the unknown, or the data, or both if necessary, so that the new unknown and the new data are nearer to each other?
6. 与前述情况相比，改变未知数和数据，我们会更多地偏离我们原来的方向。这自然是我们不喜欢的；我们感到有可能完全失去原来的问题。然而，如果不那么激进的改变不能产生可获得的和有用的东西，我们可能会被迫进行这样广泛的改变，如果新问题有很好的成功机会，我们可能会受到诱惑而远离我们的原始问题。你能不能改变未知数，或者数据，或者必要时两者都改变，以使新的未知数和新的数据更接近对方？
An interesting way of changing both the unknown and the data is interchanging the unknown with one of the data. (See CAN YOU USE THE RESULT? 3.)
改变未知数和数据的一个有趣方法是将未知数与其中一个数据互换。（参见 “你能使用这个结果吗？”3）。
7. Example. Construct a triangle, being given a side a, the altitude h perpendicular to a, and the angle α opposite to a.
7.例子。构建一个三角形，给定边a，垂直于a的高度h，以及与a相对的角α。
What is the unknown? A triangle.
未知数是什么？一个三角形。
What are the data? Two lines, a and h, and an angle α.
这些数据是什么？两条线，a和h，以及一个角度α。
Now, if we are somewhat familiar with problems of geometric construction, we try to reduce such a problem to the construction of a point. We draw a line BC equal to the given side a; then all that we have to find is the vertex of the triangle A, opposite to a, see Fig. 16. We have, in fact, a new problem.
现在，如果我们对几何结构的问题有点熟悉的话，我们试着把这样的问题简化为点的构造。我们画一条与给定边a相等的线BC；那么我们要找的就是三角形A的顶点，与a相对，见图 16。事实上，我们有一个新的问题。
FIG. 16
图 16
What is the unknown? The point A.
未知数是什么？就是A点。
What are the data? A line h, an angle α, and two points B and C given in position.
这些数据是什么？一条线h，一个角α，以及在位置上给出的两个点B和C。
What is the condition? The perpendicular distance of the point A from the line BC should be h and ∠BAC = α.
该条件是什么？点 A与直线BC的垂直距离应该是h，且∠BAC=α。
In fact, we have transformed our problem, changing both the unknown and the data. The new unknown is a point, the old unknown was a triangle. Some of the data are the same in both problems, the line h and the angle α; but in the old problem we were given a length a and now we are given two points, B and C, instead.
事实上，我们已经改变了我们的问题，改变了未知数和数据。新的未知数是一个点，原来的未知数是一个三角形。两个问题中的一些数据是相同的，如直线h和角度α；但在旧问题中，我们得到了一个长度a，而现在我们得到了两个点，B和C。
The new problem is not difficult. The following suggestion brings us quite near to the solution.
这个新问题并不困难。下面的建议使我们相当接近于解决这个问题。
Separate the various parts of the condition. The condition has two parts, one concerned with the datum h, the other with the datum α. The unknown point is required to be
将条件的各个部分分开。该条件有两部分，一部分与基准点h有关，另一部分与基准点α有关。
(II) the vertex of an angle of given magnitude α, whose sides pass through the given points B and C.
（II）一个给定大小为α的角的顶点，其边通过给定的点B和C。
If we keep only one part of the condition and drop the other part, the unknown point is not completely determined. There are many points satisfying part (I) of the condition, namely all points of a parallel to the line BC at the distance h from BC.2 This parallel is the locus of the points satisfying part (I) of the condition. The locus of the points satisfying part (II) is a certain circular arc whose end-points are B and C. We can describe both loci; their intersection is the point that we desired to construct.
如果我们只保留条件的一部分而放弃另一部分，未知点就不能完全确定。有许多点满足条件的第（I）部分，即与BC的距离为h的直线BC的所有平行点。2这条平行线就是满足条件（I）部分的点的位置。满足条件（二）部分的点的位置是某个圆弧，其端点是B和C。我们可以描述这两个位置；它们的交点是我们想要构建的点。
The procedure that we have just applied has a certain interest; solving problems of geometric construction, we can often follow successfully its pattern: Reduce the problem to the construction of a point, and construct the point as an intersection of two loci.
我们刚刚应用的程序有一定的意义；解决几何构造的问题，我们往往可以成功地遵循其模式。将问题简化为一个点的构造，并将该点构造为两个位置的交点。
But a certain step of this procedure has a still more general interest; solving “problems to find” of any kind, we can follow its pattern: Keep only a part of the condition, drop the other part. Doing so, we weaken the condition of the proposed problem, we restrict less the unknown. How far is the unknown then determined, how can it vary? By asking this, we set, in fact, a new problem. If the unknown is a point in the plane (as it was in our example) the solution of this new problem consists in determining a locus described by the point. If the unknown is a mathematical object of some other kind (it was a square in section 18) we have to describe properly and to characterize precisely a certain set of objects. Even if the unknown is not a mathematical object (as in the next example, under 8) it may be useful to consider, to characterize, to describe, or to list those objects which satisfy a certain part of the condition imposed upon the unknown by the proposed problem.
但这一程序的某个步骤具有更普遍的意义；解决任何类型的 “寻找问题”，我们都可以遵循其模式。只保留条件的一部分，放弃另一部分。这样做，就削弱了所提出的问题的条件，我们对未知数的限制减少了。那么未知数在多大程度上是确定的，它可以如何变化？通过提出这个问题，我们实际上设置了一个新的问题。如果未知数是平面上的一个点（就像我们的例子中那样），这个新问题的解决就包括确定一个由该点描述的位置。如果未知数是其他类型的数学对象（第 18 节中是一个正方形），我们就必须正确地描述并精确地描述一组对象。即使未知数不是一个数学对象（如第 8 节下的下一个例子），考虑、描述、描述或列出那些满足拟议问题对未知数施加的某一部分条件的对象，也可能是有用的。
8. Example. In a crossword puzzle that allows puns and anagrams we find the following clue:
8.例子。在一个允许双关语和变形词的字谜中，我们找到了以下线索。
“Forward and backward part of a machine (5 letters).”
“机器的前进和后退部分（5 个字母）”。
What is the unknown? A word.
未知是什么？一个词。
What is the condition? The word has 5 letters. It has something to do with some part of some machine. It should be, of course, an English word, and not a too unusual one, let us hope.
什么是条件？这个词有 5 个字母。它与某些机器的某些部分有关。当然，它应该是一个英语单词，而且不是一个太特别的单词，让我们希望。
Is the condition sufficient to determine the unknown? No. Or, rather, the condition may be sufficient but that part of the condition which is clear by now is certainly insufficient. There are too many words satisfying it, as “lever,” or “screw,” or what not.
条件是否足以确定未知的东西？不，或者说，条件可能是充分的，但条件中现在已经很清楚的那部分肯定是不充分的。有太多的词可以满足它，如 “杠杆” 或 “螺丝”，或其他什么。
The condition is ambiguously expressed—on purpose, of course. If nothing can be found that could be plausibly described as a “forward part” of a machine and would be a “backward part” too, we may suspect that forward and backward reading might be meant. It may be a good idea to examine this interpretation of the clue.
当然，这个条件的表达是模糊的，是故意的。如果没有任何东西可以被合理地描述为机器的 “前向部分”，并且也是 “后向部分”，我们就会怀疑可能是指前向和后向阅读。研究一下对线索的这种解释可能是一个好主意。
Separate the various parts of the condition. The condition has two parts, one concerned with the meaning of the word, the other with its spelling. The unknown word is required to be
把条件的各个部分分开。该条件有两个部分，一个是关于该词的含义，另一个是关于其拼写。未知的词被要求是
(I) a short word meaning some part of some machine;
（I）一个简短的词，意思是一些机器的某些部分。
(II) a word with 5 letters which spelled backward give again a word meaning some part of some machine.
（II）一个有 5 个字母的单词，倒过来拼写又是一个单词，意思是一些机器的某些部分。
If we keep only one part of the condition and drop the other part, the unknown is not completely determined. There are many words satisfying part (I) of the condition, we have a sort of locus. We may “describe” this locus (I), “follow” it to its “intersection” with locus (II). The natural procedure is to concentrate upon part (I) of the condition, to recollect words having the prescribed meaning and, when we have succeeded in recollecting some such word, to examine whether it has or has not the prescribed length and can or cannot be read backward. We may have to recollect several words before we run into the right one: lever, screw, wheel, shaft, hinge, motor.
Of course, “rotor”!
当然，“转子”!
9. Under 3, we classified the possibilities of obtaining a new “problem to find” by recombining certain elements of a proposed “problem to find.” If we do not introduce just one new problem, but two or more new problems, there are more possibilities which we have to mention but do not attempt to classify.
9. 在 3 下，我们对通过重新组合一个拟议的 “寻找问题” 的某些元素而获得一个新 “寻找问题” 的可能性进行了分类。如果我们不只是引入一个新问题，而是引入两个或更多的新问题，就会有更多的可能性，我们必须提及，但并不试图进行分类。
Still other possibilities may arise. Especially, the solution of a “problem to find” may depend on the solution of a “problem to prove.” We just mention this important possibility; considerations of space prevent us from discussing it.
还可能出现其他的可能性。特别是，一个 “要找的问题” 的解决可能取决于一个 “要证明的问题” 的解决。我们只是提到这种重要的可能性；空间的考虑使我们无法讨论它。
10. Only few and short remarks can be added concerning “problems to prove”; they are analogous to the foregoing more extensive comments on “problems to find” (2 to 9).
10. 关于 “需要证明的问题”，只能补充一些简短的意见；它们类似于前面对 “需要发现的问题”（2 至 9）的广泛评论。
Having understood such a problem as a whole, we should, in general, examine its principal parts. The principal parts are the hypothesis and the conclusion of the theorem that we are required to prove or to disprove. We should understand these parts thoroughly: What is the hypothesis? What is the conclusion? If there is need to get down to more particular points, we may separate the various parts of the hypothesis, and consider each part by itself. Then we may proceed to other details, decomposing the problem further and further.
在了解了这样一个问题的整体之后，一般来说，我们应该研究其主要部分。主要部分是要求我们证明或反驳的假设和定理的结论。我们应该彻底了解这些部分。假设是什么？结论是什么？如果需要深入到更多的细节，我们可以将假设的各个部分分开，并对每个部分进行单独考虑。然后，我们可以进入其他细节，将问题进一步分解，再进一步分解。
(1) We keep the conclusion and change the hypothesis. We first try to recollect such a theorem: Look at the conclusion! And try to think of a familiar theorem having the same or a similar conclusion. If we do not succeed in recollecting such a theorem we try to invent one: Could you think of another hypothesis from which you could easily derive the conclusion? We may change the hypothesis by omitting something without adding anything: Keep only a part of the hypothesis, drop the other part; is the conclusion still valid?
（1）我们保留结论，改变假设。我们首先试着回忆一下这样一个定理。看看这个结论!并试着想出一个熟悉的具有相同或类似结论的定理。如果我们不能成功地回忆起这样一个定理，我们就尝试发明一个。你能想出另一个假设，从这个假设中你可以很容易地推导出结论吗？我们可以通过省略某些东西而不增加任何东西来改变假设：只保留假设的一部分，放弃另一部分；结论是否仍然有效？
(2) We keep the hypothesis and change the conclusion: Could you derive something useful from the hypothesis?
（2）我们保留假设，改变结论。你能从假说中得出一些有用的东西吗？
(3) We change both the hypothesis and the conclusion. We may be more inclined to change both if we have had no success in changing just one. Could you change the hypothesis, or the conclusion, or both if necessary, so that the new hypothesis and the new conclusion are nearer to each other?
（3）我们同时改变假设和结论。如果我们只改变了一个，却没有成功，我们可能更倾向于同时改变这两个。你能不能改变假设，或者结论，或者必要时同时改变，使新的假设和新的结论更接近对方？
We do not attempt to classify here the various possibilities which arise when, in order to solve the proposed “problem to prove,” we introduce two or more new “problems to prove,” or when we link it up with an appropriate “problem to find.”
我们不打算在这里对各种可能性进行分类，这些可能性是：为了解决所提出的 “要证明的问题”，我们引入了两个或更多新的 “要证明的问题”，或者我们把它与一个适当的 “要找到的问题” 联系起来。
1. Technical terms in mathematics are of two kinds. Some are accepted as primitive terms and are not defined. Others are considered as derived terms and are defined in due form; that is, their meaning is stated in primitive terms and in formerly defined derived terms. Thus, we do not give a formal definition of such primitive notions as point, straight line, and plane.3 Yet we give formal definitions of such notions as “bisector of an angle” or “circle” or “parabola.”
1. 数学中的技术术语有两类。有些被认为是原始术语，没有定义。其他术语被认为是派生术语，并以适当的形式加以定义；也就是说，它们的含义是以原始，并以以前定义的派生术语来说明。因此，我们没有对点、直线和平面等原始概念给出正式的定义。3然而，我们给出了 “角的平分线” 或 “圆” 或 “抛物线” 等概念的正式定义。
The definition of the last quoted term may be stated as follows. We call parabola the locus of points which are at equal distance from a fixed point and a fixed straight line. The fixed point is called the focus of the parabola, the fixed line its directrix. It is understood that all elements considered are in a fixed plane, and that the fixed point (the focus) is not on the fixed line (the directrix).
最后引用的术语的定义可以说明如下。我们称抛物线为与一个固定点和一条固定直线距离相等的点的位置。固定点被称为抛物线的焦点，固定直线被称为其直角。可以理解的是，所考虑的所有元素都在一个固定的平面内，并且固定点（焦点）不在固定线（直角）上。
The reader is not supposed to know the meaning of the terms defined: parabola, focus of the parabola, directrix of the parabola. But he is supposed to know the meaning of all the other terms as point, straight line, plane, distance of a point from another point, fixed, locus, etc.
读者不应该知道定义的术语的含义：抛物线、抛物线的焦点、抛物线的直角。但他应该知道所有其他术语的含义，如点、直线、平面、一个点与另一个点的距离、固定、位置等等。
2. Definitions in dictionaries are not very much different from mathematical definitions in the outward form but they are written in a different spirit.
2.词典中的定义与数学定义的外在形式没有太大区别，但它们是以不同的精神书写的。
The writer of a dictionary is concerned with the current meaning of the words. He accepts, of course, the current meaning and states it as neatly as he can in form of a definition.
词典的作者关注的是词语的当前含义。当然，他接受当前的含义，并以定义的形式尽可能整齐地陈述它。
The mathematician is not concerned with the current meaning of his technical terms, at least not primarily concerned with that. What “circle” or “parabola” or other technical terms of this kind may or may not denote in ordinary speech matters little to him. The mathematical definition creates the mathematical meaning.
数学家不关心他的技术术语的当前含义，至少不是主要关心这个。圆 “或” 抛物线 “或其他这类技术术语在普通话中可能表示或不表示什么对他来说并不重要。数学定义创造了数学意义。
Our approach to any problem must depend on the state of our knowledge. Our approach to the present problem depends mainly on the extent of our acquaintance with the properties of the parabola. If we know much about the parabola we try to make use of our knowledge and to extract something helpful from it: Do you know a theorem that could be useful? Do you know a related problem? If we know little about parabola, focus, and directrix, these terms are rather embarrassing and we naturally wish to get rid of them. How can we get rid of them? Let us listen to the dialogue of the teacher and the student discussing the proposed problem. They have chosen already a suitable notation: P for any of the unknown points of intersection, F for the focus, d for the directrix, c for the straight line intersecting the parabola.
我们处理任何问题的方法必须取决于我们的知识状况。我们处理目前问题的方法主要取决于我们对抛物线特性的熟悉程度。如果我们对抛物线有很多了解，我们就会努力利用我们的知识，从中提取一些有用的东西。你知道一个可能有用的定理吗？你知道一个相关的问题吗？如果我们对抛物线、焦点和直角坐标知之甚少，这些术语就相当令人尴尬，我们自然希望摆脱它们。我们怎样才能摆脱它们呢？让我们听听老师和学生在讨论这个问题时的对话。他们已经选择了一个合适的符号。P代表任何一个未知的交点，F代表焦点，d代表直角，c代表与抛物线相交的直线。
“And what is the unknown?”
“那么未知的是什么呢？”
“The point P.”
“点P”。
“What are the data?”
“数据是什么？”
“The straight lines c and d, and the point F.”
“直线c和d，以及点F。”
“What is the condition?”
“条件是什么？”
“P is a point of intersection of the straight line c and of the parabola whose directrix is d and focus F.”
“P是直线c和抛物线的交点，抛物线的直角是d，焦点是F。”
“Correct. You had little opportunity, I know, to study the parabola but you can say, I think, what a parabola is.”
“正确。我知道，你没有什么机会研究抛物线，但你可以说，我想，抛物线是什么。”
“The parabola is the locus of points equidistant from the focus and the directrix.”
“抛物线是与焦点和直角线等距离的点的位置。”
“Correct. You remember the definition correctly. That is right, but we must also use it; go back to definitions. By virtue of the definition of the parabola, what can you say about your point P?”
“正确。你正确地记住了定义。这是对的，但我们也必须使用它；回到定义上。根据抛物线的定义，你能对你的点P说些什么？”
“Good! Draw a figure.”
“好!画个图吧。”
FIG. 17
图 17
The student introduces into Fig. 17 the lines PF and PQ, this latter being the perpendicular to d from P.
学生在图 17中引入直线PF和PQ，后者是从P到d的垂直线。
“Now, could you restate the problem?”
“现在，你能重述一下这个问题吗？”
. . . . .
…… . . .
“Could you restate the condition of the problem, using the lines you have just introduced?”
“你能用你刚才介绍的台词，重述一下问题的条件吗？”
“P is a point on the line c such that PF = PQ.”
“P是直线c上的一个点，使PF=PQ。”
“Good. But please, say it in words: What is PQ?”
“好。但请你用语言说出来。什么是PQ？”
“The perpendicular distance of P from d.”
“P与d的垂直距离”。
“Good. Could you restate the problem now? But please, state it neatly, in a round sentence.”
“很好。你现在能重述这个问题吗？但请你整齐地陈述，用一个圆形的句子。”
“Construct a point P on the given straight line c at equal distances from the given point F and the given straight line d.”
“在给定的直线c上构建一个点P，与给定的点F和给定的直线d距离相等。”
“Observe the progress from the original statement to your restatement. The original statement of the problem was full of unfamiliar technical terms, parabola, focus, directrix; it sounded just a little pompous and inflated. And now, nothing remains of those unfamiliar technical terms; you have deflated the problem. Well done!”
“观察一下从最初的陈述到你重新陈述的进展。问题的原始陈述充满了不熟悉的技术术语，抛物线、焦点、直角仪；它听起来有点浮夸和膨胀。而现在，那些不熟悉的技术术语什么都没有了；你已经把问题放空了。干得好！”
In order to eliminate a technical term we must know its definition; but it is not enough to know the definition, we must use it. In the foregoing example, it was not enough to remember the definition of the parabola. The decisive step was to introduce into the figure the lines PF and PQ whose equality was granted by the definition of the parabola. This is the typical procedure. We introduce suitable elements into the conception of the problem. On the basis of the definition, we establish relations between the elements we introduced. If these relations express completely the meaning, we have used the definition. Having used its definition, we have eliminated the technical term.
为了消除一个技术术语，我们必须知道它的定义；但仅仅知道定义是不够的，我们必须使用它。在前面的例子中，仅仅记住抛物线的定义是不够的。决定性的一步是在图中引入直线PF和PQ，抛物线的定义赋予了它们的平等性。这就是典型的程序。我们在问题的概念中引入适当的元素。在定义的基础上，我们在我们引入的元素之间建立关系。如果这些关系完全表达了意义，我们就使用了这个定义。在使用其定义后，我们就消除了技术术语。
The procedure just described may be called going back to definitions.
刚刚描述的程序可以称为回到定义。
By going back to the definition of a technical term, we get rid of the term but introduce new elements and new relations instead. The resulting change in our conception of the problem may be important. At any rate, some restatement, some VARIATION OF THE PROBLEM is bound to result.
通过回到一个技术术语的定义，我们摆脱了这个术语，而是引入了新的元素和新的关系。在我们对问题的概念中产生的变化可能是重要的。无论如何，一些重述，一些问题的变化是必然会产生的。
5. Definitions and known theorems. If we know the name “parabola” and have some vague idea of the shape of the curve but do not know anything else about it, our knowledge is obviously insufficient to solve the problem proposed as example, or any other serious geometric problem about the parabola. What kind of knowledge is needed for such a purpose?
5.定义和已知定理。如果我们知道 “抛物线” 这个名字，并对曲线的形状有一些模糊的概念，但对它没有任何其他了解，我们的知识显然不足以解决作为例子提出的问题，或任何其他关于抛物线的严重几何问题。这样的目的需要什么样的知识呢？
The science of geometry may be considered as consisting of axioms, definitions, and theorems. The parabola is not mentioned in the axioms which deal only with such primitive terms as point, straight line, and so on. Any geometric argumentation concerned with the parabola, the solution of any problem involving it, must use either its definition or theorems about it. To solve such a problem, we must know, at least, the definition but it is better to know some theorems too.
What we said about the parabola is true, of course, of any derived notion. As we start solving a problem that involves such a notion, we cannot know yet what will be preferable to use, the definition of the notion, or some theorem about it; but it is certain that we have to use one or the other.
我们关于抛物线所说的，当然也适用于任何派生概念。当我们开始解决一个涉及这样一个概念的问题时，我们还不能知道使用什么比较好，是这个概念的定义，还是关于这个概念的一些定理；但可以肯定的是，我们必须使用其中之一。
There are cases, however, in which we have no choice. If we know just the definition of the notion, and nothing else, then we are obliged to use the definition. If we do not know much more than the definition, our best chance may be to go back to the definition. But if we know many theorems about the notion, and have much experience in its use, there is some chance that we may get hold of a suitable theorem involving it.
然而，在有些情况下，我们没有选择。如果我们只知道这个概念的定义，而没有其他东西，那么我们就必须使用这个定义。如果我们知道的不多于定义，我们最好的机会可能是回到定义。但是如果我们知道很多关于这个概念的定理，并且在使用方面有很多经验，那么我们就有可能掌握一个涉及这个概念的合适定理。
6. Several definitions. The sphere is usually defined as the locus of points at a given distance from a given point. (The points are now in space, not restricted to a plane.) Yet the sphere could also be defined as the surface described by a circle revolving about a diameter. Still other definitions of the sphere are known, and many others possible.
6.几个定义。球体通常被定义为与给定点有一定距离的点的位置。（这些点现在是在空间中，而不是限制在一个平面上。）然而，球体也可以定义为一个围绕直径旋转的圆所描述的表面。球体的其他定义也是已知的，还有许多其他可能的定义。
When we have to solve a proposed problem involving some derived notion, as “sphere” or “parabola,” and we wish to go back to its definition, we may have a choice among various definitions. Much may depend in such a case on choosing the definition that fits the case.
当我们必须解决一个涉及某些派生概念的拟议问题时，如 “球体” 或 “抛物线”，而我们希望回到它的定义，我们可能在各种定义中进行选择。在这种情况下，很大程度上取决于选择适合这种情况的定义。
To find the area of the surface of the sphere was, at the time Archimedes solved it, a great and difficult problem. Archimedes had the choice between the definitions of the sphere we just quoted. He preferred to conceive the sphere as the surface generated by a circle revolving about a fixed diameter. He inscribes in the circle a regular polygon, with an even number of sides, of which the fixed diameter joins opposite vertices. The regular polygon approximates the circle and, revolving with the circle, generates a convex surface composed of two cones with vertices at the extremities of the fixed diameter and of several frustums of cones in between. This composite surface approximates the sphere and is used by Archimedes in computing the area of the surface of the sphere. If we conceive the sphere as the locus of points equally distant from the center, no such simple approximation to its surface is suggested.
7. Going back to definitions is important in inventing an argument but it is also important in checking it.
7. 回到定义在发明论证中很重要，但在检查论证中也很重要。
Somebody presents an alleged new solution of Archimedes’ problem of finding the area of the surface of the sphere. If he has only a vague idea of the sphere, his solution will not be any good. He may have a clear idea of the sphere but if he fails to use this idea in his argument I cannot know that he had any idea at all, and his argument is no good. Therefore, listening to the argument, I am waiting for the moment when he is going to say something substantial about the sphere, to use its definition or some theorem about it. If such a moment never comes, the solution is no good.
有人提出了一个所谓的阿基米德寻找球体表面面积问题的新解决方案。如果他对球体只有一个模糊的概念，他的解决方案就不会有任何好处。他可能对球体有一个清晰的概念，但如果他在论证中没有使用这个概念，我就不能知道他有任何概念，他的论证也就没有意义。因此，听着他的论证，我在等待他说一些关于球体的实质性内容，使用它的定义或一些关于它的定理。如果这样的时刻永远不会到来，那么这个解决方案就不好了。
We should check not only the arguments of others but, of course, also our own arguments, in the same way. Have you taken into account all essential notions involved in the problem? How did you use this notion? Did you use its meaning, its definition? Did you use essential facts, known theorems about it?
我们不仅要检查别人的论点，当然也要检查自己的论点，以同样的方式。你是否考虑到了问题中涉及的所有基本概念？你是如何使用这个概念的？你是否使用了它的含义，它的定义？你是否使用了关于它的基本事实、已知定理？
That going back to definitions is important in examining the validity of an argument was emphasized by Pascal who stated the rule: “Substituer mentalement les définitions à la place des définis.” The meaning is: “Substitute mentally the defining facts for the defined terms.” That going back to definitions is also important in devising an argument was emphasized by Hadamard.
8. Going back to definitions is an important operation of the mind. If we wish to understand why the definitions of words are so important, we should realize first that words are important. We can hardly use our mind without using words, or signs, or symbols of some sort. Thus, words and signs have power. Primitive peoples believe that words and symbols have magic power. We may understand such belief but we should not share it. We should know that the power of a word does not reside in its sound, in the “vocis flatus,” in the “hot air” produced by the speaker, but in the ideas of which the word reminds us and, ultimately, in the facts on which the ideas are based.
8. 回到定义上是一种重要的思维操作。如果我们想了解为什么词语的定义如此重要，我们首先应该认识到，词语是重要的。如果不使用文字，或符号，或某种象征，我们几乎无法使用我们的思想。因此，词语和符号具有力量。原始人相信，文字和符号具有神奇的力量。我们可以理解这种信念，但我们不应该分享它。我们应该知道，一个词的力量不在于它的声音，不在于 “vocis flatus”，不在于说话者产生的 “热空气”，而在于这个词让我们想起的思想，最终在于这些思想所依据的事实。
Therefore, it is a sound tendency to seek meaning and facts behind the words. Going back to definitions, the mathematician seeks to get hold of the actual relations of mathematical objects behind the technical terms, as the physicist seeks definite experiments behind his technical terms, and the common man with some common sense wants to get down to hard facts and not to be fooled by mere words.
因此，寻求词语背后的意义和事实是一种健全的倾向。回到定义上，数学家寻求掌握技术术语背后的数学对象的实际关系，正如物理学家在他的技术术语背后寻求明确的实验一样，而具有一定常识的普通人则希望踏踏实实地了解铁的事实，不被单纯的文字所迷惑。
Descartes, René (1596-1650), great mathematician and philosopher, planned to give a universal method to solve problems but he left unfinished his Rules for the Direction of the Mind. The fragments of this treatise, found in his manuscripts and printed after his death, contain more—and more interesting—materials concerning the solution of problems than his better known work Discours de la Méthode although the “Discours” was very likely written after the “Rules.” The following lines of Descartes seem to describe the origin of the “Rules”: “As a young man, when I heard about ingenious inventions, I tried to invent them by myself, even without reading the author. In doing so, I perceived, by degrees, that I was making use of certain rules.”
Determination, hope, success. It would be a mistake to think that solving problems is a purely “intellectual affair”; determination and emotions play an important role. Lukewarm determination and sleepy consent to do a little something may be enough for a routine problem in the classroom. But, to solve a serious scientific problem, will power is needed that can outlast years of toil and bitter disappointments.
1. Determination fluctuates with hope and hopelessness, with satisfaction and disappointment. It is easy to keep on going when we think that the solution is just around the corner; but it is hard to persevere when we do not see any way out of the difficulty. We are elated when our forecast comes true. We are depressed when the way we have followed with some confidence is suddenly blocked, and our determination wavers.
1. 决心随着希望和无望，随着满意和失望而波动。当我们认为解决方案就在眼前时，我们很容易坚持下去；但当我们看不到任何摆脱困难的方法时，就很难坚持下去。当我们的预测成真时，我们会感到欣喜。当我们满怀信心走过的路突然受阻，而我们的决心也随之动摇时，我们就会感到沮丧。
“Il n’est point besoin espérer pour entreprendre ni réussir pour persévérer.” “You can undertake without hope and persevere without success.” Thus may speak an inflexible will, or honor and duty, or a nobleman with a noble cause. This sort of determination, however, would not do for the scientist, who should have some hope to start with, and some success to go on. In scientific work, it is necessary to apportion wisely determination to outlook. You do not take up a problem, unless it has some interest; you settle down to work seriously if the problem seems instructive; you throw in your whole personality if there is a great promise. If your purpose is set, you stick to it, but you do not make it unnecessarily difficult for yourself. You do not despise little successes, on the contrary, you seek them: If you cannot solve the proposed problem try to solve first some related problem.
“Il n'est point besoin espérer pour entreprendre ni réussir pour persévérer。”“你可以不抱希望地进行，不成功地坚持下去。” 这样可以说是一种不灵活的意志，或荣誉和责任，或有崇高事业的贵族。然而，这种决心对科学家来说是不可行的，他应该有一些希望来开始，有一些成功来继续。在科学工作中，有必要将决心明智地分配给前景。除非你对一个问题有兴趣，否则你不会接受这个问题；如果这个问题看起来很有启发性，你就会安下心来认真工作；如果有很大的希望，你就会投入你的整个。如果你的目标已经确定，你就会坚持下去，但你不会给自己带来不必要的困难。你不会轻视小的成功，相反，你会寻求它们。如果你不能解决所提出的问题，你会尝试先解决一些相关的问题。
2. When a student makes really silly blunders or is exasperatingly slow, the trouble is almost always the same; he has no desire at all to solve the problem, even no desire to understand it properly, and so he has not understood it. Therefore, a teacher wishing seriously to help the student should, first of all, stir up his curiosity, give him some desire to solve the problem. The teacher should also allow some time to the student to make up his mind, to settle down to his task.
2. 当一个学生犯了非常愚蠢的错误或令人气愤的迟钝时，麻烦几乎总是一样的；他根本没有解决这个问题的欲望，甚至没有正确理解这个问题的欲望，所以他没有理解它。因此，一个希望认真帮助学生的老师，首先应该激起他的好奇心，让他有一些解决问题的欲望。老师也应该给学生一些时间，让他下定决心，安下心来完成他的任务。
Teaching to solve problems is education of the will. Solving problems which are not too easy for him, the student learns to persevere through unsuccess, to appreciate small advances, to wait for the essential idea, to concentrate with all his might when it appears. If the student had no opportunity in school to familiarize himself with the varying emotions of the struggle for the solution his mathematical education failed in the most vital point.
解决问题的教学是意志的教育。解决那些对他来说不太容易的问题，学生要学会在失败中坚持，欣赏微小的进步，等待重要的想法，在它出现时全力以赴。如果学生在学校里没有机会熟悉为解决问题而斗争的各种情绪，那么他的数学教育在最关键的一点上就失败了。
Diagnosis is used here as a technical term in education meaning “closer characterization of the student’s work.” A grade characterizes the student’s work but somewhat crudely. The teacher, wishing to improve the student’s work, needs a closer characterization of good and bad points as the physician, wishing to improve the patient’s health, needs a diagnosis.
Incomplete understanding of the problem, owing to lack of concentration, is perhaps the most widespread deficiency in solving problems. With respect to devising a plan and obtaining a general idea of the solution two opposite faults are frequent. Some students rush into calculations and constructions without any plan or general idea; others wait clumsily for some idea to come and cannot do anything that would accelerate its coming. In carrying out the plan, the most frequent fault is carelessness, lack of patience in checking each step. Failure to check the result at all is very frequent; the student is glad to get an answer, throws down his pencil, and is not shocked by the most unlikely results.
由于注意力不集中，对问题的理解不全面，可能是解决问题中最普遍的缺陷。在制定计划和获得解决方案的总体思路方面，经常出现两种相反的错误。一些学生在没有任何计划或总体想法的情况下就匆匆忙忙地进行计算和建造；另一些学生则笨拙地等待着一些想法的出现，但却不能做任何事情来加速想法的出现。在执行计划时，最常见的错误是粗心大意，缺乏耐心检查每一个步骤。完全不检查结果是非常常见的；学生很高兴得到一个答案，扔下铅笔，并不为最不可能的结果所震惊。
The teacher, having made a careful diagnosis of a fault of this kind, has some chance to cure it by insisting on certain questions of the list.
教师在对这种错误进行仔细诊断后，有一定的机会通过坚持做清单中的某些问题来治愈它。
Did you use all the data? Owing to the progressive mobilization of our knowledge, there will be much more in our conception of the problem at the end than was in it at the outset (PROGRESS AND ACHIEVEMENT, 1). But how is it now? Have we got what we need? Is our conception adequate? Did you use all the data? Did you use the whole condition? The corresponding question concerning “problems to prove” is: Did you use the whole hypothesis?
1. For an illustration, let us go back to the “parallelepiped problem” stated in section 8 (and followed up in sections 10, 12, 14, 15). It may happen that a student runs into the idea of calculating the diagonal of a face,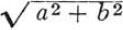 
, but then he gets stuck. The teacher may help him by asking: Did you use all the data? The student can scarcely fail to observe that the expression 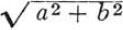does not contain the third datum c. Therefore, he should try to bring c into play. Thus, he has a good chance to observe the decisive right triangle whose legs are 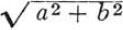and c, and whose hypotenuse is the desired diagonal of the parallelepiped. (For another illustration see AUXILIARY ELEMENTS, 3.)
The questions we discuss here are very important. Their use in constructing the solution is clearly shown by the foregoing example. They may help us to find the weak spot in our conception of the problem. They may point out a missing element. When we know that a certain element is still missing, we naturally try to bring it into play. Thus, we have a clue, we have a definite line of inquiry to follow, and have a good chance to meet with the decisive idea.
我们在这里讨论的问题是非常重要的。它们在构建解决方案中的用途在前面的例子中已经清楚地表明了。它们可以帮助我们找到我们对问题的概念中的薄弱点。它们可能会指出一个缺失的元素。当我们知道某个元素仍然缺失时，我们自然会试图让它发挥作用。这样，我们就有了一条线索，有了一条明确的调查路线可循，并有很大的机会接触到决定性的想法。
2. The questions we discussed are helpful not only in constructing an argument but also in checking it. In order to be more concrete, let us assume that we have to check the proof of a theorem whose hypothesis consists of three parts, all three essential to the truth of the theorem. That is, if we discard any part of the hypothesis, the theorem ceases to be true. Therefore, if the proof neglects to use any part of the hypothesis, the proof must be wrong. Does the proof use the whole hypothesis? Does it use the first part of the hypothesis? Where does it use the first part of the hypothesis? Where does it use the second part? Where the third? Answering to all these questions we check the proof.
2. 我们讨论的问题不仅对构建论证有帮助，而且对检查论证也有帮助。为了更加具体，让我们假设我们必须检查一个定理的证明，该定理的假设由三部分组成，这三部分对于定理的真实性都是至关重要的。也就是说，如果我们放弃了假设的任何部分，该定理就不再是真的。因此，如果证明忽略了使用假说的任何部分，那么证明一定是错误的。该证明是否使用了整个假说？它是否使用了假说的第一部分？它在哪里使用了假设的第一部分？在哪里使用了第二部分？第三部分在哪里？回答了所有这些问题，我们就可以检查证明了。
This sort of checking is effective, instructive, and almost necessary for thorough understanding if the argument is long and heavy—as THE INTELLIGENT READER should know.
这种检查是有效的、有启发性的，而且如果论点很长、很重，几乎是彻底理解的必要条件 —— 正如《聪明的读者》应该知道的。
3. The questions we discussed aim at examining the completeness of our conception of the problem. Our conception is certainly incomplete if we fail to take into account any essential datum or condition or hypothesis. But it is also incomplete if we fail to realize the meaning of some essential term. Therefore, in order to examine our conception, we should also ask: Have you taken into account all essential notions involved in the problem? See DEFINITION, 7.
4. The foregoing remarks, however, are subject to caution and certain limitations. In fact, their straightforward application is restricted to problems which are “perfectly stated” and “reasonable.”
4. 然而，上述意见需要谨慎对待并受到某些限制。事实上，它们的直接应用仅限于那些 “完美陈述” 和 “合理” 的问题。
A perfectly stated and reasonable “problem to find” must have all necessary data and not a single superfluous datum; also its condition must be just sufficient, neither contradictory nor redundant. In solving such a problem, we have to use, of course, all the data and the whole condition.
一个完美的陈述和合理的 “要找的问题” 必须有所有必要的数据，没有一个多余的数据；它的条件也必须是恰到好处的，既不矛盾也不多余。在解决这样一个问题时，我们当然要使用所有的数据和整个条件。
The object of a “problem to prove” is a mathematical theorem. If the problem is perfectly stated and reasonable, each clause in the hypothesis of the theorem must be essential to the conclusion. In proving such a theorem we have to use, of course, each clause of the hypothesis.
一个 “待证问题” 的对象是一个数学定理。如果这个问题被完美地表述出来并且是合理的，那么该定理的假设中的每一个条款都必须是结论的关键。在证明这样一个定理时，我们当然要使用假设中的每一个条款。
Mathematical problems proposed in traditional textbooks are supposed to be perfectly stated and reasonable. We should however not rely too much on this; when there is the slightest doubt, we should ask: IS IT POSSIBLE TO SATISFY THE CONDITION? Trying to answer this question, or a similar one, we may convince ourselves, at least to a certain extent, that our problem is as good as it is supposed to be.
传统教科书中提出的数学问题应该是完美的、合理的。然而，我们不应过分依赖这一点；当有丝毫疑问时，我们应该问：是否有可能满足条件？试图回答这个问题或类似的问题，我们可能会说服自己，至少在某种程度上，我们的问题和它被认为的一样好。
The question stated in the title of the present article and allied questions may and should be asked without modification only when we know that the problem before us is reasonable and perfectly stated or when, at least, we have no reason to suspect the contrary.
只有当我们知道摆在我们面前的问题是合理的、完美的，或者至少我们没有理由怀疑是相反的时候，才可以而且应该不加修改地提出本文标题中所述的问题以及相关问题。
PRACTICAL PROBLEMS however are usually far from being perfectly stated and require a thorough reconsideration of the questions discussed in the present article.
然而，实际问题通常远远没有得到完美的说明，需要对本文讨论的问题进行彻底的重新考虑。
Do you know a related problem? We can scarcely imagine a problem absolutely new, unlike and unrelated to any formerly solved problem; but, if such a problem could exist, it would be insoluble. In fact, when solving a problem, we always profit from previously solved problems, using their result, or their method, or the experience we acquired solving them. And, of course, the problems from which we profit must be in some way related to our present problem. Hence the question: Do you know a related problem?
There is usually no difficulty at all in recalling formerly solved problems which are more or less related to our present one. On the contrary, we may find too many such problems and there may be difficulty in choosing a useful one. We have to look around for closely related problems; we LOOK AT THE UNKNOWN, or we look for a formerly solved problem which is linked to our present one by GENERALIZATION, SPECIALIZATION, or ANALOGY.
回忆以前解决的问题通常没有什么困难，这些问题或多或少与我们现在的问题有关。相反，我们可能会发现太多这样的问题，而且选择一个有用的问题可能会有困难。我们必须四处寻找密切相关的问题；我们寻找未知的问题，或者我们寻找以前解决的问题，这些问题与我们现在的问题通过通用化、专门化或类似化联系起来。
The question we discuss here aims at the mobilization of our formerly acquired knowledge (PROGRESS AND ACHIEVEMENT, 1). An essential part of our mathematical knowledge is stored in the form of formerly proved theorems. Hence the question: Do you know a theorem that could be useful? This question may be particularly suitable when our problem is a “problem to prove,” that is, when we have to prove or disprove a proposed theorem.
我们在这里讨论的问题旨在调动我们以前获得的知识（《进步与成就》，1）。我们数学知识的一个重要部分是以以前证明的定理的形式储存的。因此，有这样一个问题。你知道一个可能有用的定理吗？当我们的问题是一个 “证明问题” 时，也就是说，当我们必须证明或反驳一个拟议的定理时，这个问题可能特别合适。
Examine your guess. Your guess may be right, but it is foolish to accept a vivid guess as a proven truth—as primitive people often do. Your guess may be wrong. But it is also foolish to disregard a vivid guess altogether—as pedantic people sometimes do. Guesses of a certain kind deserve to be examined and taken seriously: those which occur to us after we have attentively considered and really understood a problem in which we are genuinely interested. Such guesses usually contain at least a fragment of the truth although, of course, they very seldom show the whole truth. Yet there is a chance to extract the whole truth if we examine such a guess appropriately.
Many a guess has turned out to be wrong but nevertheless useful in leading to a better one.
许多猜测都被证明是错误的，但还是有助于引导更好的猜测。
No idea is really bad, unless we are uncritical. What is really bad is to have no idea at all.
没有什么想法是真正糟糕的，除非我们是不加批判的。真正糟糕的是根本没有想法。
1. Don’t. Here is a typical story about Mr. John Jones. Mr. Jones works in an office. He had hoped for a little raise but his hope, as hopes often are, was disappointed. The salaries of some of his colleagues were raised but not his. Mr. Jones could not take it calmly. He worried and worried and finally suspected that Director Brown was responsible for his failure in getting a raise.
1.不要。这里有一个关于约翰·琼斯先生的典型故事。琼斯先生在一个办公室工作。他曾希望能得到一点加薪，但他的希望，就像希望经常发生的那样，却落空了。他的一些同事的工资被提高了，但他的却没有。琼斯先生无法平静地接受这个事实。他忧心忡忡，最后怀疑布朗主任对他未能加薪负有责任。
We cannot blame Mr. Jones for having conceived such a suspicion. There were indeed some signs pointing to Director Brown. The real mistake was that, after having conceived that suspicion, Mr. Jones became blind to all signs pointing in the opposite direction. He worried himself into firmly believing that Director Brown was his personal enemy and behaved so stupidly that he almost succeeded in making a real enemy of the director.
我们不能责怪琼斯先生怀有这样的怀疑。确实有一些迹象指向布朗主任。真正的错误在于，在产生了这种怀疑之后，琼斯先生对所有指向相反方向的迹象视而不见。他忧心忡忡，坚信布朗主任是他的个人敌人，并表现得如此愚蠢，以至于他几乎成功地与该主任成为真正的敌人。
The trouble with Mr. John Jones is that he behaves like most of us. He never changes his major opinions. He changes his minor opinions not infrequently and quite suddenly; but he never doubts any of his opinions, major or minor, as long as he has them. He never doubts them, or questions them, or examines them critically—he would especially hate critical examination, if he understood what that meant.
Let us concede that Mr. John Jones is right to a certain extent. He is a busy man; he has his duties at the office and at home. He has little time for doubt or examination. At best, he could examine only a few of his convictions and why should he doubt one if he has no time to examine that doubt?
让我们承认，约翰·琼斯先生在某种程度上是对的。他是个大忙人；他在办公室和家里都有自己的职责。他没有什么时间去怀疑或审查。充其量，他只能审查他的几个信念，如果他没有时间审查这种怀疑，他为什么要怀疑一个信念？
Still, don’t do as Mr. John Jones does. Don’t let your suspicion, or guess, or conjecture, grow without examination till it becomes ineradicable. At any rate, in theoretical matters, the best of ideas is hurt by uncritical acceptance and thrives on critical examination.
但是，不要像约翰·琼斯先生那样做。不要让你的怀疑，或猜测，或猜想，不经审查而增长，直到它成为不可动摇。无论如何，在理论问题上，最好的想法会因不加批判地接受而受到伤害，而在批判性的审查中茁壮成长。
2. A mathematical example. Of all quadrilaterals with given perimeter, find the one that has the greatest area.
2.一个数学上的例子。在所有具有给定周长的四边形中，找出面积最大的一个。
What is the unknown? A quadrilateral.
未知数是什么？一个四边形。
What are the data? The perimeter of the quadrilateral is given.
这些数据是什么？四边形的周长已经给出。
What is the condition? The required quadrilateral should have a greater area than any other quadrilateral with the same perimeter.
条件是什么？所要求的四边形的面积应该大于周长相同的任何其他四边形。
This problem is very different from the usual problems in elementary geometry and, therefore, it is quite natural to start guessing.
这个问题与初级几何中的通常问题非常不同，因此，开始猜测是很自然的。
Which quadrilateral is likely to be the one with the greatest area? What would be the simplest guess? We may have heard that of all figures with the same perimeter the circle has the greatest area; we may even suspect some reason for the plausibility of this statement. Now, which quadrilateral comes nearest to the circle? Which one comes nearest to it in symmetry?
哪个四边形可能是面积最大的那个？最简单的猜测是什么？我们可能听说过，在所有周长相同的图形中，圆的面积最大；我们甚至可能怀疑这种说法的合理性。现在，哪个四边形离圆最近？哪一个在对称性上与它最接近？
The square is a pretty obvious guess. If we take this guess seriously, we should realize what it means. We should have the courage to state it: “Of all quadrilaterals with given perimeter the square has the greatest area.” If we decide ourselves to examine this statement, the situation changes. Originally, we had a “problem to find.” After having formulated our guess, we have a “problem to prove”; we have to prove or disprove the theorem formulated.
If we do not know any problem similar to ours that has been solved before, we may find our task pretty tough. If you cannot solve the proposed problem, try to solve first some related problem. Could you solve a part of the problem? It may occur to us that if the square is privileged among quadrilaterals it must, by that very fact, also be privileged among rectangles. A part of our problem would be solved if we could succeed in proving the following statement: “Of all rectangles with given perimeter the square has the greatest area.”
如果我们不知道任何与我们类似的问题，而且以前也被解决过，我们可能会发现我们的任务相当艰难。如果你不能解决所提出的问题，可以先试着解决一些相关的问题。你能解决问题的一部分吗？我们可能会想到，如果正方形在四边形中享有特权，那么根据这一事实，它在长方形中也享有特权。如果我们能够成功地证明下面的陈述，我们的问题的一部分就会得到解决。“在所有具有一定周长的长方形中，正方形的面积最大。”
This theorem appears more accessible than the former; it is, of course, weaker. At any rate, we should realize what it means; we should have the courage to restate it in more detail. We can restate it advantageously in the language of algebra.
这个定理似乎比前者更容易理解；当然，它更弱。无论如何，我们应该意识到它的含义；我们应该有勇气更详细地重述它。我们可以用代数的语言有利地重述它。
The area of a rectangle with adjacent sides a and b is ab. Its perimeter is 2a + 2b.
一个相邻边为a和b的长方形的面积是ab。它的周长是2a+2b。
One side of the square that has the same perimeter as the rectangle just mentioned is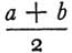 
. Thus, the area of this square is 
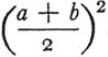. It should be greater than the area of the rectangle, and so we should have
正方形的一条边与刚才提到的长方形的周长相同，是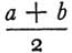 。因此，这个正方形的面积是 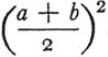。它应该大于长方形的面积，所以我们应该有
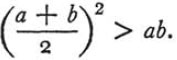
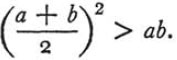
This, however, is true, for it is equivalent to
然而，这是真的，因为它相当于
or to
或向
and this inequality certainly holds, unless a = b, that is, the rectangle examined is a square.
而这个不等式当然成立，除非a=b，也就是说，被检查的矩形是一个正方形。
We have not solved our problem yet, but we have made some progress just by facing squarely our rather obvious guesses.
我们还没有解决我们的问题，但仅仅通过正视我们相当明显的猜测，我们已经取得了一些进展。
3. A nonmathematical example. In a certain crossword puzzle we have to find a word with seven letters, and the clue is: “Do the walls again, back and forth.”4
3.一个非数学的例子。在某个填字游戏中，我们必须找到一个有 7 个字母的单词，线索是。“再做一次墙，来回做”。4
What is the unknown? A word.
未知是什么？一个词。
What are the data? The length of the word is given; it has seven letters.
这些数据是什么？给出了这个词的长度，它有七个字母。
What is the condition? It is stated in the clue. It has something to do with walls, yet it is still very hazy.
条件是什么？线索中提到了。它与墙壁有关，但仍然很模糊。
Thus, we have to reexamine the clue. As we do so, the last part may catch our attention: “. . . again, back and forth.” Could you solve a part of the problem? Here is a chance to guess the beginning of the word. Since the repetition is so strongly emphasized, the word, quite possibly, might start with “re.” This is a pretty obvious guess. If we are tempted to believe it, we should realize what it means. The word required would look thus:
因此，我们必须重新审视这条线索。当我们这样做时，最后一部分可能会引起我们的注意。“…… 再一次，来来回回。”你能解决一部分的问题吗？这里是一个猜测该词开头的机会。由于重复被如此强烈地强调，这个词很可能以 “re” 开头。这是一个相当明显的猜测。如果我们很想相信它，我们应该意识到它的含义。所需的词会这样看。
Can you check the result? If another word of the puzzle crosses the one just considered in the first letter, we have an R to start that other word. It may be a good idea to switch to that other word and check the R. If we succeed in verifying that R or if, at least, we do not find any reason against it, we come back to our original word. We ask again: What is the condition? As we reexamine the clue, the very last part may catch our attention: “. . . back and forth.” Could this imply that the word we seek can be read not only forward but backward? This is a less obvious guess (yet there are such cases, see DECOMPOSING AND RECOMBINING, 8).
At any rate, let us face this guess; let us realize what it means. The word would look as follows:
无论如何，让我们面对这个猜测；让我们意识到它的含义。这个词会看起来如下。
Moreover, the third letter should be the same as the fifth; it is very likely a consonant and the fourth or middle letter a vowel.
此外，第三个字母应与第五个字母相同；它很可能是一个辅音，第四个或中间的字母是元音。
The reader can now easily guess the word by himself. If nothing else helps, he can try all the vowels, one after the other, for the letter in the middle.
现在，读者可以很容易地自己猜出这个词。如果没有其他的帮助，他可以尝试所有的元音，一个接一个地去找中间的字母。
1. If our problem is a problem of geometry, we have to consider a figure. This figure may be in our imagination, or it may be traced on paper. On certain occasions, it might be desirable to imagine the figure without drawing it; but if we have to examine various details, one detail after the other, it is desirable to draw a figure. If there are many details, we cannot imagine all of them simultaneously, but they are all together on the paper. A detail pictured in our imagination may be forgotten; but the detail traced on paper remains, and, when we come back to it, it reminds us of our previous remarks, it saves us some of the trouble we have in recollecting our previous consideration.
2. We now consider more specially the use of figures in problems of geometric construction.
2. 我们现在更特别地考虑数字在几何结构问题中的使用。
We start the detailed consideration of such a problem by drawing a figure containing the unknown and the data, all these elements being assembled as it is prescribed by the condition of the problem. In order to understand the problem distinctly, we have to consider each datum and each part of the condition separately; then we reunite all parts and consider the condition as a whole, trying to see simultaneously the various connections required by the problem. We would scarcely be able to handle and separate and recombine all these details without a figure on paper.
我们开始详细考虑这样一个问题，先画一个包含未知数和数据的图，所有这些元素都按照问题的条件规定进行组合。为了清楚地理解这个问题，我们必须分别考虑每个数据和条件的每个部分；然后我们把所有部分重新组合起来，把条件作为一个整体来考虑，试图同时看到问题所要求的各种联系。如果没有纸上的图表，我们几乎不可能处理、分离和重新组合所有这些细节。
On the other hand, before we have solved the problem definitively, it remains doubtful whether such a figure can be drawn at all. Is it possible to satisfy the whole condition imposed by the problem? We are not entitled to say Yes before we have obtained the definitive solution; nevertheless we begin with assuming a figure in which the unknown is connected with the data as prescribed by the condition. It seems that, drawing the figure, we have made an unwarranted assumption.
另一方面，在我们明确地解决这个问题之前，是否能画出这样一个数字仍然是个疑问。是否有可能满足这个问题提出的全部条件？在我们得到确定的解决方案之前，我们无权说 “是”；然而，我们从假设一个图形开始，其中的未知数与条件规定的数据相联系。看来，在画这个图时，我们做了一个毫无根据的假设。
No, we have not. Not necessarily. We do not act incorrectly when, examining our problem, we consider the possibility that there is an object that satisfies the condition imposed upon the unknown and has, with all the data, the required relations, provided we do not confuse mere possibility with certainty. A judge does not act incorrectly when, questioning the defendant, he considers the hypothesis that the defendant perpetrated the crime in question, provided he does not commit himself to this hypothesis. Both the mathematician and the judge may examine a possibility without prejudice, postponing their judgment till the examination yields some definite result.
The method of starting the examination of a problem of construction by drawing a sketch on which, supposedly, the condition is satisfied, goes back to the Greek geometers. It is hinted by the short, somewhat enigmatic phrase of Pappus: Assume what is required to be done as already done. The following recommendation is somewhat less terse but clearer: Draw a hypothetical figure which supposes the condition of the problem satisfied in all its parts.
通过画一张草图来开始研究一个建筑问题的方法可以追溯到希腊的几何学家，据说条件已经满足。帕普斯的一句简短而有点神秘的话语暗示了这一点。假设需要做的事情已经做了。下面的建议不那么简明，但更清晰。画一个假设的图形，假设问题的条件在所有部分都得到满足。
This is a recommendation for problems of geometric construction but in fact there is no need to restrict us to any such particular kind of problem. We may extend the recommendation to all “problems to find” stating it in the following general form: Examine the hypothetical situation in which the condition of the problem is supposed to be fully satisfied.
这是对几何构造问题的建议，但实际上没有必要将我们限制在任何这种特定的问题上。我们可以把这个建议扩展到所有的 “要找的问题”，用以下的一般形式来说明它。检查假设的情况，在这种情况下，问题的条件被认为是完全满足的。
Compare PAPPUS, 6.
比较PAPPUS，6。
3. Let us discuss a few points about the actual drawing of figures.
3. 让我们来讨论一下关于实际画图的几点意见。
(I) Shall we draw the figures exactly or approximately, with instruments or free-hand?
（I）我们应该准确地或近似地、用工具或自由地画出数字吗？
Both kinds of figures have their advantages. Exact figures have, in principle, the same role in geometry as exact measurements in physics; but, in practice, exact figures are less important than exact measurements because the theorems of geometry are much more extensively verified than the laws of physics. The beginner, however, should construct many figures as exactly as he can in order to acquire a good experimental basis; and exact figures may suggest geometric theorems also to the more advanced. Yet, for the purpose of reasoning, carefully drawn free-hand figures are usually good enough, and they are much more quickly done. Of course, the figure should not look absurd; lines supposed to be straight should not be wavy, and so-called circles should not look like potatoes.
An inaccurate figure can occasionally suggest a false conclusion, but the danger is not great and we can protect ourselves from it by various means, especially by varying the figure. There is no danger if we concentrate upon the logical connections and realize that the figure is a help, but by no means the basis of our conclusions; the logical connections constitute the real basis. [This point is instructively illustrated by certain well known paradoxes which exploit cleverly the intentional inaccuracy of the figure.]
一个不准确的数字偶尔会暗示一个错误的结论，但危险性不大，我们可以通过各种手段保护自己，特别是通过改变数字。如果我们把注意力集中在逻辑联系上，并认识到数字是一种帮助，但绝不是我们结论的基础；逻辑联系才是真正的基础，就不会有危险。[某些众所周知的悖论巧妙地利用了数字的故意不准确，从而很好地说明了这一点。］
(II) It is important that the elements are assembled in the required relations, it is unimportant in which order they are constructed. Therefore, choose the most convenient order. For example, to illustrate the idea of trisection, you wish to draw two angles, α and β, so that α = 3β. Starting from an arbitrary α, you cannot construct β with ruler and compasses. Therefore, you choose a fairly small, but otherwise arbitrary β and, starting from β, you construct α which is easy.
（二）重要的是各元素按要求的关系组合起来，以何种顺序构建并不重要。因此，请选择最方便的顺序。例如，为了说明三分法的概念，你希望画两个角，α和β，使α=3β。从一个任意的α开始，你不能用尺子和圆规构建β。因此，你选择一个相当小的，但在其他方面是任意的β，从β开始，你构建α，这很容易。
(III) Your figure should not suggest any undue specialization. The different parts of the figure should not exhibit apparent relations not required by the problem. Lines should not seem to be equal, or to be perpendicular, when they are not necessarily so. Triangles should not seem to be isosceles, or right-angled, when no such property is required by the problem. The triangle having the angles 45°, 60°, 75° is the one which, in a precise sense of the word, is the most “remote” both from the isosceles, and from the right-angled shape.5 You draw this, or a not very different triangle, if you wish to consider a “general” triangle.
（III）你的图表不应暗示任何不适当的专业化。图中的不同部分不应表现出问题所不要求的明显关系。线条不应该看起来是相等的，或者是垂直的，但它们不一定是这样。三角形不应该看起来是等腰三角形或直角形，而问题并不要求这种性质。具有 45°、60°、75°角的三角形，从准确的意义上说，是与等腰三角形和直角形最 “遥远” 的一个。5如果你想考虑一个 “一般” 的三角形，你可以把它画在，或者一个不太一样的三角形。
(IV) In order to emphasize the different roles of different lines, you may use heavy and light lines, continuous and dotted lines, or lines in different colors. You draw a line very lightly if you are not yet quite decided to use it as an auxiliary line. You may draw the given elements with red pencil, and use other colors to emphasize important parts, as a pair of similar triangles, etc.
（四）为了强调不同线条的不同作用，你可以使用重线和轻线，连续线和虚线，或者不同颜色的线条。如果你还没有完全决定把一条线作为辅助线，你就把它画得很轻。你可以用红色铅笔画出给定的元素，用其他颜色来强调重要部分，如一对相似的三角形等。
(V) In order to illustrate solid geometry, shall we use three-dimensional models, or drawings on paper and blackboard?
（五）为了说明实体几何，我们应该使用三维模型，还是在纸和黑板上画图？
Three-dimensional models are desirable, but troublesome to make and expensive to buy. Thus, usually, we must be satisfied with drawings although it is not easy to make them impressive. Some experimentation with self-made cardboard models is very desirable for beginners. It is helpful to take objects of our everyday surroundings as representations of geometric notions. Thus, a box, a tile, or the classroom may represent a rectangular parallelepiped, a pencil, a circular cylinder, a lampshade, the frustum of a right circular cone, etc.
三维模型是可取的，但制作起来很麻烦，购买起来也很昂贵。因此，通常情况下，我们必须对图纸感到满意，尽管要使它们令人印象深刻并不容易。对于初学者来说，用自制的纸板模型进行一些实验是非常可取的。把我们日常生活中的物体作为几何概念的代表是有帮助的。因此，一个盒子、一块瓦片或教室可以代表一个长方形的平行四边形、一支铅笔、一个圆筒、一个灯罩、一个直角圆锥体的外壳，等等。
4. Figures traced on paper are easy to produce, easy to recognize, easy to remember. Plane figures are especially familiar to us, problems about plane figures especially accessible. We may take advantage of this circumstance, we may use our aptitude for handling figures in handling nongeometrical objects if we contrive to find a suitable geometrical representation for those nongeometrical objects.
4. 在纸上描画的图形容易产生，容易识别，容易记忆。平面图形对我们来说特别熟悉，关于平面图形的问题特别容易获得。我们可以利用这种情况，我们可以利用我们处理图形的能力来处理非几何物体，如果我们设法为这些非几何物体找到一个合适的几何表示。
In fact, geometrical representations, graphs and diagrams of all sorts, are used in all sciences, not only in physics, chemistry, and the natural sciences, but also in economics, and even in psychology. Using some suitable geometrical representation, we try to express everything in the language of figures, to reduce all sorts of problems to problems of geometry.
Thus, even if your problem is not a problem of geometry, you may try to draw a figure. To find a lucid geometric representation for your nongeometrical problem could be an important step toward the solution.
因此，即使你的问题不是一个几何学问题，你也可以尝试画一个图形。为你的非几何学问题找到一个清晰的几何学表现，可能是走向解决的重要一步。
1. If, by some chance, we come across the sum
1. 如果在某些情况下，我们遇到了和
we may observe that it can be expressed in the curious form
我们可以看到，它可以用奇怪的形式来表达
Now, it is natural to ask ourselves: Does it often happen that a sum of successive cubes as
现在，我们自然要问自己。是否经常发生这样的情况：一个连续的立方体的总和为
is a square? In asking this, we generalize. This generalization is a lucky one; it leads from one observation to a remarkable general law. Many results were found by lucky generalizations in mathematics, physics, and the natural sciences. See INDUCTION AND MATHEMATICAL INDUCTION.
是一个正方形？在问这个问题时，我们进行了概括。这种归纳是一种幸运的归纳；它从一个观察结果引出一个显著的一般规律。在数学、物理学和自然科学中，许多结果都是通过幸运的归纳发现的。请参阅归纳法和数学归纳法。
2. Generalization may be useful in the solution of problems. Consider the following problem of solid geometry: “A straight line and a regular octahedron are given in position. Find a plane that passes through the given line and bisects the volume of the given octahedron.” This problem may look difficult but, in fact, very little familiarity with the shape of the regular octahedron is sufficient to suggest the following more general problem: “A straight line and a solid with a center of symmetry are given in position. Find a plane that passes through the given line and bisects the volume of the given solid.” The plane required passes, of course, through the center of symmetry of the solid, and is determined by this point and the given line. As the octahedron has a center of symmetry, our original problem is also solved.
The reader will not fail to observe that the second problem is more general than the first, and, nevertheless, much easier than the first. In fact, our main achievement in solving the first problem was to invent the second problem. Inventing the second problem, we recognize the role of the center of symmetry; we disentangled that property of the octahedron which is essential for the problem at hand, namely that it has such a center.
读者不会不注意到，第二个问题比第一个问题更普遍，但也比第一个问题容易得多。事实上，我们解决第一个问题的主要成就是发明了第二个问题。在发明第二个问题时，我们认识到了对称中心的作用；我们分解了八面体的那个属性，这个属性对当前的问题至关重要，即它有这样一个中心。
The more general problem may be easier to solve. This sounds paradoxical but, after the foregoing example, it should not be paradoxical to us. The main achievement in solving the special problem was to invent the general problem. After the main achievement, only a minor part of the work remains. Thus, in our case, the solution of the general problem is only a minor part of the solution of the special problem.
更普遍的问题可能更容易解决。这听起来很矛盾，但在前面的例子之后，它对我们来说不应该是矛盾的。解决特殊问题的主要成就是发明一般问题。在主要的成就之后，只剩下小部分的工作。因此，在我们的案例中，一般问题的解决只是特殊问题解决的一个小部分。
See INVENTOR’S PARADOX.
见 “发明家范例”。
3. “Find the volume of the frustum of a pyramid with square base, being given that the side of the lower base is 10 in., the side of the upper base 5 in., and the altitude of the frustum 6 in.” If for the numbers 10, 5, 6 we substitute letters, for instance a, b, h, we generalize. We obtain a more general problem than the original one, namely the following: “Find the volume of the frustum of a pyramid with square base, being given that the side of the lower base is a, the side of the upper base b, and the altitude of the frustum h.” Such generalization may be very useful. Passing from a problem “in numbers” to another one “in letters” we gain access to new procedures; we can vary the data, and, doing so, we may check our results in various ways. See CAN YOU CHECK THE RESULT? 2, VARIATION OF THE PROBLEM, 4.
Have you seen it before? It is possible that we have solved before the same problem that we have to do now, or that we have heard of it, or that we had a very similar problem. These are possibilities which we should not fail to explore. We try to remember what happened. Have you seen it before? Or have you seen the same problem in a slightly different form? Even if the answer is negative such questions may start the mobilization of useful knowledge.
The question in the title of the present article is often used in a more general meaning. In order to obtain the solution, we have to extract relevant elements from our memory, we have to mobilize the pertinent parts of our dormant knowledge (PROGRESS AND ACHIEVEMENT). We cannot know, of course, in advance which parts of our knowledge may be relevant; but there are certain possibilities which we should not fail to explore. Thus, any feature of the present problem that played a role in the solution of some other problem may play again a role. Therefore, if any feature of the present problem strikes us as possibly important, we try to recognize it. What is it? Is it familiar to you? Have you seen it before?
本文标题中的问题常常被用在一个更普遍的意义上。为了获得解决方案，我们必须从我们的记忆中提取相关的元素，我们必须调动我们沉睡的知识中的相关部分（《进步与成就》）。当然，我们不能事先知道我们的知识中哪些部分可能是相关的；但有一些可能性，我们不应该不去探索。因此，目前问题的任何特征，如果在其他问题的解决中发挥了作用，就可能再次发挥作用。因此，如果目前问题的任何特征让我们觉得可能很重要，我们就会试着去认识它。它是什么？你对它熟悉吗？你以前见过它吗？
Here is a problem related to yours and solved before. This is good news; a problem for which the solution is known and which is connected with our present problem, is certainly welcome. It is still more welcome if the connection is close and the solution simple. There is a good chance that such a problem will be useful in solving our present one.
The situation that we are discussing here is typical and important. In order to see it clearly let us compare it with the situation in which we find ourselves when we are working at an auxiliary problem. In both cases, our aim is to solve a certain problem A and we introduce and consider another problem B in the hope that we may derive some profit for the solution of the proposed problem A from the consideration of that other problem B. The difference is in our relation to B. Here, we succeeded in recollecting an old problem B of which we know the solution but we do not know yet how to use it. There, we succeeded in inventing a new problem B; we know (or at least we suspect strongly) how to use B, but we do not know yet how to solve it. Our difficulty concerning B makes all the difference between the two situations. When this difficulty is overcome, we may use B in the same way in both cases; we may use the result or the method (as explained in AUXILIARY PROBLEM, 3), and, if we are lucky, we may use both the result and the method. In the situation considered here, we know well the solution of B but we do not know yet how to use it. Therefore, we ask: Could you use it? Could you use its result? Could you use its method?
我们在这里讨论的情况是典型而重要的。为了清楚地看到它，让我们把它与我们在处理一个辅助问题时发现自己所处的情况进行比较。在这两种情况下，我们的目标都是解决某个问题A，我们引入并考虑另一个问题B，希望我们能从对另一个问题B的考虑中获得解决所提议的问题A的一些好处。在这里，我们成功地发明了一个新的问题B；我们知道（或至少我们强烈怀疑）如何使用B，但我们还不知道如何解决它。我们关于B的困难使这两种情况完全不同。当这个困难被克服后，我们可以在两种情况下以同样的方式使用B；我们可以使用结果或方法（如辅助问题3 中所解释的），如果我们幸运的话，我们可以同时使用结果和方法。在这里考虑的情况下，我们清楚地知道B的解，但我们还不知道如何使用它。因此，我们问：你能使用它吗？你能使用它的结果吗？你能使用它的方法吗？
The intention of using a certain formerly solved problem influences our conception of the present problem. Trying to link up the two problems, the new and the old, we introduce into the new problem elements corresponding to certain important elements of the old problem. For example, our problem is to determine the sphere circumscribed about a given tetrahedron. This is a problem of solid geometry. We may remember that we have solved before the analogous problem of plane geometry of constructing the circle circumscribed about a given triangle. Then we recollect that in the old problem of plane geometry, we used the perpendicular bisectors of the sides of the triangle. It is reasonable to try to introduce something analogous into our present problem. Thus we may be led to introduce into our present problem, as corresponding auxiliary elements, the perpendicular bisecting planes of the edges of the tetrahedron. After this idea, we can easily work out the solution to the problem of solid geometry, following the analogous solution in plane geometry.
The foregoing example is typical. The consideration of a formerly solved related problem leads us to the introduction of auxiliary elements, and the introduction of suitable auxiliary elements makes it possible for us to use the related problem to full advantage in solving our present problem. We aim at such an effect when, thinking about the possible use of a formerly solved related problem, we ask: Should you introduce some auxiliary element in order to make its use possible?
前面的例子很典型。对以前解决的相关问题的考虑导致我们引入辅助元素，而引入合适的辅助元素使我们有可能在解决我们现在的问题时充分使用相关问题。当我们考虑到以前解决的相关问题的可能用途时，我们会问：你是否应该引入一些辅助元素，以使其使用成为可能？
Here is a theorem related to yours and proved before. This version of the remark discussed here is exemplified in section 19.
这里有一个与你相关的定理，并在之前被证明。这里讨论的这一版本的评论在第 19 节中有例证。
Heuristic, or heuretic, or “ars inveniendi” was the name of a certain branch of study, not very clearly circumscribed, belonging to logic, or to philosophy, or to psychology, often outlined, seldom presented in detail, and as good as forgotten today. The aim of heuristic is to study the methods and rules of discovery and invention. A few traces of such study may be found in the commentators of Euclid; a passage of PAPPUS is particularly interesting in this respect. The most famous attempts to build up a system of heuristic are due to DESCARTES and to LEIBNITZ, both great mathematicians and philosophers. Bernard BOLZANO presented a notable detailed account of heuristic. The present booklet is an attempt to revive heuristic in a modern and modest form. See MODERN HEURISTIC.
Heuristic, as an adjective, means “serving to discover.”
启发式，作为一个形容词，意味着 “为发现服务”。
Heuristic reasoning is reasoning not regarded as final and strict but as provisional and plausible only, whose purpose is to discover the solution of the present problem. We are often obliged to use heuristic reasoning. We shall attain complete certainty when we shall have obtained the complete solution, but before obtaining certainty we must often be satisfied with a more or less plausible guess. We may need the provisional before we attain the final. We need heuristic reasoning when we construct a strict proof as we need scaffolding when we erect a building.
See SIGNS OF PROGRESS. Heuristic reasoning is often based on induction, or on analogy; see INDUCTION AND MATHEMATICAL INDUCTION, and ANALOGY, 8, 9, 10.6
见《进步的标志》。启发式推理通常基于归纳法或类比法；见归纳法和数学归纳法，以及类比法，8、9、10。6
Heuristic reasoning is good in itself. What is bad is to mix up heuristic reasoning with rigorous proof. What is worse is to sell heuristic reasoning for rigorous proof.
启发式推理本身是好的。坏的是把启发式推理和严格的证明混为一谈。更糟的是把启发式推理当作严格的证明来卖。
The teaching of certain subjects, especially the teaching of calculus to engineers and physicists, could be essentially improved if the nature of heuristic reasoning were better understood, both its advantages and its limitations openly recognized, and if the textbooks would present heuristic arguments openly. A heuristic argument presented with taste and frankness may be useful; it may prepare for the rigorous argument of which it usually contains certain germs. But a heuristic argument is likely to be harmful if it is presented ambiguously with visible hesitation between shame and pretension. See WHY PROOFS?
If you cannot solve the proposed problem do not let this failure afflict you too much but try to find consolation with some easier success, try to solve first some related problem; then you may find courage to attack your original problem again. Do not forget that human superiority consists in going around an obstacle that cannot be overcome directly, in devising some suitable auxiliary problem when the original one appears insoluble.
Could you imagine a more accessible related problem? You should now invent a related problem, not merely remember one; I hope that you have tried already the question: Do you know a related problem?
你能想象一个更容易理解的相关问题吗？你现在应该发明一个相关的问题，而不仅仅是记住一个问题；我希望你已经尝试过这个问题了。你知道一个相关的问题吗？
The remaining questions in that paragraph of the list which starts with the title of the present article have a common aim, the VARIATION OF THE PROBLEM. There are different means to attain this aim as GENERALIZATION, SPECIALIZATION, ANALOGY, and others which are various ways of DECOMPOSING AND RECOMBINING.
以本文标题开始的那段列表中的其余问题有一个共同的目标，即问题的变化。实现这一目标有不同的手段，如通用化、专门化、相似化，以及其他各种解构和重组的方式。
Induction and mathematical induction. Induction is the process of discovering general laws by the observation and combination of particular instances. It is used in all sciences, even in mathematics. Mathematical induction is used in mathematics alone to prove theorems of a certain kind. It is rather unfortunate that the names are connected because there is very little logical connection between the two processes. There is, however, some practical connection; we often use both methods together. We are going to illustrate both methods by the same example.
1. We may observe, by chance, that
1. 我们可以观察到，在偶然的情况下，
How does such a thing happen? Does it often happen that such a sum of successive cubes is a square?
这样的事情是如何发生的？这样的连续立方体之和是否经常发生，是一个正方形？
In asking this we are like the naturalist who, impressed by a curious plant or a curious geological formation, conceives a general question. Our general question is concerned with the sum of successive cubes
在提出这个问题时，我们就像自然学家一样，被一种奇特的植物或一种奇特的地质构造所打动，构思出一个一般性的问题。我们的一般问题是关于连续的立方体的总和
We were led to it by the “particular instance” n = 4.
我们是由 “特定实例”n= 4 引导的。
What can we do for our question? What the naturalist would do; we can investigate other special cases. The special cases n = 2, 3 are still simpler, the case n = 5 is the next one. Let us add, for the sake of uniformity and completeness, the case n = 1. Arranging neatly all these cases, as a geologist would arrange his specimens of a certain ore, we obtain the following table:
对于我们的问题，我们能做什么？自然学家会做什么；我们可以调查其他特殊情况。n=2、3 的特殊情况仍然比较简单，n=5 的情况是下一个。为了统一和完整起见，让我们加上n=1 的情况。把所有这些情况整齐地排列起来，就像地质学家排列某种矿石的标本一样，我们得到以下表格。
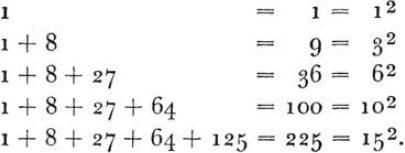
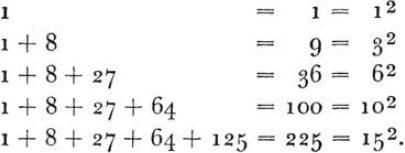
It is hard to believe that all these sums of consecutive cubes are squares by mere chance. In a similar case, the naturalist would have little doubt that the general law suggested by the special cases heretofore observed is correct; the general law is almost proved by induction. The mathematician expresses himself with more reserve although fundamentally, of course, he thinks in the same fashion. He would say that the following theorem is strongly suggested by induction:
很难相信所有这些连续立方体的总和都是方块，仅仅是偶然。在类似的情况下，自然学家几乎不会怀疑由先前观察到的特殊情况所提出的一般规律是正确的；一般规律几乎是由归纳法证明的。数学家的表达方式更为谨慎，尽管从根本上说，他当然是以同样的方式思考问题。他说，以下定理是由归纳法强烈建议的。
What would the naturalist do in such a situation? He would go on examining his conjecture. In so doing, he may follow various lines of investigation. The naturalist may accumulate further experimental evidence; if we wish to do the same, we have to test the next cases, n = 6, 7, . . . . The naturalist may also reexamine the facts whose observation has led him to his conjecture; he compares them carefully, he tries to disentangle some deeper regularity, some further analogy. Let us follow this line of investigation.
在这种情况下，博物学家会怎么做？他将继续研究他的猜想。在这样做的时候，他可以遵循各种调查路线。自然学家可以积累更多的实验证据；如果我们也想这样做，我们必须检验接下来的情况，n=6，7，…… 自然学家也可以重新审查那些观察结果导致他产生猜想的事实；他仔细比较这些事实，试图解开一些更深层次的规律性，一些进一步的类比。让我们沿着这条路线进行调查。
Let us reexamine the cases n = 1, 2, 3, 4, 5 which we arranged in our table. Why are all these sums squares? What can we say about these squares? Their bases are 1, 3, 6, 10, 15. What about these bases? Is there some deeper regularity, some further analogy? At any rate, they do not seem to increase too irregularly. How do they increase? The difference between two successive terms of this sequence is itself increasing,
让我们重新审视我们在表中安排的n=1、2、3、4、5 的情况。为什么这些和都是正方形？我们可以对这些正方形说些什么？它们的基数是 1、3、6、10、15。这些基数是怎么回事？是否有一些更深的规律性，一些进一步的类比？不管怎么说，它们似乎并没有不规则地增加。它们是如何增加的呢？这个序列的两个连续项之间的差值本身就是增加的。
Now these differences are conspicuously regular. We may see here a surprising analogy between the bases of those squares, we may see a remarkable regularity in the numbers 1, 3, 6, 10, 15:
现在，这些差异是显而易见的规律。在这里，我们可以看到这些方格的基数之间有一个惊人的类比，我们可以看到 1、3、6、10、15 这些数字的显著规律性。
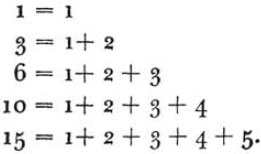
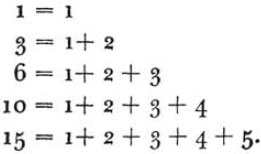
It is, for n = 1, 2, 3, . . .
就是说，对于n=1，2，3，……
3. The law we just stated was found by induction, and the manner in which it was found conveys to us an idea about induction which is necessarily one-sided and imperfect but not distorted. Induction tries to find regularity and coherence behind the observations. Its most conspicuous instruments are generalization, specialization, analogy. Tentative generalization starts from an effort to understand the observed facts; it is based on analogy, and tested by further special cases.
3. 我们刚才所说的规律是通过归纳法发现的，它的发现方式向我们传达了一种关于归纳法的想法，这种想法必然是片面的、不完善的，但不是扭曲的。归纳法试图找到观察结果背后的规律性和连贯性。它最明显的工具是概括化、专门化和类比。暂时性的概括是从理解观察到的事实的努力开始的；它以类比为基础，并通过进一步的特殊情况来检验。
We refrain from further remarks on the subject of induction about which there is wide disagreement among philosophers. But it should be added that many mathematical results were found by induction first and proved later. Mathematics presented with rigor is a systematic deductive science but mathematics in the making is an experimental inductive science.
我们不对归纳法的问题作进一步的评论，因为哲学家们对这个问题存在着广泛的分歧。但应该补充的是，许多数学结果是先通过归纳法发现的，后来才被证明。以严谨的态度提出的数学是一门系统的演绎科学，但正在形成的数学是一门实验性的归纳科学。
4. In mathematics as in the physical sciences we may use observation and induction to discover general laws. But there is a difference. In the physical sciences, there is no higher authority than observation and induction but in mathematics there is such an authority: rigorous proof.
4. 在数学中，如同在物理科学中，我们可以利用观察和归纳来发现一般规律。但有一点不同。在物理科学中，没有比观察和归纳更高的权威，但在数学中，有这样一个权威：严格的证明。
After having worked a while experimentally it may be good to change our point of view. Let us be strict. We have discovered an interesting result but the reasoning that led to it was merely plausible, experimental, provisional, heuristic; let us try to establish it definitively by a rigorous proof.
在实验性地工作了一段时间后，改变我们的观点可能是好的。让我们严格对待。我们已经发现了一个有趣的结果，但导致它的推理仅仅是可信的、实验的、临时的、启发式的；让我们尝试通过严格的证明来确定它。
There is a minor simplification. We may know that
有一个小小的简化。我们可能知道
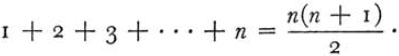
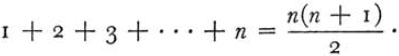
At any rate, this is easy to verify. Take a rectangle with sides n and n + 1, and divide it in two halves by a zigzag line as in Fig. 15a which shows the case n = 4. Each of the halves is “staircase-shaped” and its area has the expression 1 + 2 + · · · + n; for n = 4 it is 1 + 2 + 3 + 4, see Fig. 18b. Now, the whole area of the rectangle is n(n + 1) of which the staircase-shaped area is one half; this proves the formula.
FIG. 18
图 18
We may transform the result which we found by induction into
我们可以将我们通过归纳发现的结果转化为
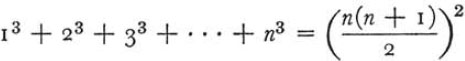
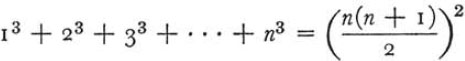
5. If we have no idea how to prove this result, we may at least test it. Let us test the first case we have not tested yet, the case n = 6. For this value, the formula yields
5. 如果我们不知道如何证明这个结果，我们至少可以测试它。让我们测试一下我们还没有测试的第一种情况，即n=6 的情况。对于这个值，公式得出的结果是
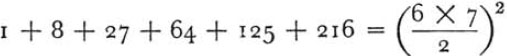
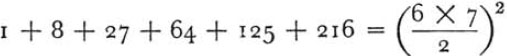
We can test the formula more effectively. The formula is, very likely, generally true, true for all values of n. Does it remain true when we pass from any value n to the next value n + 1? Along with the formula as written above (p. 118) we should also have
我们可以更有效地测试这个公式。这个公式很有可能，一般来说是真的，对n的所有值都是真的。当我们从任何数值n到下一个数值n+1 时，它是否仍然是真的？除了上面写的公式（第 118 页）之外，我们还应该有
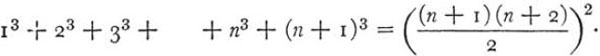
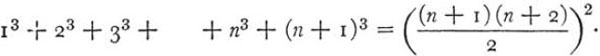
Now, there is a simple check. Subtracting from this the formula written above, we obtain
现在，有一个简单的检查。从这里减去上面写的公式，我们得到
This is, however, easy to check. The right hand side may be written as
然而，这很容易检查。右手边可以写成
Our experimentally found formula passed a vital test.
我们在实验中发现的配方通过了一项重要测试。
Let us see clearly what this test means. We verified beyond doubt that
让我们清楚地看到这个测试的含义。我们毫无疑问地验证了
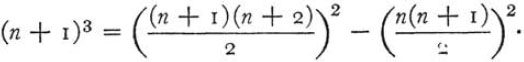
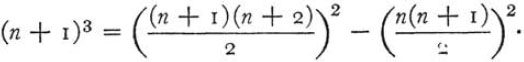
We do not know yet whether
我们还不知道是否
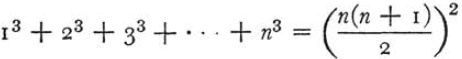
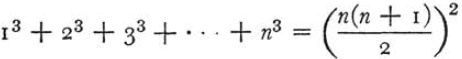
is true. But if we knew that this was true we could infer, by adding the equation which we verified beyond doubt, that
是真的。但是，如果我们知道这是真的，我们就可以通过添加我们验证无疑的方程式来推断，即
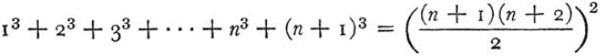
is also true which is the same assertion for the next integer n + 1. Now, we actually know that our conjecture is true for n = 1, 2, 3, 4, 5, 6. By virtue of what we have just said, the conjecture, being true for n = 6, must also be true for n = 7; being true for n = 7 it is true for n = 8; being true for n = 8 it is true for n = 9; and so on. It holds for all n, it is proved to be true generally.
6. The foregoing proof may serve as a pattern in many similar cases. What are the essential lines of this pattern?
6. 上述证明可以作为许多类似案件的模式。这个模式的基本路线是什么？
The assertion we have to prove must be given in advance, in precise form.
我们要证明的论断必须事先以精确的形式给出。
The assertion must depend on an integer n.
该断言必须取决于一个整数n。
The assertion must be sufficiently “explicit” so that we have some possibility of testing whether it remains true in the passage from n to the next integer n + 1.
这个断言必须足够 “明确”，以便我们有某种可能性来测试它在从n到下一个整数n+1 的过程中是否仍然是真的。
If we succeed in testing this effectively, we may be able to use our experience, gained in the process of testing, to conclude that the assertion must be true for n + 1 provided it is true for n. When we are so far it is sufficient to know that the assertion is true for n = 1; hence it follows for n = 2; hence it follows for n = 3. and so on; passing from any integer to the next, we prove the assertion generally.
如果我们成功地进行了有效的测试，我们也许能够利用我们在测试过程中获得的经验，得出结论：只要对n来说是真的，该断言对 n+1 来说就一定是真的。当我们走到这一步时，只需知道该断言对n=1 是真的；因此对n=2 是真的；因此对n=3 是真的，以此类推；从任何一个整数到下一个整数，我们一般地证明该断言。
This process is so often used that it deserves a name. We could call it “proof from n to n + 1” or still simpler “passage to the next integer.” Unfortunately, the accepted technical term is “mathematical induction.” This name results from a random circumstance. The precise assertion that we have to prove may come from any source, and it is immaterial from the logical viewpoint what the source is. Now, in many cases, as in the case we discussed here in detail, the source is induction, the assertion is found experimentally, and so the proof appears as a mathematical complement to induction; this explains the name.
这个过程是如此频繁地使用，以至于它应该有一个名字。我们可以称它为 “从n到n+1 的证明”，或者更简单的 “到下一个整数的通道”。不幸的是，公认的技术术语是 “数学归纳法”。这个名字是由一个随机情况造成的。我们要证明的确切论断可能来自任何来源，从逻辑学的角度来看，来源是什么并不重要。现在，在许多情况下，就像我们在这里详细讨论的案例一样，来源是归纳法，断言是通过实验发现的，因此证明是作为归纳法的数学补充出现的；这解释了这个名字。
7. Here is another point, somewhat subtle, but important to anybody who desires to find proofs by himself. In the foregoing, we found two different assertions by observation and induction, one after the other, the first under 1, the second under 2; the second was more precise than the first. Dealing with the second assertion, we found a possibility of checking the passage from n to n + 1, and so we were able to find a proof by “mathematical induction.” Dealing with the first assertion, and ignoring the precision added to it by the second one, we should scarcely have been able to find such a proof. In fact, the first assertion is less precise, less “explicit,” less “tangible,” less accessible to testing and checking than the second one. Passing from the first to the second, from the less precise to the more precise statement, was an important preparative for the final proof.
This circumstance has a paradoxical aspect. The second assertion is stronger; it implies immediately the first, whereas the somewhat “hazy” first assertion can hardly imply the more “clear-cut” second one. Thus, the stronger theorem is easier to master than the weaker one; this is the INVENTOR’S PARADOX.
这种情况有一个自相矛盾的方面。第二个断言更有力；它立即意味着第一个断言，而有点 “朦胧” 的第一个断言却很难意味着更 “清晰” 的第二个断言。因此，较强的定理比较弱的定理更容易掌握；这就是发明家的悖论。
This sounds paradoxical. Yet, when passing from one problem to another, we may often observe that the new, more ambitious problem is easier to handle than the original problem. More questions may be easier to answer than just one question. The more comprehensive theorem may be easier to prove, the more general problem may be easier to solve.
这听起来很矛盾。然而，当从一个问题转到另一个问题时，我们可能经常观察到，新的、更宏大的问题比原来的问题更容易处理。更多的问题可能比只有一个问题更容易回答。更全面的定理可能更容易证明，更普遍的问题可能更容易解决。
These questions are often useful at an early stage when they do not need a final answer but just a provisional answer, a guess. For examples, see sections 8, 18.
这些问题在早期阶段往往是有用的，因为它们不需要最终的答案，而只是一个临时的答案，一个猜测。例子见第 8、18 节。
It is good to foresee any feature of the result for which we work. When we have some idea of what we can expect, we know better in which direction we should go. Now, an important feature of a problem is the number of solutions of which it admits. Most interesting among problems are those which admit of just one solution; we are inclined to consider problems with a uniquely determined solution as the only “reasonable” problems. Is our problem, in this sense, “reasonable”? If we can answer this question, even by a plausible guess, our interest in the problem increases and we can work better.
预见我们为之工作的结果的任何特征是好的。当我们对我们可以期待的东西有一些想法时，我们就会更清楚我们应该朝哪个方向走。现在，一个问题的一个重要特征是它所允许的解决方案的数量。最有趣的问题是那些只允许有一个解决方案的问题；我们倾向于认为具有唯一确定解决方案的问题是唯一 “合理” 的问题。在这个意义上，我们的问题是否 “合理”？如果我们能回答这个问题，哪怕是一个合理的猜测，我们对这个问题的兴趣就会增加，我们就能更好地工作。
Is our problem “reasonable”? This question is useful at an early stage of our work if we can answer it easily. If the answer is difficult to obtain, the trouble we have in obtaining it may outweigh the gain in interest. The same is true of the question “Is it possible to satisfy the condition?” and the allied questions of our list. We should put them because the answer might be easy and plausible, but we should not insist on them when the answer seems to be difficult or obscure.
我们的问题是否 “合理”？如果我们能轻易地回答这个问题，那么这个问题在我们工作的早期阶段是很有用的。如果答案难以获得，我们在获得答案时遇到的麻烦可能会超过利益上的收获。“有可能满足条件吗？”这个问题和我们清单上的相关问题也是如此。我们应该提出这些问题，因为答案可能是容易的、可信的，但当答案似乎是困难的或模糊的时候，我们就不应该坚持提出这些问题。
The corresponding questions for “problems to prove” are: Is it likely that the proposition is true? Or is it more likely that it is false? The way the question is put shows clearly that only a guess, a plausible provisional answer, is expected.
“需要证明的问题” 的相应问题是：。该命题可能是真的吗？还是更有可能是假的？这个问题的提出方式清楚地表明，人们只希望得到一个猜测，一个可信的临时答案。
Leibnitz, Gottfried Wilhelm (1646-1716), great mathematician and philosopher, planned to write an “Art of Invention” but he never carried through his plan. Numerous fragments dispersed in his works show, however, that he entertained interesting ideas about the subject whose importance he often emphasized. Thus, he wrote: “Nothing is more important than to see the sources of invention which are, in my opinion, more interesting than the inventions themselves.”
We are trying to prove a theorem, say, A. We are led to suspect another theorem, say, B; if B were true we could perhaps, using it, prove A. We assume B provisionally, postponing its proof, and go ahead with the proof of A. Such a theorem B is assumed, and is an auxiliary theorem to the originally proposed theorem A. Our little story is fairly typical and explains the present meaning of the word “lemma.”
我们试图证明一个定理，比如说，A。我们被引导去怀疑另一个定理，比如说，B；如果B是真的，我们也许可以用它来证明A。我们暂时假设B，推迟其证明，并继续进行A的证明。我们的小故事相当典型，解释了 “lemma” 这个词的现有含义。
Look at the unknown. This is old advice; the corresponding Latin saying is: “respice finem.” That is, look at the end. Remember your aim. Do not forget your goal. Think of what you are desiring to obtain. Do not lose sight of what is required. Keep in mind what you are working for. Look at the unknown. Look at the conclusion. The last two versions of “respice finem” are specifically adapted to mathematical problems, to “problems to find” and to “problems to prove” respectively.
Focusing our attention on our aim and concentrating our will on our purpose, we think of ways and means to attain it. What are the means to this end? How can you attain your aim? How can you obtain a result of this kind? What causes could produce such a result? Where have you seen such a result produced? What do people usually do to obtain such a result? And try to think of a familiar problem having the same or a similar unknown. And try to think of a familiar theorem having the same or a similar conclusion. Again, the last two versions are specifically adapted to “problems to find” and to “problems to prove” respectively.
1. We are going to consider mathematical problems, “problems to find,” and the suggestion: Try to think of a familiar problem having the same unknown. Let us compare this suggestion with that involved in the question: Do you know a related problem?
1. 我们要考虑数学问题，“要找的问题”，以及建议。试着想一个熟悉的问题，有相同的未知数。让我们把这个建议与问题中涉及的建议进行比较。你知道一个相关的问题吗？
The latter suggestion is more general than the former one. If a problem is related to another problem, the two have something in common; they may involve a few common objects or notions, or have some data in common, or some part of the condition, and so on. Our first suggestion insists on a particular common point: The two problems should have the same unknown. That is, the unknown should be in both cases an object of the same category, for instance, in both cases the length of a straight line.
后一个建议比前一个建议更普遍。如果一个问题与另一个问题有关，那么这两个问题就有一些共同点；它们可能涉及一些共同的对象或概念，或者有一些共同的数据，或者一些部分的条件，等等。我们的第一个建议是坚持一个特定的共同点。这两个问题应该有相同的未知数。也就是说，未知数在这两种情况下都应该是同一类别的物体，例如，在这两种情况下都是一条直线的长度。
In comparison with the general suggestion, there is a certain economy in the special suggestion.
与一般建议相比，特别建议有一定的经济性。
First, we may save some effort in representing the problem; we must not look at once at the whole problem but just at the unknown. The problem appears to us schematically, as
首先，我们可以在表现问题时节省一些精力；我们不能一下子看整个问题，而只是看未知的问题。这个问题对我们来说是一个示意图，如
Second, there is a certain economy of choice. Many, many problems may be related to the proposed problem, having some point or other in common with it. But, looking at the unknown, we restrict our choice; we take into consideration only such problems as have the same unknown. And, of course, among the problems having the same unknown, we consider first those which are the most elementary and the most familiar to us.
2. The problem before us has the form:
2. 我们面前的问题有这样的形式。
Now the simplest and most familiar problems of this kind are concerned with triangles: Given three constituent parts of a triangle find the length of a side. Remembering this, we have found something that may be relevant: Here is a problem related to yours and solved before. Could you use it? Could you use its result? In order to use the familiar results about triangles, we must have a triangle in our figure. Is there a triangle? Or should we introduce one in order to profit from those familiar results? Should you introduce some auxiliary element in order to make their use possible?
现在，这类问题中最简单和最熟悉的是关于三角形的问题。给出一个三角形的三个组成部分，找出一条边的长度。记住这一点，我们已经找到了可能相关的东西。这里有一个与你有关的问题，以前也解决过。你能使用它吗？你能使用它的结果吗？为了使用熟悉的关于三角形的结果，我们的图中必须有一个三角形。是否有一个三角形？或者我们应该引入一个，以便从这些熟悉的结果中获益？你是否应该引入一些辅助元素，以便使它们的使用成为可能？
There are several simple problems whose unknown is the side of a triangle. (They differ from each other in the data; two angles may be given and one side, or two sides and one angle, and the position of the angle with respect to the given sides may be different. Then, all these problems are particularly simple for right triangles.) With our attention riveted upon the problem before us, we try to find out which kind of triangle we should introduce, which formerly solved problem (with the same unknown as that before us) we could most conveniently adapt to our present purpose.
有几个简单的问题，其未知数是一个三角形的边。（它们在数据上有所不同；可能给出两个角和一条边，或两条边和一个角，而且角相对于给定边的位置可能不同。那么，对于直角三角形来说，所有这些问题都特别简单）。我们的注意力集中在我们面前的问题上，我们试图找出我们应该引入哪种三角形，哪一个以前解决的问题（与我们面前的未知数相同）我们可以最方便地适应我们现在的目的。
Having introduced a suitable auxiliary triangle, it may happen that we do not know yet three constituent parts of it. This, however, is not absolutely necessary; if we foresee that the missing parts can be obtained somehow we have made essential progress, we have a plan of the solution.
在引入了一个合适的辅助三角形后，可能会发生我们还不知道它的三个组成部分。然而，这并不是绝对必要的；如果我们预见到缺失的部分可以通过某种方式得到，我们就会取得基本的进展，我们就会有一个解决方案的计划。
3. The procedure sketched in the foregoing (under 1 and 2) is illustrated, essentially, by section 10 (the illustration is somewhat obscured by the slowness of the students). It is not difficult at all to add many similar examples. In fact, the solution of almost all “problems to find” usually proposed in less advanced classes can be started by proper use of the suggestion: And try to think of a familiar problem having the same or a similar unknown.
We must take such problems schematically, and look at the unknown first:
我们必须从原理上看待这样的问题，首先要看待未知的问题。
(1) Given . . . . . . . find the length of the line.
（1）给出 …… …… 求直线的长度。
(2) Given . . . . . . . find the angle.
（2）给出 …… …… 求角度。
(3) Given . . . . . . . find the volume of the tetrahedron.
（3）给出 …… …… 求四面体的体积。
(4) Given . . . . . . . construct the point.
（4）给出 …… …… …… …… …… …… …… …… …… …… …… ……
If we have some experience in dealing with elementary mathematical problems, we will readily recall some simple and familiar problem or problems having the same unknown. If the problem proposed is not one of those simple familiar problems we naturally try to make use of what is familiar to us and profit from the result of those simple problems. We try to introduce some useful well-known thing into the problem, and doing so we may get a good start.
如果我们有一些处理初级数学问题的经验，我们会很容易想起一些简单而熟悉的问题或具有相同未知数的问题。如果提出的问题不是那些简单熟悉的问题，我们自然会试图利用我们熟悉的东西，并从那些简单问题的结果中获益。我们试图在问题中引入一些有用的众所周知的东西，这样做我们可能会得到一个好的开始。
In each of the four cases mentioned there is an obvious plan, a plausible guess about the future course of the solution.
在提到的四个案例中，每一个都有一个明显的计划，一个关于解决方案的未来进程的合理猜测。
(1) The unknown should be obtained as a side of some triangle. It remains to introduce a suitable triangle with three known, or easily obtainable, constituents.
（1）未知数应作为某个三角形的边得到。剩下的就是介绍一个合适的三角形，它有三个已知的，或容易得到的成分。
(2) The unknown should be obtained as an angle in some triangle. It remains to introduce a suitable triangle.
（2）未知数应作为某个三角形中的一个角得到。这就需要引入一个合适的三角形。
(4) The unknown should be obtained as the intersection of two loci each of which is either a circle or a straight line. It remains to disentangle such loci from the proposed condition.
（4）未知数应作为两个地点的交点得到，每个地点都是一个圆或一条直线。现在要做的是，从所提出的条件中分离出这些坐标点。
In all these cases the plan is suggested by a simple problem with the same unknown and by the desire to use its result or its method. Pursuing such a plan, we may run into difficulties, of course, but we have some idea to start with which is a great advantage.
在所有这些情况下，计划都是由一个具有相同未知数的简单问题以及使用其结果或方法的愿望所提出的。追求这样的计划，我们当然会遇到困难，但我们有一些想法可以开始，这是一个很大的优势。
4. There is no such advantage if there is no formerly solved problem having the same unknown as the proposed problem. In such cases, it is much more difficult to tackle the proposed problem.
4. 如果没有以前解决的问题与提议的问题具有相同的未知性，那么就没有这种优势。在这种情况下，要解决所提出的问题就更难了。
“Find the area of the surface of a sphere with given radius.” This problem was solved by Archimedes. There is scarcely a simpler problem with the same unknown and there was certainly no such simpler problem of which Archimedes could have made use. In fact, Archimedes’ solution may be regarded as one of the most notable mathematical achievements.
“求给定半径的球体表面的面积”。这个问题是由阿基米德解决的。几乎没有比这更简单的未知数的问题，当然也没有比这更简单的问题阿基米德可以利用的。事实上，阿基米德的解决方案可以被认为是最显著的数学成就之一。
“Find the area of the surface of the sphere inscribed in a tetrahedron whose six edges are given.” If we know Archimedes’ result, we need not have Archimedes’ genius to solve the problem; it remains to express the radius of the inscribed sphere in terms of the six edges of the tetrahedron. This is not exactly easy but the difficulty cannot be compared with that of Archimedes’ problem.
“求刻在一个四面体中的球体表面的面积，该四面体的六条边已给定。” 如果我们知道阿基米德的结果，我们就不需要有阿基米德的天才来解决这个问题；剩下的就是用四面体的六条边来表示所刻球体的半径。这并不完全容易，但其难度无法与阿基米德的问题相比。
To know or not to know a formerly solved problem with the same unknown may make all the difference between an easy and a difficult problem.
知道或不知道一个以前解决过的具有相同未知数的问题，可能会使问题变得简单和困难。
5. When Archimedes found the area of the surface of the sphere he did not know, as we just mentioned, any formerly solved problem having the same unknown. But he knew various formerly solved problems having a similar unknown. There are curved surfaces whose area is easier to obtain than that of the sphere and which were well known in Archimedes’ time, as the lateral surfaces of right circular cylinders, of right circular cones, and of the frustums of such cones. We may be certain that Archimedes considered carefully these simpler similar cases. In fact, in his solution, he uses as approximation to the sphere a composite solid consisting of two cones and several frustums of cones (see DEFINITION, 6).
If we are unable to find a formerly solved problem having the same unknown as the problem before us, we try to find one having a similar unknown. Problems of the latter kind are less closely related to the problem before us than problems of the former kind and, therefore, less easy to use for our purpose in general but they may be valuable guides nevertheless.
如果我们无法找到一个以前解决的问题，其未知数与我们面前的问题相同，我们就试图找到一个具有类似未知数的问题。后一类问题与我们面前的问题的关系不如前一类问题密切，因此一般来说不容易用于我们的目的，但它们仍然可能是有价值的指导。
6. We add a few remarks concerning “problems to prove”; they are analogous to the foregoing more extensive comments on “problems to find.”
6. 我们补充一些关于 “需要证明的问题” 的评论；它们类似于前述关于 “需要发现的问题” 的更广泛的评论。
We have to prove (or disprove) a clearly stated theorem. Any theorem proved in the past which is in some way related to the theorem before us has a chance to be of some service. Yet we may expect the most immediate service of theorems which have the same conclusion as the one before us. Knowing this, we look at the conclusion, that is, we consider our theorem emphasizing the conclusion. Our way of looking at the theorem can be expressed in writing by a scheme as:
我们必须证明（或反驳）一个明确的定理。过去证明的任何定理，只要与我们面前的定理有某种联系，就有机会起到一定的作用。然而，我们可以期待那些与我们面前的定理有相同结论的定理提供最直接的服务。知道了这一点，我们就看结论，也就是说，我们考虑我们的定理，强调结论。我们看待定理的方式可以通过一个方案书面表达出来，即。
We focus our attention upon the conclusion before us and try to think of a familiar theorem having the same or a similar conclusion. Especially, we try to think of very simple familiar theorems of this sort.
我们把注意力集中在我们面前的结论上，并试着去想一个具有相同或类似结论的熟悉的定理。特别是，我们要试着想出这种非常简单的熟悉的定理。
In our case, there are various theorems of this kind and we may recollect the following: “If two triangles are congruent the corresponding angles are equal.” Here is a theorem related to yours and proved before. Could you use it? Should you introduce some auxiliary element in order to make its use possible?
Following these suggestions, and trying to judge the help afforded by the theorem we recollected, we may conceive a plan: Let us try to prove the equality of the angles in question from congruent triangles. We see that we must introduce a pair of triangles containing those angles and prove that they are congruent. Such a plan is certainly good to start the work and it may lead eventually to the desired end as in section 19.
根据这些建议，并试图判断我们所回忆的定理所提供的帮助，我们可以设想一个计划。让我们尝试用全等三角形来证明有关角的相等。我们看到，我们必须引入一对包含这些角的三角形并证明它们是全等的。这样的计划对于开始工作当然是好的，而且它最终可能会像第 19 节那样达到预期的结果。
7. Let us sum up. Recollecting formerly solved problems with the same or a similar unknown (formerly proved theorems with the same or a similar conclusion) we have a good chance to start in the right direction and we may conceive a plan of the solution. In simple cases, which are the most frequent in less advanced classes, the most elementary problems with the same unknown (theorems with the same conclusion) are usually sufficient. Trying to recollect problems with the same unknown is an obvious and common-sense device (compare what was said in this respect in section 4). It is rather surprising that such a simple and useful device is not more widely known; the author is inclined to think that it was not even stated before in full generality. In any case, neither students nor teachers of mathematics can afford to ignore the proper use of the suggestion: Look at the unknown! And try to think of a familiar problem having the same or a similar unknown.
7. 让我们来总结一下。回顾以前解决过的具有相同或类似未知数的问题（以前证明过的具有相同或类似结论的定理），我们有很好的机会在正确的方向上开始，我们可以构思一个解决的计划。在简单的情况下，也就是在不太高级的课程中最常见的情况下，具有相同未知数的最基本问题（具有相同结论的定理）通常就足够了。试图回忆具有相同未知数的问题是一种明显的常识性手段（比较一下第 4 节中关于这方面的内容）。令人惊讶的是，这样一个简单而有用的方法没有被更多的人知道；作者倾向于认为它以前甚至没有被完全概括地说明。在任何情况下，无论是学生还是数学教师都不能忽视对该建议的正确使用。看看未知的东西!并试着去想一个熟悉的问题，有相同或类似的未知数。
Modern heuristic endeavors to understand the process of solving problems, especially the mental operations typically useful in this process. It has various sources of information none of which should be neglected. A serious study of heuristic should take into account both the logical and the psychological background, it should not neglect what such older writers as Pappus, Descartes, Leibnitz, and Bolzano have to say about the subject, but it should least neglect unbiased experience. Experience in solving problems and experience in watching other people solving problems must be the basis on which heuristic is built. In this study, we should not neglect any sort of problem, and should find out common features in the way of handling all sorts of problems; we should aim at general features, independent of the subject matter of the problem. The study of heuristic has “practical” aims; a better understanding of the mental operations typically useful in solving problems could exert some good influence on teaching, especially on the teaching of mathematics.
The present book is a first attempt toward the realization of this program. We are going to discuss how the various articles of this Dictionary fit into the program.
本书是实现这一计划的第一次尝试。我们将讨论本词典的各条内容如何与该计划相适应。
1. Our list is, in fact, a list of mental operations typically useful in solving problems; the questions and suggestions listed hint at such operations. Some of these operations are described again in the Second Part, and some of them are more thoroughly discussed and illustrated in the First Part.
1. 事实上，我们的清单是一份通常对解决问题有用的心理操作清单；所列出的问题和建议都暗示了这种操作。其中一些操作将在第二部分中再次描述，其中一些操作在第一部分中得到了更彻底的讨论和说明。
For additional information about particular questions and suggestions of the list, the reader should refer to those fifteen articles of the Dictionary whose titles are the first sentences of the fifteen paragraphs of the list: WHAT IS THE UNKNOWN? IS IT POSSIBLE TO SATISFY THE CONDITION? DRAW A FIGURE. . . . CAN YOU USE THE RESULT? The reader, wishing information about a particular item of the list, should look at the first words of the paragraph in which the item is contained and then look up the article in the Dictionary that has those first words as title. For instance, the suggestion “Go back to definitions” is contained in the paragraph of the list whose first sentence is: COULD YOU RESTATE THE PROBLEM? Under this title, the reader finds a cross-reference to DEFINITION in which article the suggestion in question is explained and illustrated.
2. The process of solving problems is a complex process that has several different aspects. The twelve principal articles of this Dictionary study certain of these aspects at some length; we are going to mention their titles in what follows.
2. 解决问题的过程是一个复杂的过程，有几个不同的方面。本词典的十二篇主要文章对其中某些方面进行了详细的研究；我们将在下文中提到它们的标题。
When we are working intensively, we feel keenly the progress of our work; we are elated when our progress is rapid, we are depressed when it is slow. What is essential to PROGRESS AND ACHIEVEMENT in solving problems? The article discussing this question is often quoted in other parts of the Dictionary and should be read fairly early.
当我们深入工作时，我们会敏锐地感受到我们工作的进展；当我们的进展迅速时，我们会很高兴，当我们的进展缓慢时，我们会很沮丧。在解决问题的过程中，什么是进步和成就的关键？讨论这个问题的文章在《辞海》的其他部分经常被引用，应该相当早地阅读。
Trying to solve a problem, we consider different aspects of it in turn, we roll it over and over incessantly in our mind; VARIATION OF THE PROBLEM is essential to our work. We may vary the problem by DECOMPOSING AND RECOMBINING its elements, or by going back to the DEFINITION of certain of its terms, or we may use the great resources of GENERALIZATION, SPECIALIZATION, and ANALOGY. Variation of the problem may lead us to AUXILIARY ELEMENTS, or to the discovery of a more accessible AUXILIARY PROBLEM.
为了解决一个问题，我们依次考虑它的不同方面，我们在脑海中不断地翻来覆去；问题的变化对我们的工作至关重要。我们可以通过分解和重新组合其元素来改变问题，或者通过回到其某些术语的定义，或者我们可以使用通用化、专门化和模拟的巨大资源。问题的变化可能会使我们找到辅助元素，或者发现更容易获得的辅助问题。
We have to distinguish carefully between two kinds of problems, PROBLEMS TO FIND, PROBLEMS TO PROVE. Our list is specially adapted to “problems to find.” We have to revise it and change some of its questions and suggestions in order to apply it also to “problems to prove.”
我们必须仔细区分两种问题，即寻找的问题和证明的问题。我们的清单特别适用于 “寻找的问题”。我们必须修改它，改变其中的一些问题和建议，以便也适用于 “需要证明的问题”。
3. The process of solving problems has many aspects but some of them are not considered at all in this book and others only very briefly. It is justified, I think, to exclude from a first short exposition points which could appear too subtle, or too technical, or too controversial.
3. 解决问题的过程有很多方面，但有些方面在本书中根本没有考虑，有些方面只是非常简短地考虑。我认为，在第一篇简短的论述中排除那些可能显得过于微妙、或过于技术性、或过于有争议的观点是合理的。
Provisional, merely plausible HEURISTIC REASONING is important in discovering the solution, but you should not take it for a proof; you must guess, but also EXAMINE YOUR GUESS. The nature of heuristic arguments is discussed in SIGNS OF PROGRESS, but the discussion could go further.
临时的、仅仅是合理的启发式推理对于发现解决方案是很重要的，但你不应该把它当作证明；你必须猜测，但也要对你的猜测进行检查。启发式论证的性质在SIGNS OF PROGRESS中讨论过，但讨论可以更进一步。
The consideration of certain logical patterns is important in our subject but it appeared advisable not to introduce any technical article. There are only two articles predominantly devoted to psychological aspects, on DETERMINATION, HOPE, SUCCESS, and on SUBCONSCIENT WORK. There is an incidental remark on animal psychology; see WORKING BACKWARDS.
对某些逻辑模式的考虑在我们的主题中很重要，但似乎最好不要介绍任何技术性的文章。只有两篇文章主要致力于心理学方面，关于决心、希望、成功，以及关于潜心工作。有一篇关于动物心理学的附带评论；见《向后看》。
It is emphasized that all sorts of problems, especially PRACTICAL PROBLEMS, and even PUZZLES, are within the scope of heuristic. It is also emphasized that infallible RULES OF DISCOVERY are beyond the scope of serious research. Heuristic discusses human behavior in the face of problems; this has been in fashion, presumably, since the beginning of human society, and the quintessence of such ancient discussions seems to be preserved in the WISDOM OF PROVERBS.
我们强调，各种问题，特别是实际问题，甚至是难题，都属于启发式的范围。同时还强调，无懈可击的发现法则超出了严肃的研究范围。启发式讨论的是人类在面对问题时的行为；这大概从人类社会开始就一直在流行，这种古代讨论的精髓似乎被保存在谚语的智慧中。
4. A few articles on particular questions are included and some articles on more general aspects are expanded, because they could be, or parts of them could be, of special interest to students or teachers.
4. 一些关于特定问题的文章被包括在内，一些关于更普遍的方面的文章被扩展，因为它们可能是学生或教师特别感兴趣的，或其中的部分内容可能是。
There are articles discussing methodical questions often important in elementary mathematics, as PAPPUS, WORKING BACKWARDS (already quoted under 3), REDUCTIO AD ABSURDUM AND INDIRECT PROOF, INDUCTION AND MATHEMATICAL INDUCTION, SETTING UP EQUATIONS, TEST BY DIMENSION, and WHY PROOFS? A few articles address themselves more particularly to teachers, as ROUTINE PROBLEMS and DIAGNOSIS, and others to students somewhat more ambitious than the average, as THE INTELLIGENT PROBLEM-SOLVER, THE INTELLIGENT READER, and THE FUTURE MATHEMATICIAN.
It may be mentioned here that the dialogues between the teacher and his students, given in sections 8, 10, 18, 19, 20 and in various articles of the Dictionary may serve as models not only to the teacher who tries to guide his class but also to the problem-solver who works by himself. To describe thinking as “mental discourse,” as a sort of conversation of the thinker with himself, is not inappropriate. The dialogues in question show the progress of the solution; the problem-solver, talking with himself, may progress along a similar line.
这里可以提到的是，第 8、10、18、19、20 节和《辞海》各条中给出的教师和学生之间的对话，不仅可以作为试图指导其班级的教师的典范，也可以作为独自工作的问题解决者的典范。将思考描述为 “心理话语”，作为思考者与自己的一种对话，并无不妥之处。有关的对话显示了解决方案的进展；解决问题的人与自己对话，也可能沿着类似的路线进展。
5. We are not going to exhaust the remaining titles; just a few groups will be mentioned.
5. 我们不打算穷尽其余的头衔；只提几组。
Some articles contain remarks on the history of our subject, on DESCARTES, LEIBNITZ, BOLZANO, on HEURISTIC, on TERMS, OLD AND NEW and on PAPPUS (this last one has been quoted already under 4).
一些文章包含了对我们这个主题的历史、对德萨特、莱布尼茨、博尔扎诺、对赫里斯特克、对术语、旧的和新的以及对帕普斯的评论（这最后一篇已经在第 4 节中引用）。
A few articles explain technical terms: CONDITION, COROLLARY, LEMMA.
有几条解释技术术语。条件、推论、法则。
Some articles contain only cross-references (they are marked with daggers [†] in the Table of Contents).
有些文章只包含交叉引用（它们在目录中用匕首†标记）。
6. Heuristic aims at generality, at the study of procedures which are independent of the subject-matter and apply to all sorts of problems. The present exposition, however, quotes almost exclusively elementary mathematical problems as examples. It should not be overlooked that this is a restriction but it is hoped that this restriction does not impair seriously the trend of our study. In fact, elementary mathematical problems present all the desirable variety, and the study of their solution is particularly accessible and interesting. Moreover, nonmathematical problems although seldom quoted as examples are never completely forgotten. More advanced mathematical problems are never directly quoted but constitute the real background of the present exposition. The expert mathematician who has some interest for this sort of study can easily add examples from his own experience to elucidate the points illustrated by elementary examples here.
7. The writer of this book wishes to acknowledge his indebtedness and express his gratitude to a few modern authors, not quoted in the article on HEURISTIC. They are the physicist and philosopher Ernst Mach, the mathematician Jacques Hadamard, the psychologists William James and Wolfgang Köhler. He wishes also to quote the psychologist K. Duncker and the mathematician F. Krauss whose work (published after his own research was fairly advanced, and partly published) shows certain parallel remarks.
7. 本书作者希望承认他对一些现代作者的亏欠并表示感谢，在关于HEURISTIC的文章中没有引用。他们是物理学家和哲学家恩斯特·马赫、数学家雅克·哈达玛德、心理学家威廉·詹姆斯和沃尔夫冈·克勒。他还希望引用心理学家 K·Duncker 和数学家 F·Krauss，后者的工作（在他自己的研究相当先进之后发表，并部分出版）显示了某些平行的言论。
Notation. If you wish to realize the advantages of a well chosen and well known notation try to add a few not too small numbers with the condition that you are not allowed to use the familiar Arabic numerals, although you may use, if you wish to write, Roman numerals. Take, for instance, the numbers MMMXC, MDXCVI, MDCXLVI, MDCCLXXXI, MDCCCLXXXVII.
We can scarcely overestimate the importance of mathematical notation. Modern computers, using the decimal notation, have a great advantage over the ancient computers who did not have such a convenient manner of writing the numbers. An average modern student who is familiar with the usual notation of algebra, analytical geometry, and the differential and integral calculus, has an immense advantage over a Greek mathematician in solving the problems about areas and volumes which exercised the genius of Archimedes.
1. Speaking and thinking are closely connected, the use of words assists the mind. Certain philosophers and philologists went a little further and asserted that the use of words is indispensable to the use of reason.
1. 说话和思考是紧密相连的，文字的使用有助于思维的进行。某些哲学家和语言学家走得更远，断言言语的使用对理性的使用是不可缺少的。
Yet this last assertion appears somewhat exaggerated. If we have a little experience of serious mathematical work we know that we can do a piece of pretty hard thinking without using any words, just looking at geometric figures or manipulating algebraic symbols. Figures and symbols are closely connected with mathematical thinking, their use assists the mind. We could improve that somewhat narrow assertion of philosophers and philologists by bringing the words into line with other sorts of signs and saying that the use of signs appears to be indispensable to the use of reason.
然而，这最后的断言似乎有些夸张了。如果我们对严肃的数学工作有一点经验，我们就会知道，我们可以不使用任何语言，只看几何图形或操作代数符号，就能完成一块相当难的思考。数字和符号与数学思维密切相关，它们的使用有助于思维。我们可以改进哲学家和语言学家的这一有点狭隘的论断，把文字与其他种类的符号结合起来，说符号的使用似乎对理性的使用是不可缺少的。
At any rate, the use of mathematical symbols is similar to the use of words. Mathematical notation appears as a sort of language, une langue bien faite, a language well adapted to its purpose, concise and precise, with rules which, unlike the rules of ordinary grammar, suffer no exception.
不管怎么说，数学符号的使用与文字的使用是相似的。数学符号作为一种语言出现，une langue bien faite，一种很适合其目的的语言，简明而精确，其规则与普通语法规则不同，没有例外。
If we accept this viewpoint, SETTING UP EQUATIONS appears as a sort of translation, translation from ordinary language into the language of mathematical symbols.
如果我们接受这种观点，“建立方程” 似乎是一种翻译，从普通语言翻译成数学符号的语言。
2. Some mathematical symbols, as +, −, =, and several others, have a fixed traditional meaning, but other symbols, as the small and capital letters of the Roman and Greek alphabets, are used in different meanings in different problems. When we face a new problem, we must choose certain symbols, we have to introduce suitable notation. There is something analogous in the use of ordinary language. Many words are used in different meanings in different contexts; when precision is important, we have to choose our words carefully.
An important step in solving a problem is to choose the notation. It should be done carefully. The time we spend now on choosing the notation may be well repaid by the time we save later by avoiding hesitation and confusion. Moreover, choosing the notation carefully, we have to think sharply of the elements of the problem which must be denoted. Thus, choosing a suitable notation may contribute essentially to understanding the problem.
解决问题的一个重要步骤是选择记号。这个步骤应该谨慎进行。我们现在花在选择符号上的时间可能会因为以后避免了犹豫和混乱而得到很好的回报。此外，仔细选择符号，我们必须认真考虑问题中必须被表示的元素。因此，选择一个合适的符号可能对理解问题有很大的帮助。
3. A good notation should be unambiguous, pregnant, easy to remember; it should avoid harmful second meanings, and take advantage of useful second meanings; the order and connection of signs should suggest the order and connection of things.
3. 一个好的符号应该是不含糊的，包罗万象的，容易记忆的；它应该避免有害的第二含义，并利用有用的第二含义；符号的顺序和连接应该暗示事物的顺序和连接。
4. Signs must be, first of all, unambiguous. It is inadmissible that the same symbol denote two different objects in the same inquiry. If, solving a problem, you call a certain magnitude a you should avoid calling anything else a which is connected with the same problem. Of course, you may use the letter a in a different meaning in a different problem.
4. 符号首先必须是毫不含糊的。不允许同一个符号在同一个问题上表示两个不同的对象。如果在解决一个问题时，你把某个量级称为a，你应该避免把与同一问题有关的其他东西称为a。当然，你可以在不同的问题中以不同的含义使用字母a。
Although it is forbidden to use the same symbol for different objects it is not forbidden to use different symbols for the same object. Thus, the product of a and b may be written as
虽然禁止对不同的对象使用相同的符号，但不禁止对同一对象使用不同的符号。因此，a和b的乘积可以写成
5. A good sign should be easy to remember and easy to recognize; the sign should immediately remind us of the object and the object of the sign.
5. 一个好的标志应该是容易记忆和容易识别的；标志应该立即让我们想起标志的对象和对象的内容。
A simple device to make signs easily recognizable is to use initials as symbols. For example, in section 20 we used r for rate, t for time, V for volume. We cannot use, however, initials in all cases. Thus, in section 20, we had to consider a radius but we could not call it r because this letter was already taken to denote a rate. There are still other motives restricting the choice of symbols, and other means to make them easily recognizable which we are going to discuss.
使符号易于识别的一个简单方法是使用首字母作为符号。例如，在第 20 节，我们用r表示速率，t表示时间，V表示体积。然而，我们不能在所有情况下都使用首字母。因此，在第 20 节中，我们不得不考虑一个半径，但我们不能叫它r，因为这个字母已经被用来表示速率。还有其他限制符号选择的动机，以及其他使其易于识别的手段，我们将对此进行讨论。
6. Notation is not only easily recognizable but particularly helpful in shaping our conception when the order and connection of the signs suggest the order and connection of the objects. We need several examples to illustrate this point.
6. 当符号的顺序和联系暗示着对象的顺序和联系时，记号不仅容易识别，而且特别有助于塑造我们的概念。我们需要几个例子来说明这一点。
(I) In order to denote objects which are near to each other in the conception of the problem we use letters which are near to each other in the alphabet.
（I）为了表示在问题的概念中相互接近的对象，我们使用字母表中相互接近的字母。
Thus, we generally use letters at the beginning of the alphabet as a, b, c, for given quantities or constants, and letters at the end of the alphabet as x, y, z, for unknown quantities or variables.
因此，我们一般用字母开头的a、b、c表示给定的量或常数，用字母结尾的x、y、z表示未知的量或变量。
In section 8 we used a, b, c for the given length, width, and height of a parallelepiped. On this occasion, the notation a, b, c was preferable to the notation by initials l, w, h. The three lengths played the same role in the problem which is emphasized by the use of successive letters. Moreover, being at the beginning of the alphabet, a, b, c are, as we just said, the most usual letters to denote given quantities. On some other occasion, if the three lengths play different roles and it is important to know which lengths are horizontal and which one is vertical, the notation l, w, h might be preferable.
(II) In order to denote objects belonging to the same category, we frequently choose letters belonging to the same alphabet for one category, using different alphabets for different categories. Thus, in plane geometry we often use:
（二）为了表示属于同一类别的物体，我们经常为一个类别选择属于同一字母的字母，为不同类别使用不同的字母。因此，在平面几何中，我们经常使用。
Roman capitals as A, B, C, . . . for points,
small Roman letters as a, b, c, . . . for lines,
small Greek letters as α, β, γ, . . . for angles.
罗马大写字母A, B, C, …… 表示点，
小罗马字母a, b, c, …… 表示线，
小希腊字母α, β, γ, …… 表示角。
If there are two objects belonging to different categories but having some particular relation to each other which is important for our problem, we may choose, to denote these two objects, corresponding letters of the respective alphabets as A and a, B and b, and so on. A familiar example is the usual notation for a triangle:
如果有两个物体属于不同的类别，但彼此之间有某种特定的关系，这对我们的问题很重要，我们可以选择相应的字母来表示这两个物体，如A和a，B和b，等等。一个熟悉的例子是一个三角形的通常符号。
A, B, C stand for the vertices,
a, b, c for the sides,
α, β, γ for the angles.
A、B、C代表顶点，
a、b、c代表边，
α、β、γ代表角。
It is understood that a is the side opposite to the vertex A and the angle at A is called α.
可以理解为，a是与顶点A相对的边，A处的角称为α。
(III) In section 20, the letters a, b, x, y are particularly well chosen to indicate the nature and connection of the elements denoted. The letters a, b hint that the magnitudes denoted are constants; x, y indicate variables; a precedes b as x precedes y and this suggests that a is in the same relation to b as x is to y. In fact, a and x are horizontal, b and y vertical, and a : b = x : y.
（III）在第 20 节中，字母a、b、x、y的选择特别好，表明所表示的元素的性质和联系。字母a、b暗示所表示的大小是常数；x、y表示变量；a先于b，就像x先于y一样，这表明a与b的关系就像x与y的关系一样。事实上，a和x是水平的，b和y是垂直的，a：b=x：y。
7. The notation
7. 符号
indicates that the two triangles in question are similar. In modern books, the formula is meant to indicate that the two triangles are similar, the vertices corresponding to each other in the order as they are written, A to E, B to F, C to G. In older books, this proviso about the order was not yet introduced; the reader had to look at the figure or remember the derivation in order to ascertain which vertex corresponded to which.
The modern notation is much preferable to the older one. Using the modern notation, we may draw consequences from the formula without looking at the figure. Thus, we may derive that
现代的符号比老的符号要好得多。使用现代符号，我们可以从公式中得出结果，而不用看图。因此，我们可以推导出
and other relations of the same kind. The older notation expresses less and does not allow such definite consequences.
和其他同类的关系。旧的记号表达的内容较少，不允许有这样明确的后果。
A notation expressing more than another may be termed more pregnant. The modern notation for similitude of triangles is more pregnant than the older one, reflects the order and connection of things more fully than the older one, and therefore, it may serve as basis for more consequences than the older one.
一个符号比另一个符号表达的内容更多，可以称为更有内涵。现代的三角形模拟符号比旧的符号更有内涵，比旧的符号更充分地反映了事物的秩序和联系，因此，它可以作为比旧的符号更多的后果的基础。
8. Words have second meanings. Certain contexts in which a word is often used influence it and add something to its primary meaning, some shade, or second meaning, or “connotation.” If we write carefully, we try to choose among the words having almost the same meaning the one whose second meaning is best adapted.
8. 词语有第二含义。一个词经常被使用的某些语境会影响它，在它的主要意义上增加一些东西，一些阴影，或第二含义，或 “内涵”。如果我们认真写作，我们就会试着在具有几乎相同含义的词中选择其第二含义最适合的一个。
There is something similar in mathematical notation. Even mathematical symbols may acquire a sort of second meaning from contexts in which they are often used. If we choose our notation carefully, we have to take this circumstance into account. Let us illustrate the point.
数学符号中也有类似的东西。即使是数学符号也可能从它们经常被使用的环境中获得某种第二含义。如果我们仔细选择我们的符号，我们就必须考虑到这种情况。让我们来说明这一点。
There are certain letters which have acquired a firmly rooted, traditional meaning. Thus, e stands usually for the basis of natural logarithms, i for 
, the imaginary unit, and π for the ratio of the circumference of the circle to the diameter. It is on the whole better to use such symbols only in their traditional meaning. If we use such a symbol in some other meaning its traditional meaning could occasionally interfere and be embarrassing, even misleading. It is true that harmful second meanings of this sort give less trouble to the beginner who has not yet studied many subjects than to the mathematician who should have sufficient experience to deal with such nuisances.
Second meanings of the symbols can also be helpful, even very helpful, if they are used with tact. A notation used on former occasions may assist us in recalling some useful procedure; of course, we should be sufficiently careful to separate clearly the present (primary) meaning of the symbol from its former (secondary) meaning. A standing notation [as the traditional notation for the parts of the triangle which we mentioned before, 6 (II)] has great advantages; used on several former occasions it may assist us in recalling various formerly used procedures. We remember our formulas in some standing notation. Of course, we should be sufficiently careful when, owing to particular circumstances, we are obliged to use a standing notation in a meaning somewhat different from the usual one.
符号的第二含义也可以是有帮助的，甚至是非常有帮助的，如果它们被有技巧地使用。以前使用过的符号可以帮助我们回忆一些有用的程序；当然，我们应该足够小心，把符号的现在（主要）意义和以前（次要）意义明确分开。常设符号如我们之前提到的三角形各部分的传统符号，6（II）有很大的好处；在以前的几个场合使用，可以帮助我们回忆以前使用的各种程序。我们用一些常设的符号记住我们的公式。当然，当由于特殊情况，我们不得不使用与通常意义有些不同的常设符号时，我们应该足够小心。
9. When we have to choose between two notations, one reason may speak for one, and some other reason for the other. We need experience and taste to choose the more suitable notation as we need experience and taste to choose more suitable words. Yet it is good to know the various advantages and disadvantages discussed in the foregoing. At any rate, we should choose our notation carefully, and have some good reason for our choice.
9. 当我们必须在两种记号之间作出选择时，一种原因可能是支持一种，而另一种原因则是支持另一种。我们需要经验和品味来选择更合适的符号，就像我们需要经验和品味来选择更合适的词语一样。然而，了解前面所讨论的各种优点和缺点是很好的。无论如何，我们应该谨慎地选择我们的记号，并为我们的选择提供一些好的理由。
10. Not only the most hopeless boys in the class but also quite intelligent students may have an aversion for algebra. There is always something arbitrary and artificial about notation; to learn a new notation is a burden for the memory. The intelligent student refuses to assume the burden if he does not see any compensation for it. The intelligent student is justified in his aversion for algebra if he is not given ample opportunity to convince himself by his own experience that the language of mathematical symbols assists the mind. To help him to such experience is an important task of the teacher, one of his most important tasks.
I say that it is an important task but I do not say that it is an easy one. The foregoing remarks may be of some help. See also SETTING UP EQUATIONS. Checking a formula by extensive discussion of its properties may be recommended as a particularly instructive exercise; see section 14 and CAN YOU CHECK THE RESULT? 2.
我说这是一项重要的任务，但我并不说这是一项容易的任务。前面的评论可能会有一些帮助。请参阅《建立方程》。通过对公式属性的广泛讨论来检查公式可能被推荐为一个特别有启发性的练习；见第 14 节和你能检查结果吗？2.
Pappus, an important Greek mathematician, lived probably around A.D. 300. In the seventh book of his Collectiones, Pappus reports about a branch of study which he calls analyomenos. We can render this name in English as “Treasury of Analysis,” or as “Art of Solving Problems,” or even as “Heuristic”; the last term seems to be preferable here. A good English translation of Pappus’s report is easily accessible7; what follows is a free rendering of the original text:
帕普斯，一位重要的希腊数学家，大概生活在公元300 年左右。在他的Collectiones第七册中，帕普斯报告了一个研究的分支，他称之为analyomenos。我们可以把这个名字用英语翻译成 “分析的宝库”，或 “解决问题的艺术”，甚至 “启发式”；最后一个词在这里似乎更合适。帕普斯的报告有一个很好的英文翻译，很容易获得7以下是对原文的自由译文。
“The so-called Heuristic is, to put it shortly, a special body of doctrine for the use of those who, after having studied the ordinary Elements, are desirous of acquiring the ability to solve mathematical problems, and it is useful for this alone. It is the work of three men, Euclid, the author of the Elements, Apollonius of Perga, and Aristaeus the elder. It teaches the procedures of analysis and synthesis.
"所谓的启发式理论，简而言之，就是供那些在学习了普通的《元素》之后，希望获得解决数学问题的能力的人使用的一套特殊的学说，而且它只在这方面有用。它是三个人的作品，即《元素》的作者欧几里德、佩尔加的阿波罗尼乌斯和长者阿里斯泰乌斯。它教授了分析和综合的程序。
“In analysis, we start from what is required, we take it for granted, and we draw consequences from it, and consequences from the consequences, till we reach a point that we can use as starting point in synthesis. For in analysis we assume what is required to be done as already done (what is sought as already found, what we have to prove as true). We inquire from what antecedent the desired result could be derived; then we inquire again what could be the antecedent of that antecedent, and so on, until passing from antecedent to antecedent, we come eventually upon something already known or admittedly true. This procedure we call analysis, or solution backwards, or regressive reasoning.
“But in synthesis, reversing the process, we start from the point which we reached last of all in the analysis, from the thing already known or admittedly true. We derive from it what preceded it in the analysis, and go on making derivations until, retracing our steps, we finally succeed in arriving at what is required. This procedure we call synthesis, or constructive solution, or progressive reasoning.
"但是，在综合中，反过来说，我们从我们在分析中最后到达的那一点开始，从已经知道的或公认的真实的东西开始。我们从它那里推导出分析中的前述内容，并继续进行推导，直到回溯我们的步骤，我们最终成功地得出所需的内容。这种程序我们称之为综合，或建设性的解决方案，或渐进的推理。
“Now analysis is of two kinds; the one is the analysis of the ‘problems to prove’ and aims at establishing true theorems; the other is the analysis of the ‘problems to find’ and aims at finding the unknown.
"现在，分析有两种；一种是对 ‘需要证明的问题’ 的分析，目的是建立真正的定理；另一种是对 ‘需要寻找的问题’ 的分析，目的是寻找未知的问题。
“If we have a ‘problem to prove’ we are required to prove or disprove a clearly stated theorem A. We do not know yet whether A is true or false; but we derive from A another theorem B, from B another C, and so on, until we come upon a last theorem L about which we have definite knowledge. If L is true, A will be also true, provided that all our derivations are convertible. From L we prove the theorem K which preceded L in the analysis and, proceding in the same way, we retrace our steps; from C we prove B, from B we prove A, and so we attain our aim. If, however, L is false, we have proved A false.
“If we have a ‘problem to find’ we are required to find a certain unknown x satisfying a clearly stated condition. We do not know yet whether a thing satisfying such a condition is possible or not; but assuming that there is an x satisfying the condition imposed we derive from it another unknown y which has to satisfy a related condition; then we link y to still another unknown, and so on, until we come upon a last unknown z which we can find by some known method. If there is actually a z satisfying the condition imposed upon it, there will be also an x satisfying the original condition, provided that all our derivations are convertible. We first find z; then, knowing z, we find the unknown that preceded z in the analysis; proceeding in the same way, we retrace our steps, and finally, knowing y, we obtain x, and so we attain our aim. If, however, there is nothing that would satisfy the condition imposed upon z, the problem concerning x has no solution.”
“如果我们有一个 ‘要找的问题’，我们被要求找到某个满足明确规定条件的未知数x。我们还不知道满足这样一个条件的东西是否可能；但假设有一个满足条件的x，我们就从它引申出另一个必须满足相关条件的未知数y；然后我们把y和另一个未知数联系起来，以此类推，直到我们遇到一个我们可以通过某种已知方法找到的最后一个未知数z。如果实际上有一个z满足强加给它的条件，那么也会有一个x满足原来的条件，只要我们所有的推导都可以转换。我们首先找到z；然后，知道了z，我们在分析中找到z之前的未知数；以同样的方式进行，我们追溯我们的步骤，最后，知道了y，我们得到了x，于是我们达到了我们的目的。然而，如果没有任何东西可以满足强加在z身上的条件，那么关于x的问题就没有解决办法。
We should not forget that the foregoing is not a literal translation but a free rendering, a paraphrase. Various differences between the original and the paraphrase deserve comment, for Pappus’s text is important in many ways.
我们不应忘记，上述内容不是直译，而是自由译文，是一种意译。原文和译文之间的各种差异值得评论，因为帕普斯的文本在许多方面都很重要。
1. Our paraphrase uses a more definite terminology than the original and introduces the symbols A, B, . . . L, x, y, . . . z which the original has not.
1. 我们的译文使用了比原文更明确的术语，并引入了原文没有的符号A,B, …… L，x，y，…… z，而原文则没有。
2. The paraphrase has (p. 141, line 30) “mathematical problems” where the original means “geometrical problems.” This emphasizes that the procedures described by Pappus are by no means restricted to geometric problems; they are, in fact, not even restricted to mathematical problems. We have to illustrate this by examples since, in these matters, generality and independence from the nature of the subject are important (see section 3).
3. Algebraic illustration. Find x satisfying the equation
3.代数式说明。找到满足方程的x
This is a “problem to find,” not too easy for a beginner. He has to be familiar with the idea of analysis; not with the word “analysis” of course, but with the idea of attaining the aim by repeated reduction. Moreover, he has to be familiar with the simplest sorts of equations. Even with some knowledge, it takes a good idea, a little luck, a little invention to observe that, since 4∞ = (2∞)2 and 4−∞ = (2∞)−2, it may be advantageous to introduce
这是一个 “要找的问题”，对初学者来说不太容易。他必须熟悉分析的概念；当然不是 “分析” 这个词，而是熟悉通过反复还原达到目的的概念。此外，他还必须熟悉最简单的各种方程式。即使有一些知识，也需要一个好的想法，一点运气，一点发明来观察，因为 4∞=（2∞）2和4-∞=（2∞）-2，因此，引入以下内容可能是有利的
Now, this substitution is really advantageous, the equation obtained for y
现在，这种替换确实很有利，得到的y的方程是
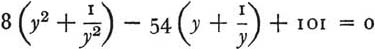
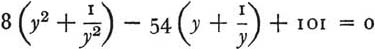
appears simpler than the original equation; but our task is not yet finished. It needs another little invention, another substitution
看起来比原来的方程简单；但我们的任务还没有完成。它需要另一个小发明，另一个替换
which transforms the condition into
这就把条件转化为
Here the analysis ends, provided that the problem-solver is acquainted with the solution of quadratic equations.
只要问题解决者熟悉二次方程的解法，分析就到此为止。
What is the synthesis? Carrying through, step by step, the calculations whose possibility was foreseen by the analysis. The problem-solver needs no new idea to finish his problem, only some patience and attention in calculating the various unknowns. The order of calculation is opposite to the order of invention; first z is found (z = 5/2, 17/4), then y (y = 2, 1/2, 4, 1/4), and finally the originally required x (x = 1, −1, 2, −2). The synthesis retraces the steps of the analysis, and it is easy to see in the present case why it does so.
4. Nonmathematical illustration. A primitive man wishes to cross a creek; but he cannot do so in the usual way because the water has risen overnight. Thus, the crossing becomes the object of a problem; “crossing the creek” is the x of this primitive problem. The man may recall that he has crossed some other creek by walking along a fallen tree. He looks around for a suitable fallen tree which becomes his new unknown, his y. He cannot find any suitable tree but there are plenty of trees standing along the creek; he wishes that one of them would fall. Could he make a tree fall across the creek? There is a great idea and there is a new unknown; by what means could he tilt the tree over the creek?
4.非数学插图。一个原始人想渡过一条小河；但他不能用通常的方法渡河，因为水在一夜之间上涨了。因此，渡河成为一个问题的对象；“渡河” 是这个原始问题的X。这个人可能记得，他曾经沿着一棵倒下的树走过其他的小溪。他四处寻找一棵合适的倒下的树，这就成了他的新的未知数，也就是他的y。他找不到任何合适的树，但小河边有很多树；他希望其中一棵树能倒下。他能不能让一棵树倒在小河对面？有一个伟大的想法，也有一个新的未知数；他能用什么方法让树倒在小河上？
This train of ideas ought to be called analysis if we accept the terminology of Pappus. If the primitive man succeeds in finishing his analysis he may become the inventor of the bridge and of the axe. What will be the synthesis? Translation of ideas into actions. The finishing act of the synthesis is walking along a tree across the creek.
如果我们接受帕普斯的术语，这一连串的想法应该被称为分析。如果原始人成功地完成了他的分析，他可能成为桥梁和斧头的发明者。综合将是什么？将思想转化为行动。综合的完成行为是沿着一棵树走过小河。
The same objects fill the analysis and the synthesis; they exercise the mind of the man in the analysis and his muscles in the synthesis; the analysis consists in thoughts, the synthesis in acts. There is another difference; the order is reversed. Walking across the creek is the first desire from which the analysis starts and it is the last act with which the synthesis ends.
同样的对象充满了分析和综合；它们在分析中锻炼人的头脑，在综合中锻炼人的肌肉；分析包括思想，综合包括行为。还有一个区别；顺序是相反的。走过小河是分析开始的第一个愿望，而它是综合结束的最后一个行为。
5. The paraphrase hints a little more distinctly than the original the natural connection between analysis and synthesis. This connection is manifest after the foregoing examples. Analysis comes naturally first, synthesis afterwards; analysis is invention, synthesis, execution; analysis is devising a plan, synthesis carrying through the plan.
6. The paraphrase preserves and even emphasizes certain curious phrases of the original: “assume what is required to be done as already done, what is sought as found, what you have to prove as true.” This is paradoxical; is it not mere self-deception to assume that the problem that we have to solve is solved? This is obscure; what does it mean? If we consider closely the context and try honestly to understand our own experience in solving problems, the meaning can scarcely be doubtful.
6. 释义保留了甚至强调了原文中某些奇怪的句子。“把需要做的事当作已经做了，把要找的事当作已经找到了，把你要证明的事当作真的”。这是自相矛盾的；假设我们必须解决的问题已经解决了，这难道不是单纯的自欺欺人吗？这是晦涩难懂的；它是什么意思？如果我们仔细考虑上下文，并诚实地尝试理解我们自己解决问题的经验，其含义几乎不会有任何疑问。
Let us first consider a “problem to find.” Let us call the unknown x and the data a, b, c. To “assume the problem as solved” means to assume that there exists an object x satisfying the condition—that is, having those relations to the data a, b, c which the condition prescribes. This assumption is made just in order to start the analysis, it is provisional, and it is harmless. For, if there is no such object and the analysis leads us anywhere, it is bound to lead us to a final problem that has no solution and hence it will be manifest that our original problem has no solution. Then, the assumption is useful. In order to examine the condition, we have to conceive, to represent to ourselves, or to visualize geometrically the relations which the condition prescribes between x and a, b, c; how could we do so without conceiving, representing, or visualizing x as existent? Finally, the assumption is natural. The primitive man whose thoughts and deeds we discussed in comment 4 imagines himself walking on a fallen tree and crossing the creek long before he actually can do so; he sees his problem “as solved.”
让我们首先考虑一个 “要找的问题”。让我们把未知数x和数据a、b、c称为 “假设问题已解决” 意味着假设存在一个满足条件的物体x，即具有条件所规定的与数据a、b、c的关系。这个假设只是为了开始分析，它是暂时的，也是无害的。因为，如果没有这样的对象，而分析又把我们引向任何地方，那么它必然会把我们引向一个没有解决办法的最终问题，从而表明我们原来的问题没有解决办法。那么，这个假设是有用的。为了考察条件，我们必须构思、向我们自己表示或以几何方式想象条件规定的x与a、b、c之间的关系；如果不构思、表示或想象x是存在的，我们怎么能做到这一点呢？最后，这个假设是自然的。我们在评论 4 中讨论的原始人的想法和行为，在他实际能够做到之前，早就想象自己走在倒下的树上，穿过小河；他认为他的问题 “已经解决”。
The object of a “problem to prove” is to prove a certain theorem A. The advice to “assume A as true” is just an invitation to draw consequences from the theorem A although we have not yet proved it. People with a certain mental character or a certain philosophy may shrink from drawing consequences from an unproved theorem; but such people cannot start an analysis.
Compare FIGURES, 2.
比较图，2。
7. The paraphrase uses twice the important phrase “provided that all our derivations are convertible”; see p. 142, line 33 and p. 143, lines 14–15. This is an interpolation; the original contains nothing of the sort and the lack of such a proviso was observed and criticized in modern times. See AUXILIARY PROBLEM, 6 for the notion of “convertible reduction.”
7. 释义中两次使用了重要的短语 “只要我们所有的衍生品都可以转换”；见第 142 页第 33 行和第 143 页第 14-15 行。这是一个插曲；原文中没有这样的内容，缺乏这样的但书在现代被观察和批评。关于 “可转换还原” 的概念，见《辅助问题》，6。
8. The “analysis of the problems to prove” is explained in the paraphrase in words quite different from those used by the original but there is no change in the sense; at any rate, there is no intention to change the sense. The analysis of the “problem to find,” however, is explained more concretely in the paraphrase than in the original. The original seems to aim at the description of a somewhat more general procedure, the construction of a chain of equivalent auxiliary problems which is described in AUXILIARY PROBLEM, 7.
8. 释义中对 “要证明的问题的分析” 的解释与原文的用词大不相同，但在意义上没有变化；无论如何，没有改变意义的意图。然而，对 “要找到的问题” 的分析，在译文中比在原文中解释得更具体一些。原文似乎旨在描述一个更普遍的程序，即在《辅助问题》中描述的构建一连串同等的辅助问题，7。
9. Many elementary textbooks of geometry contain a few remarks about analysis, synthesis, and “assuming the problem as solved.” There is little doubt that this almost ineradicable tradition goes back to Pappus, although there is hardly a current textbook whose writer would show any direct acquaintance with Pappus. The subject is important enough to be mentioned in elementary textbooks but easily misunderstood. The circumstance alone that it is restricted to textbooks of geometry shows a current lack of understanding; see comment 2 above. If the foregoing comments could contribute to a better understanding of this matter their length would be amply justified.
9. 许多几何学的初级教科书都包含了一些关于分析、综合和 “假设问题已解决” 的评论。毫无疑问，这个几乎不可改变的传统可以追溯到 Pappus，尽管目前几乎没有一本教科书的作者会显示出对 Pappus 的直接了解。这个主题很重要，足以在初级教科书中被提及，但却很容易被误解。仅仅是它被限制在几何学的教科书中这一情况就显示了目前对它的理解不足；见上文评论 2。如果前面的评论能够有助于更好地理解这个问题，那么它们的篇幅将是充分合理的。
Compare also REDUCTIO AD ABSURDUM AND INDIRECT PROOF, 2.
比较：REDUCTIO AD ABSURDUM 和 INDIRECT PROOF, 2.
1. To apply a rule to the letter, rigidly, unquestioningly, in cases where it fits and in cases where it does not fit, is pedantry. Some pedants are poor fools; they never did understand the rule which they apply so conscientiously and so indiscriminately. Some pedants are quite successful; they understood their rule, at least in the beginning (before they became pedants), and chose a good one that fits in many cases and fails only occasionally.
1. 在适合的情况下和不适合的情况下，死板地、不加怀疑地应用一条规则，就是迂腐。有些迂腐者是可怜的傻瓜；他们从未理解过他们如此认真和不加区别地应用的规则。有些迂腐者是相当成功的；他们至少在开始时（在他们成为迂腐者之前）就理解了他们的规则，并选择了一个好的规则，在很多情况下都适合，只是偶尔会失败。
To apply a rule with natural ease, with judgment, noticing the cases where it fits, and without ever letting the words of the rule obscure the purpose of the action or the opportunities of the situation, is mastery.
自然而然地运用一条规则，带着判断力，注意到它适合的情况，并且永远不要让规则的字句掩盖了行动的目的或情况的机会，这就是高手。
2. The questions and suggestions of our list may be helpful both to problem-solvers and to teachers. But, first, they must be understood, their proper use must be learned, and learned by trial and error, by failure and success, by experience in applying them. Second, their use should never become pedantic. You should ask no question, make no suggestion, indiscriminately, following some rigid habit. Be prepared for various questions and suggestions and use your judgment. You are doing a hard and exciting problem; the step you are going to try next should be prompted by an attentive and open-minded consideration of the problem before you. You wish to help a student; what you say to your student should proceed from a sympathetic understanding of his difficulties.
2. 我们清单上的问题和建议可能对问题解决者和教师都有帮助。但是，首先，必须理解它们，必须学习它们的正确用法，并且通过试验和错误，通过失败和成功，通过应用它们的经验来学习。第二，它们的使用决不应该变得迂腐。你不应该不分青红皂白地提出任何问题，提出任何建议，遵循某种僵化的习惯。要为各种问题和建议做好准备，并运用你的判断。你正在做一个艰难而激动人心的问题；你接下来要尝试的步骤应该由对你面前的问题的认真和开放的考虑所促使。你希望帮助一个学生；你对学生所说的话应该从对他的困难的同情理解出发。
Practical problems are different in various respects from purely mathematical problems, yet the principal motives and procedures of the solution are essentially the same. Practical engineering problems usually involve mathematical problems. We will say a few words about the differences, analogies, and connections between these two sorts of problems.
1. An impressive practical problem is the construction of a dam across a river. We need no special knowledge to understand this problem. In almost prehistoric times, long before our modern age of scientific theories, men built dams of some sort in the valley of the Nile, and in other parts of the world, where the crops depended on irrigation.
1. 一个令人印象深刻的实际问题是建造一座横跨河流的大坝。我们不需要特殊的知识来理解这个问题。几乎在史前时代，远在我们现代的科学理论时代之前，人们就在尼罗河流域和世界其他地区建造了某种水坝，那里的农作物依靠灌溉。
Let us visualize the problem of constructing an important modern dam.
让我们想象一下建造一个重要的现代大坝的问题。
What is the unknown? Many unknowns are involved in a problem of this kind: the exact location of the dam, its geometric shape and dimensions, the materials used in its construction, and so on.
什么是未知数？这类问题涉及许多未知数：大坝的确切位置，它的几何形状和尺寸，建造时使用的材料，等等。
What is the condition? We cannot answer this question in one short sentence because there are many conditions. In so large a project it is necessary to satisfy many important economic needs and to hurt other needs as little as possible. The dam should provide electric power, supply water for irrigation or the use of certain communities, and also help to control floods. On the other hand, it should disturb as little as possible navigation, or economically important fish-life, or beautiful scenery; and so forth. And, of course, it should cost as little as possible and be constructed as quickly as possible.
什么是条件？我们不能用一句简短的话来回答这个问题，因为有很多条件。在这么大的工程中，有必要满足许多重要的经济需求，并尽可能少地伤害其他需求。大坝应该提供电力，为灌溉或某些社区的使用提供水，还应该帮助控制洪水。另一方面，它应该尽可能少地干扰航行，或经济上重要的鱼类生活，或美丽的风景；等等。当然，它的成本应尽可能低，并尽可能快地建造。
What are the data? The multitude of desirable data is tremendous. We need topographical data concerning the vicinity of the river and its tributaries; geological data important for the solidity of foundations, possible leakage, and available materials of construction; meteorological data about annual precipitation and the height of floods; economic data concerning the value of ground which will be flooded, cost of materials and labor; and so on.
Our example shows that unknowns, data, and conditions are more complex and less sharply defined in a practical problem than in a mathematical problem.
我们的例子表明，在实际问题中，未知数、数据和条件比数学问题更复杂，定义也更不明确。
2. In order to solve a problem, we need a certain amount of previously acquired knowledge. The modern engineer has a highly specialized body of knowledge at his disposal, a scientific theory of the strength of materials, his own experience, and the mass of engineering experience stored in special technical literature. We cannot avail ourselves of such special knowledge here but we may try to imagine what was in the mind of an ancient Egyptian dam-builder.
2. 为了解决一个问题，我们需要一定量的以前获得的知识。现代工程师掌握着高度专业化的知识体系，有关于材料强度的科学理论，有他自己的经验，还有储存在特殊技术文献中的大量工程经验。我们不能在这里利用这种特殊的知识，但我们可以试着想象一下古埃及大坝建造者的想法是什么。
He has seen, of course, various other, perhaps smaller, dams: banks of earth or masonry holding back the water. He has seen the flood, laden with all sorts of debris, pressing against the bank. He might have helped to repair the cracks and the erosion left by the flood. He might have seen a dam break, giving way under the impact of the flood. He has certainly heard stories about dams withstanding the test of centuries or causing catastrophe by an unexpected break. His mind may have pictured the pressure of the river against the surface of the dam and the strain and stress in its interior.
当然，他也见过其他各种可能更小的水坝：用土或砖石筑成的堤岸挡住了水。他见过洪水，满载着各种碎石，压在岸边。他可能帮助修复了洪水留下的裂缝和侵蚀的痕迹。他可能见过水坝破裂，在洪水的冲击下让路。他肯定听说过大坝经受住了几个世纪的考验，或因意外断裂而造成灾难的故事。他的脑海中可能已经想象出河流对大坝表面的压力，以及大坝内部的应变和压力。
Yet the Egyptian dam-builder had no precise, quantitative, scientific concepts of fluid pressure or of strain and stress in a solid body. Such concepts form an essential part of the intellectual equipment of a modern engineer. Yet the latter also uses much knowledge which has not yet quite reached a precise, scientific level; what he knows about erosion by flowing water, the transportation of silt, the plasticity and other not quite clearly circumscribed properties of certain materials, is knowledge of a rather empirical character.
Our example shows that the knowledge needed and the concepts used are more complex and less sharply defined in practical problems than in mathematical problems.
我们的例子表明，在实际问题中，所需要的知识和使用的概念比数学问题更复杂，定义更不清晰。
3. Unknowns, data, conditions, concepts, necessary preliminary knowledge, everything is more complex and less sharp in practical problems than in purely mathematical problems. This is an important difference, perhaps the main difference, and it certainly implies further differences; yet the fundamental motives and procedures of the solution appear to be the same for both sorts of problems.
3. 未知数、数据、条件、概念、必要的初步知识，在实际问题中，一切都比纯数学问题更复杂，更不鲜明。这是一个重要的区别，也许是主要的区别，它当然也意味着进一步的区别；然而，对于这两种问题，解决的基本动机和程序似乎是相同的。
There is a widespread opinion that practical problems need more experience than mathematical problems. This may be so. Yet, very likely, the difference lies in the nature of the knowledge needed and not in our attitude toward the problem. In solving a problem of one or the other kind, we have to rely on our experience with similar problems and we often ask the questions: Have you seen the same problem in a slightly different form? Do you know a related problem?
有一种普遍的观点认为，实际问题比数学问题需要更多的经验。这可能是事实。然而，很可能的是，这种差异在于所需知识的性质，而不是我们对问题的态度。在解决这种或那种问题时，我们必须依靠我们对类似问题的经验，我们经常会问这样的问题。你是否以稍微不同的形式见过同样的问题？你知道一个相关的问题吗？
In solving a mathematical problem, we start from very clear concepts which are fairly well ordered in our mind. In solving a practical problem, we are often obliged to start from rather hazy ideas; then, the clarification of the concepts may become an important part of the problem. Thus, medical science is in a better position to check infectious diseases today than it was in the times before Pasteur when the notion of infection itself was rather hazy. Have you taken into account all essential notions involved in the problem? This is a good question for all sorts of problems but its use varies widely with the nature of the intervening notions.
In a perfectly stated mathematical problem all data and all clauses of the condition are essential and must be taken into account. In practical problems we have a multitude of data and conditions; we take into account as many as we can but we are obliged to neglect some. Take the case of the designer of a large dam. He considers the public interest and important economic interests but he is bound to disregard certain petty claims and grievances. The data of his problem are, strictly speaking, inexhaustible. For instance, he would like to know a little more about the geologic nature of the ground on which the foundations must be laid, but eventually he must stop collecting geologic data although a certain margin of uncertainty unavoidably remains.
在一个完美的数学问题中，所有的数据和条件的所有条款都是必要的，必须考虑到。在实际问题中，我们有大量的数据和条件；我们尽可能多地考虑到这些数据和条件，但我们不得不忽略一些。以一个大型水坝的设计者为例。他考虑到了公共利益和重要的经济利益，但他必然会忽略某些小的要求和不满。严格来说，他的问题的数据是取之不尽的。例如，他想多了解一点必须打地基的地面的地质性质，但最终他必须停止收集地质数据，尽管不可避免地存在一定的不确定性。
Did you use all the data? Did you use the whole condition? We cannot miss these questions when we deal with purely mathematical problems. In practical problems, however, we should put these questions in a modified form: Did you use all the data which could contribute appreciably to the solution? Did you use all the conditions which could influence appreciably the solution? We take stock of the available relevant information, we collect more information if necessary, but eventually we must stop collecting, we must draw the line somewhere, we cannot help neglecting something. “If you will sail without danger, you must never put to sea.” Quite often, there is a great surplus of data which have no appreciable influence on the final form of the solution.
你使用了所有的数据吗？你使用了整个条件吗？当我们处理纯粹的数学问题时，我们不能错过这些问题。然而，在实际问题中，我们应该把这些问题以一种修改过的形式提出来。你是否使用了所有可能对解决方案有明显贡献的数据？你是否使用了所有可能对解决方案产生明显影响的条件？我们评估现有的相关信息，必要时收集更多的信息，但最终我们必须停止收集，我们必须在某处划清界限，我们不能不忽略一些东西。“如果你想在没有危险的情况下航行，你必须永远不出海”。很多时候，有大量过剩的数据，对解决方案的最终形式没有明显的影响。
4. The designers of the ancient Egyptian dams had to rely on the common-sense interpretation of their experience, they had nothing else to rely on. The modern engineer cannot rely on common sense alone, especially if his project is of a new and daring design; he has to calculate the resistance of the projected dam, foresee quantitatively the strain and stress in its interior. For this purpose, he has to apply the theory of elasticity (which applies fairly well to constructions in concrete). To apply this theory, he needs a good deal of mathematics; the practical engineering problem leads to a mathematical problem.
This mathematical problem is too technical to be discussed here; all we can say about it is a general remark. In setting up and in solving mathematical problems derived from practical problems, we usually content ourselves with an approximation. We are bound to neglect some minor data and conditions of the practical problem. Therefore it is reasonable to allow some slight inaccuracy in the computations especially when we can gain in simplicity what we lose in accuracy.
这个数学问题技术性太强，在此不作讨论；我们能说的只是一个一般性的意见。在建立和解决由实际问题衍生出来的数学问题时，我们通常满足于近似值。我们必然会忽略实际问题的一些小数据和条件。因此，在计算中允许一些轻微的不准确是合理的，特别是当我们可以在简单性上获得我们在准确性上的损失时。
5. Much could be said about approximations that would deserve general interest. We cannot suppose, however, any specialized mathematical knowledge and therefore we restrict ourselves to just one intuitive and instructive example.
5. 关于近似值，可以说很多，值得普遍关注。然而，我们不能假设有任何专门的数学知识，因此我们只限于一个直观的、有启发性的例子。
The drawing of geographic maps is an important practical problem. Devising a map, we often assume that the earth is a sphere. Now this is only an approximate assumption and not the exact truth. The surface of the earth is not at all a mathematically defined surface and we definitely know that the earth is flattened at the poles. Assuming, however, that the earth is a sphere, we may draw a map of it much more easily. We gain much in simplicity and do not lose a great deal in accuracy. In fact, let us imagine a big ball that has exactly the shape of the earth and that has a diameter of 25 feet at its equator. The distance between the poles of such a ball is less than 25 feet because the earth is flattened, but only about one inch less. Thus the sphere yields a good practical approximation.
1. The aim of a “problem to find” is to find a certain object, the unknown of the problem.
1. 寻找问题 "的目的是要找到某个对象，即问题的未知数。
The unknown is also called “quaesitum,” or the thing sought, or the thing required. “Problems to find” may be theoretical or practical, abstract or concrete, serious problems or mere puzzles. We may seek all sorts of unknowns; we may try to find, to obtain, to acquire, to produce, or to construct all imaginable kinds of objects. In the problem of the mystery story the unknown is a murderer. In a chess problem the unknown is a move of the chessmen. In certain riddles the unknown is a word. In certain elementary problems of algebra the unknown is a number. In a problem of geometric construction the unknown is a figure.
未知数也被称为 “quaesitum”，或被寻找的东西，或被要求的东西。“要找的问题” 可能是理论的或实际的，抽象的或具体的，严重的问题或仅仅是困惑。我们可以寻找各种未知的东西；我们可以尝试寻找、获得、获取、生产或建造所有可以想象的各种物体。在神秘故事的问题中，未知数是一个谋杀犯。在一个国际象棋问题中，未知数是棋手的一步棋。在某些谜语中，未知数是一个词。在某些初级的代数问题中，未知数是一个数字。在一个几何结构的问题中，未知数是一个数字。
2. The aim of a “problem to prove” is to show conclusively that a certain clearly stated assertion is true, or else to show that it is false. We have to answer the question: Is this assertion true or false? And we have to answer conclusively, either by proving the assertion true, or by proving it false.
2. 证明问题 "的目的是要最终证明某个明确的断言是真的，否则就证明它是假的。我们必须回答这个问题。这个论断是真的还是假的？我们必须做出结论性的回答，要么证明这个论断是真的，要么证明它是假的。
A witness affirms that the defendant stayed at home a certain night. The judge has to find out whether this assertion is true or not and, moreover, he has to give as good grounds as possible for his finding. Thus, the judge has a “problem to prove.” Another “problem to prove” is to “prove the theorem of Pythagoras.” We do not say: “Prove or disprove the theorem of Pythagoras.” It would be better in some respects to include in the statement of the problem the possibility of disproving, but we may neglect it, because we know that the chances for disproving the theorem of Pythagoras are rather slight.
3. The principal parts of a “problem to find” are the unknown, the data, and the condition.
3. 一个 “要找的问题” 的主要部分是未知数、数据和条件。
If we have to construct a triangle with sides a, b, c, the unknown is a triangle, the data are the three lengths a, b, c, and the triangle is required to satisfy the condition that its sides have the given lengths a, b, c. If we have to construct a triangle whose altitudes are a, b, c, the unknown is an object of the same category as before, the data are the same, but the condition linking the unknown to the data is different.
如果我们要构造一个边长为 a、b、c的三角形，未知数是一个三角形，数据是三个长度a、b、c，要求三角形满足其边长为a、b、c的条件；如果我们要构造一个高度为a、b、c的三角形，未知数是一个与之前相同的物体，数据是相同的，但将未知数与数据联系起来的条件是不同的。
4. If a “problem to prove” is a mathematical problem of the usual kind, its principal parts are the hypothesis and the conclusion of the theorem which has to be proved or disproved.
4. 如果一个 “要证明的问题” 是一个通常的数学问题，它的主要部分是假设和需要证明或反驳的定理结论。
“If the four sides of a quadrilateral are equal, then the two diagonals are perpendicular to each other.” The second part starting with “then” is the conclusion, the first part starting with “if” is the hypothesis.
“如果一个四边形的四条边相等，那么两条对角线就互相垂直。” 以 “那么” 开头的第二部分是结论，以 “如果” 开头的第一部分是假说。
[Not all mathematical theorems can be split naturally into hypothesis and conclusion. Thus, it is scarcely possible to split so the theorem: “There are an infinity of prime numbers.”]
并非所有的数学定理都可以自然地拆分为假设和结论。因此，几乎不可能这样拆分定理。“有无数个质数。”
5. If you wish to solve a “problem to find” you must know, and know very exactly, its principal parts, the unknown, the data, and the condition. Our list contains many questions and suggestions concerned with these parts.
5. 如果你想解决一个 “要找的问题”，你必须知道，并且非常准确地知道它的主要部分，未知数、数据和条件。我们的清单包含了许多与这些部分有关的问题和建议。
What is the unknown? What are the data? What is the condition?
未知数是什么？数据是什么？条件是什么？
Separate the various parts of the condition.
将病情的各个部分分开。
Find the connection between the data and the unknown.
找到数据和未知数之间的联系。
Keep only a part of the condition, drop the other part; how far is the unknown then determined, how can it vary? Could you derive something useful from the data? Could you think of other data appropriate to determine the unknown? Could you change the unknown, or the data, or both if necessary, so that the new unknown and the new data are nearer to each other?
只保留一部分条件，放弃另一部分；那么未知数在多大程度上是确定的，它可以如何变化？你能从这些数据中得出一些有用的东西吗？你能想到其他适合确定未知数的数据吗？你能不能改变未知数或数据，或必要时两者都改变，使新的未知数和新的数据更接近？
Did you use all the data? Did you use the whole condition?
你使用了所有的数据吗？你使用了整个条件吗？
6. If you wish to solve a “problem to prove” you must know, and know very exactly, its principal parts, the hypothesis, and the conclusion. There are useful questions and suggestions concerning these parts which correspond to those questions and suggestions of our list which are specially adapted to “problems to find.”
6. 如果你想解决一个 “需要证明的问题”，你必须知道，并且非常准确地知道它的主要部分、假设和结论。关于这些部分有一些有用的问题和建议，这些问题和建议与我们清单中特别适合于 “寻找问题” 的问题和建议相对应。
What is the hypothesis? What is the conclusion?
假设是什么？结论是什么？
Separate the various parts of the hypothesis.
将假设的各个部分分开。
Find the connection between the hypothesis and the conclusion.
找到假设和结论之间的联系。
Look at the conclusion! And try to think of a familiar theorem having the same or a similar conclusion.
看看这个结论吧!试着想一想一个熟悉的定理有相同或类似的结论。
Keep only a part of the hypothesis, drop the other part; is the conclusion still valid? Could you derive something useful from the hypothesis? Could you think of another hypothesis from which you could easily derive the conclusion? Could you change the hypothesis, or the conclusion, or both if necessary, so that the new hypothesis and the new conclusion are nearer to each other?
只保留假说的一部分，放弃另一部分；结论仍然有效吗？你能从这个假说中得出一些有用的东西吗？你能想出另一个假设，从中轻松得出结论吗？你能不能改变假说或结论，或者必要时两者都改变，使新的假说和新的结论更接近于彼此？
Did you use the whole hypothesis?
你使用了整个假说吗？
Progress and achievement. Have you made any progress? What was the essential achievement? We may address questions of this kind to ourselves when we are solving a problem or to a student whose work we supervise. Thus, we are used to judge, more or less confidently, progress and achievement in concrete cases. The step from such concrete cases to a general description is not easy at all. Yet we have to undertake this step if we wish to make our study of heuristic somewhat complete and we must try to clarify what constitutes, in general, progress and achievement in solving problems.
1. In order to solve a problem, we must have some knowledge of the subject-matter and we must select and collect the relevant items of our existing but initially dormant knowledge. There is much more in our conception of the problem at the end than was in it at the outset; what has been added? What we have succeeded in extracting from our memory. In order to obtain the solution we have to recall various essential facts. We have to recollect formerly solved problems, known theorems, definitions, if our problem is mathematical. Extracting such relevant elements from our memory may be termed mobilization.
1. 为了解决一个问题，我们必须有一些关于主题事项的知识，我们必须选择和收集我们现有的但最初沉睡的知识中的相关项目。最后，我们对问题的概念比一开始的概念多得多；增加了什么？我们已经成功地从我们的记忆中提取了什么。为了获得解决方案，我们必须回忆各种基本事实。如果我们的问题是数学问题，我们必须回忆以前解决过的问题、已知的定理、定义。从我们的记忆中提取这些相关的元素可以被称为调动。
2. In order to solve a problem, however, it is not enough to recollect isolated facts, we must combine these facts, and their combination must be well adapted to the problem at hand. Thus, in solving a mathematical problem, we have to construct an argument connecting the materials recollected to a well adapted whole. This adapting and combining activity may be termed organization.
2. 然而，为了解决一个问题，仅仅回忆孤立的事实是不够的，我们必须把这些事实结合起来，而且它们的结合必须与手头的问题相适应。因此，在解决一个数学问题时，我们必须构建一个论据，将所回忆的材料连接成一个合适的整体。这种调整和组合的活动可以称为组织。
Mobilization and organization are but two aspects of the same complex process which has still many other aspects.
动员和组织只是同一个复杂过程的两个方面，这个过程还有许多其他方面。
4. Another aspect of the progress of our work is that our mode of conception changes. Enriched with all the materials which we have recalled, adapted to it, and worked into it, our conception of the problem is much fuller at the end than it was at the outset. Desiring to proceed from our initial conception of the problem to a more adequate, better adapted conception, we try various standpoints and view the problem from different sides. We could make hardly any progress without VARIATION OF THE PROBLEM.
4. 我们工作进展的另一个方面是，我们的构思模式发生了变化。由于我们回顾了所有的材料，对其进行了调整，并在其中进行了工作，我们对问题的概念在结束时要比一开始时更充分。我们希望从最初的问题概念发展到一个更充分、更合适的概念，因此我们尝试了各种立场，并从不同的角度看待这个问题。如果没有问题的变化，我们几乎不可能取得任何进展。
5. As we progress toward our final goal we see more and more of it, and when we see it better we judge that we are nearer to it. As our examination of the problem advances, we foresee more and more clearly what should be done for the solution and how it should be done. Solving a mathematical problem we may foresee, if we are lucky, that a certain known theorem might be used, that the consideration of a certain formerly solved problem might be helpful, that going back to the meaning of a certain technical term might be necessary. We do not foresee such things with certainty, only with a certain degree of plausibility. We shall attain complete certainty when we have obtained the complete solution, but before obtaining certainty we must often be satisfied with a more or less plausible guess. Without considerations which are only plausible and provisional, we could never find the solution which is certain and final. We need HEURISTIC REASONING.
5. 随着我们向最终目标的迈进，我们看到了越来越多的目标，当我们看得更清楚时，我们判断我们更接近它了。随着我们对问题研究的深入，我们越来越清楚地预见到应该做什么来解决这个问题，以及应该如何做。在解决一个数学问题时，如果我们幸运的话，我们可能会预见到，某个已知的定理可能会被使用，对某个以前解决的问题的考虑可能会有帮助，回到某个技术术语的含义可能是必要的。我们不能肯定地预见这些事情，只能说有一定程度的可信性。当我们获得完整的解决方案时，我们将获得完全的确定性，但在获得确定性之前，我们往往必须满足于或多或少的可信的猜测。如果没有似是而非和临时性的考虑，我们永远无法找到确定和最终的解决方案。我们需要理性的推理。
6. What is progress toward the solution? Advancing mobilization and organization of our knowledge, evolution of our conception of the problem, increasing prevision of the steps which will constitute the final argument. We may advance steadily, by small imperceptible steps, but now and then we advance abruptly, by leaps and bounds. A sudden advance toward the solution is called a BRIGHT IDEA, a good idea, a happy thought, a brain-wave (in German there is a more technical term, Einfall). What is a bright idea? An abrupt and momentous change of our outlook, a sudden reorganization of our mode of conceiving the problem, a just emerging confident prevision of the steps we have to take in order to attain the solution.
7. The foregoing considerations provide the questions and suggestions of our list with the right sort of background.
7. 上述考虑为我们清单上的问题和建议提供了正确的背景。
Many of these questions and suggestions aim directly at the mobilization of our formerly acquired knowledge: Have you seen it before? Or have you seen the same problem in a slightly different form? Do you know a related problem? Do you know a theorem that could be useful? Look at the unknown! And try to think of a familiar problem having the same or a similar unknown.
其中许多问题和建议的目的是直接调动我们以前获得的知识。你以前见过这个问题吗？或者你是否以稍微不同的形式见过同样的问题？你知道一个相关的问题吗？你知道一个可能有用的定理吗？看看这个未知数吧!试着去想一个熟悉的问题，有相同或相似的未知数。
There are typical situations in which we think that we have collected the right sort of material and we work for a better organization of what we have mobilized: Here is a problem related to yours and solved before. Could you use it? Could you use its result? Could you use its method? Should you introduce some auxiliary element in order to make its use possible?
在一些典型的情况下，我们认为我们已经收集了正确的材料，我们努力将我们所动员的东西更好地组织起来。这里有一个与你有关的问题，以前也解决过。你可以使用它吗？你能使用它的结果吗？你能使用它的方法吗？你是否应该引入一些辅助元素，以使其使用成为可能？
There are other typical situations in which we think that we have not yet collected enough material. We wonder what is missing: Did you use all the data? Did you use the whole condition? Have you taken into account all essential notions involved in the problem?
还有一些典型的情况，我们认为我们还没有收集到足够的材料。我们想知道缺少什么。你使用了所有的数据吗？你使用了整个条件吗？你是否考虑到了问题中涉及的所有基本概念？
Some questions aim directly at the variation of the problem: Could you restate the problem? Could you restate it still differently? Many questions aim at the variation of the problem by specified means, as going back to the DEFINITION, using ANALOGY, GENERALIZATION, SPECIALIZATION, DECOMPOSING AND RECOMBINING.
Still other questions suggest a trial to foresee the nature of the solution we are striving to obtain: Is it possible to satisfy the condition? Is the condition sufficient to determine the unknown? Or is it insufficient? Or redundant? Or contradictory?
还有一些问题建议进行试验，预见我们努力获得的解决方案的性质：是否有可能满足条件？该条件是否足以确定未知数？还是不充分？或者是多余的？或者是矛盾的？
The questions and suggestions of our list do not mention directly the bright idea; but, in fact, all are concerned with it. Understanding the problem we prepare for it, devising a plan we try to provoke it, having provoked it we carry it through, looking back at the course and the result of the solution we try to exploit it better.8
我们清单上的问题和建议并没有直接提到光明的想法；但事实上，所有的问题都与它有关。了解了问题，我们就为它做准备；制定了计划，我们就努力去激起它；激起了它，我们就实施它；回顾解决问题的过程和结果，我们就努力更好地利用它。8
Take, for instance, the words
举例来说，以下这句话
The problem is to find an “anagram,” that is, a rearrangement of the letters contained in the given words into one word. It is interesting to observe that, when we are solving this puzzle, several questions of our list are pertinent and even stimulating.
问题是要找到一个 “变位词”，也就是把给定单词中包含的字母重新排列成一个单词。有趣的是，当我们在解决这个谜题时，我们清单上的几个问题是相关的，甚至是刺激性的。
What is the unknown? A word.
未知是什么？一个词。
What are the data? The four words DRY OXTAIL IN REAR.
这些数据是什么？后面的四个字 “干氧”。
Draw a figure. It is quite useful to mark out fifteen blank spaces:
画一个图。标出 15 个空白处是相当有用的。
Could you restate the problem? We have to find a word containing, in some arrangement, the letters
你能重述一下这个问题吗？我们必须找到一个包含以下字母的词，以某种方式排列
This is certainly an equivalent restatement of the problem (see AUXILIARY PROBLEM, 6). It may be an advantageous restatement. Separating the vowels from the consonants (this is important, the alphabetical order is not) we see another aspect of the problem. Thus, we see now that the desired word has seven syllables unless it has some diphthongs.
这当然是对问题的等同重述（见辅助问题，6）。这可能是一个有利的重述。把元音和辅音分开（这很重要，字母顺序并不重要），我们看到问题的另一个方面。因此，我们现在看到，所需的词有七个音节，除非它有一些双元音。
If you cannot solve the proposed problem, try to solve first some related problem. A related problem is to form words with some of the given letters. We can certainly form short words of this kind. Then we try to find longer and longer words. The more letters we use the nearer we may come to the desired word.
如果你不能解决所提出的问题，请先尝试解决一些相关问题。一个相关的问题是用一些给定的字母组成单词。我们当然可以组成这样的短词。然后，我们尝试找到更长更长的单词。我们使用的字母越多，就可能越接近所需的单词。
Could you solve a part of the problem? The desired word is so long that it must have distinct parts. It is, probably, a compound word, or it is derived from some other word by adding some usual ending. Which usual ending could it be?
你能解决一部分的问题吗？所需的词太长了，它必须有不同的部分。它很可能是一个复合词，或者是通过添加一些通常的结尾从其他词中衍生出来的。它可能是哪个通常的结尾？
Keep only a part of the condition and drop the other part. We may try to think of a long word with, possibly, as many as seven syllables and relatively few consonants, containing an X and a Y.
只保留条件的一部分，放弃另一部分。我们可以试着想一个长词，可能有多达七个音节，辅音相对较少，包含一个 X 和一个 Y。
The questions and suggestions of our list cannot work magic. They cannot give us the solution of all possible puzzles without any effort on our part. If the reader wishes to find the word, he must keep on trying and thinking about it. What the questions and suggestions of the list can do is to “keep the ball rolling.” When, discouraged by lack of success, we are inclined to drop the problem, they may suggest to us a new trial, a new aspect, a new variation of the problem, a new stimulus; they may keep us thinking.
For another example see DECOMPOSING AND RECOMBINING, 8.
另一个例子见《解构与重组》，8。
Reductio ad absurdum shows the falsity of an assumption by deriving from it a manifest absurdity. “Reduction to an absurdity” is a mathematical procedure but it has some resemblance to irony which is the favorite procedure of the satirist. Irony adopts, to all appearance, a certain opinion and stresses it and overstresses it till it leads to a manifest absurdity.
荒诞还原法通过从一个假设中推导出一个明显的荒诞性来说明这个假设的虚假性。“还原为荒谬” 是一个数学程序，但它与讽刺有一些相似之处，而讽刺是讽刺者最喜欢的程序。讽刺在所有的表面上采用某种观点，并强调它，过度强调它，直到它导致一个明显的荒谬。
Indirect proof establishes the truth of an assertion by showing the falsity of the opposite assumption. Thus, indirect proof has some resemblance to a politician’s trick of establishing a candidate by demolishing the reputation of his opponent.
间接证明通过显示相反假设的虚假性来确立一个论断的真实性。因此，间接证明在某种程度上类似于政治家通过破坏对手的声誉来确立候选人的伎俩。
Both “reductio ad absurdum” and indirect proof are effective tools of discovery which present themselves naturally to an intent mind. Nevertheless, they are disliked by a few philosophers and many beginners, which is understandable; satirical people and tricky politicians do not appeal to everybody. We shall first illustrate the effectiveness of both procedures by examples and discuss objections against them afterwards.
“归谬法” 和间接证明都是有效的发现工具，它们自然而然地呈现在一个有意图的头脑中。然而，它们被一些哲学家和许多初学者所厌恶，这是可以理解的；讽刺性的人和狡猾的政治家并不吸引所有人。我们将首先通过例子说明这两种程序的有效性，然后讨论反对它们的意见。
We may learn something by trying to solve this puzzle whose statement demands some elucidation.
通过尝试解决这个谜题，我们可能会学到一些东西，这个谜题的陈述需要一些阐释。
What is the unknown? A set of numbers; and by numbers we mean here, of course, ordinary integers.
未知数是什么？一组数字；当然，我们这里指的是普通的整数。
What is given? The number 100.
给出了什么？数字 100。
What is the condition? The condition has two parts. First, writing the desired set of numbers, we must use each of the ten digits, 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9, just once. Second, the sum of all numbers in the set must be 100.
什么是条件？这个条件有两个部分。首先，写出所需的一组数字，我们必须使用十个数字中的每一个，0，1，2，3，4，5，6，7，8 和 9，只用一次。第二，这组数字的总和必须是 100。
Keep only a part of the condition, drop the other part. The first part alone is easy to satisfy. Take the set 19, 28, 37, 46, 50; each figure occurs just once. But, of course, the second part of the condition is not satisfied; the sum of these numbers is 180, not 100. We could, however, do better. “Try, try again.” Yes,
只保留条件的一部分，放弃另一部分。仅仅是第一部分就很容易满足。以 19、28、37、46、50 为例；每个数字只出现一次。但是，当然，条件的第二部分并没有得到满足；这些数字的总和是 180，而不是 100。不过，我们可以做得更好。“试试，再试试。” 是的。
The first part of the condition is satisfied, and the second part is almost satisfied; we have 99 instead of 100. Of course, we can easily satisfy the second part if we drop the first:
条件的第一部分得到了满足，第二部分也几乎得到了满足；我们有 99 而不是 100。当然，如果我们放弃第一部分，我们可以很容易地满足第二部分。
The first part is not satisfied: the figure 1 occurs twice, and 0 not at all; the other figures are all right. “Try, try again.”
第一部分没有得到满足：数字 1出现了两次，而 0 根本没有出现；其他数字都是正确的。“试试，再试试。”
After a few unsuccessful trials, however, we may be led to suspect that it is not possible to obtain 100 in the manner required. Eventually the problem arises: Prove that it is impossible to satisfy both parts of the proposed condition at the same time.
然而，经过几次不成功的试验后，我们可能会怀疑不可能以所需的方式获得 100。最终，问题出现了。证明不可能同时满足拟议条件的两个部分。
We suspect that this situation cannot actually arise and our suspicion, based on the experience of our unsuccessful trials, has some foundation. Nevertheless, let us keep an open mind and let us face the situation in which hypothetically, supposedly, allegedly both parts of the condition are satisfied. Thus, let us imagine a set of numbers whose sum is 100. They must be numbers with one or two figures. There are ten figures, and these ten figures must be all different, since each of the figures, 0, 1, 2, . . . 9 should occur just once. Thus, the sum of all ten figures must be
我们怀疑这种情况实际上不可能出现，而且根据我们不成功的试验的经验，我们的怀疑有一定的依据。然而，让我们保持开放的心态，让我们面对这样的情况：假设，据说，条件的两部分都得到满足。因此，让我们想象一组数字的总和是 100。它们必须是有一个或两个数字的数字。有十个数字，这十个数字必须全部不同，因为每个数字，0，1，2，…… 9 应该只出现一次。因此，所有十个数字的总和必须是
Some of these figures denote units and others tens. It takes a little sagacity to hit upon the idea that the sum of the figures denoting tens may be of some importance. In fact, let t stand for this sum. Then the sum of the remaining figures, denoting units, is 45 − t. Therefore, the sum of all numbers in the set must be
这些数字中有些表示单位，有些表示十。需要一点智慧才能想到，表示十的数字之和可能有一定的重要性。事实上，让t代表这个总和。那么其余表示单位的数字之和为 45-t。
We have here an equation to determine t. It is of the first degree and gives
我们在这里有一个确定t的方程，它是一度的，并给出了
Now, there is something that is definitely wrong. The value of t that we have found is not an integer and t should be, of course, an integer. Starting from the supposition that both parts of the proposed condition can be simultaneously satisfied, we have been led to a manifest absurdity. How can we explain this? Our original supposition must be wrong; both parts of the condition cannot be satisfied at the same time. And so we have attained our goal, we have succeeded in proving that the two parts of the proposed condition are incompatible.
Our reasoning is a typical “reductio ad absurdum.”
我们的推理是一个典型的 “归谬法”。
2. Remarks. Let us look back at the foregoing reasoning and understand its general trend.
2.备注。让我们回顾一下前面的推理，了解其总体趋势。
We wish to prove that it is impossible to fulfill a certain condition, that is, that the situation in which all parts of the condition are simultaneously satisfied can never arise. But, if we have proved nothing yet, we have to face the possibility that the situation could arise. Only by facing squarely the hypothetical situation and examining it closely can we hope to perceive some definitely wrong point in it. And we must lay our hand upon some definitely wrong point if we wish to show conclusively that the situation is impossible. Hence we can see that the procedure that was successful in our example is reasonable in general: We have to examine the hypothetical situation in which all parts of the condition are satisfied, although such a situation appears extremely unlikely.
我们希望证明不可能满足某个条件，也就是说，条件的所有部分同时得到满足的情况不可能出现。但是，如果我们还没有证明什么，我们就必须面对这种情况可能出现的可能性。只有正视假设的情况并仔细研究它，我们才有希望察觉到其中某些绝对错误的地方。如果我们想最终证明这种情况是不可能的，我们就必须把我们的手放在一些绝对错误的地方。因此，我们可以看到，在我们的例子中成功的程序在一般情况下是合理的。我们必须研究条件的所有部分都得到满足的假设情况，尽管这种情况看起来极不可能。
The more experienced reader may see here another point. The main step of our procedure consisted in setting up an equation for t. Now, we could have arrived at the same equation without suspecting that something was wrong with the condition. If we wish to set up an equation, we have to express in mathematical language that all parts of the condition are satisfied, although we do not know yet whether it is actually possible to satisfy all these parts simultaneously.
更有经验的读者可能会在这里看到另一个问题。我们程序的主要步骤包括为t建立一个方程。现在，我们可以在不怀疑条件有问题的情况下得出同一个方程。如果我们想建立一个方程，我们必须用数学语言表达条件的所有部分都得到满足，尽管我们还不知道是否真的有可能同时满足所有这些部分。
Our procedure is “open-minded.” We may hope to find the unknown satisfying the condition, or we may hope to show that the condition cannot be satisfied. It matters little in one respect: the investigation, if it is well conducted, starts in both cases in the same way, examining the hypothetical situation in which the condition is fulfilled, and shows only in its later course which hope is justified.
Compare FIGURES, 2. Compare also PAPPUS; an analysis which ends in disproving the proposed theorem, or in showing that the proposed “problem to find” has no solution, is actually a “reductio ad absurdum.”
比较一下图，2. 再比较一下PAPPUS；一个分析如果以推翻所提出的定理为结束，或者以表明所提出的 “要找的问题” 没有解决办法为结束，实际上就是 “归谬法”。
3. Indirect proof. The prime numbers, or primes, are the numbers 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, . . . which cannot be resolved into smaller factors, although they are greater than 1. (The last clause excludes the number 1 which, obviously, cannot be resolved into smaller factors, but has a different nature and should not be counted as a prime.) The primes are the “ultimate elements” into which all integers (greater than 1) can be decomposed. For instance,
3.间接证明。质数，或称素数，是指 2，3，5，7，11，13，17，19，23，29，31，37，…… 这些数字，尽管它们大于 1，但不能被分解成更小的因子。素数是 “终极元素”，所有整数（大于 1）都可以被分解。比如说。
is decomposed into a product of five primes.
被分解为五个素数的乘积。
Is the series of primes infinite or does it end somewhere? It is natural to suspect that the series of primes never ends. If it ended somewhere, all integers could be decomposed into a finite number of ultimate elements and the world would appear “too poor” in a manner of speaking. Thus arises the problem of proving the existence of an infinity of prime numbers.
素数系列是无限的还是在某处结束？我们很自然地怀疑，素数系列永远不会结束。如果它在某处结束，那么所有的整数都可以被分解成有限的终极元素，那么从某种意义上说，世界将显得 “太穷了”。因此，就出现了证明素数的无穷大存在的问题。
This problem is very different from elementary mathematical problems of the usual kind and appears at first inaccessible. Yet, as we said, it is extremely unlikely that there should be a last prime, say P. Why is it so unlikely?
这个问题与通常的初级数学问题有很大的不同，起初看来是无法解决的。然而，正如我们所说，存在最后一个素数的可能性极小，比如说P，为什么这么小？
Let us face squarely the unlikely situation in which, hypothetically, supposedly, allegedly, there is a last prime P. Then we could write down the complete series of primes 2, 3, 5, 7, 11, . . . P. Why is this so unlikely? What is wrong with it? Can we point out anything that is definitely wrong? Indeed, we can. We can construct the number
This number Q is greater than P and therefore, allegedly, Q cannot be a prime. Consequently, Q must be divisible by a prime. Now, all primes at our disposal are, supposedly, the numbers 2, 3, 5, . . . P but Q, divided by any of these numbers, leaves the rest 1; and so Q is not divisible by any of the primes mentioned which are, hypothetically, all the primes. Now, there is something that is definitely wrong; Q must be either a prime or it must be divisible by some prime. Starting from the supposition that there is a last prime P we have been led to a manifest absurdity. How can we explain this? Our original supposition must be wrong; there cannot be a last prime P. And so we have succeeded in proving that the series of prime numbers never ends.
这个数字Q大于P，因此，据称Q不可能是一个素数。因此，Q必须能被一个素数所除。现在，我们所掌握的所有质数据说是 2、3、5、…… 这些数字。但Q除以这些数字中的任何一个，剩下的都是 1；因此，Q不能被上述任何一个质数整除，而这些质数在假设中是所有的质数。现在，有一些事情肯定是错误的；Q必须是一个素数，或者它必须能被某个素数所除。从存在最后一个素数P的假设出发，我们被引向了一个明显的荒谬。我们如何解释这一点呢？我们最初的假设一定是错的；不可能有最后一个素数P。因此，我们成功地证明了素数系列永远不会结束。
Our proof is a typical indirect proof. (It is a famous proof too, due to Euclid; see Proposition 20 of Book IX of the Elements.)
我们的证明是一个典型的间接证明。（这也是一个著名的证明，归功于欧几里德；见《元素》第九册的命题 20）。
We have established our theorem (that the series of primes never ends) by disproving its contradictory opposite (that the series of primes ends somewhere) which we have disproved by deducing from it a manifest absurdity. Thus we have combined indirect proof with “reductio ad absurdum”; this combination is also very typical.
我们通过反驳其矛盾的反面（质数系列在某处结束）来建立我们的定理（质数系列永不结束），我们通过推导出一个明显的荒谬来反驳它。因此，我们将间接证明与 “归谬法” 结合起来；这种结合也是非常典型的。
4. Objections. The procedures which we are studying encountered considerable opposition. Many objections have been raised which are, possibly, only various forms of the same fundamental objection. We discuss here a “practical” form of the objection, which is on our level.
4.反对意见。我们正在研究的程序遇到了相当多的反对意见。人们提出了许多反对意见，这些反对意见可能只是同一基本反对意见的不同形式。我们在此讨论反对意见的 “实际” 形式，这与我们的水平有关。
To find a not obvious proof is a considerable intellectual achievement but to learn such a proof, or even to understand it thoroughly costs also a certain amount of mental effort. Naturally enough, we wish to retain some benefit from our effort, and, of course, what we retain in our memory should be true and correct and not false or absurd.
But it seems difficult to retain something true from a “reductio ad absurdum.” The procedure starts from a false assumption and derives from it consequences which are equally, but perhaps more visibly, false till it reaches a last consequence which is manifestly false. If we do not wish to store falsehoods in our memory we should forget everything as quickly as possible which is, however, not feasible because all points must be remembered sharply and correctly during our study of the proof.
但似乎很难从 “归谬法” 中保留真实的东西。这个过程从一个错误的假设开始，并从它衍生出同样是错误的，但也许是更明显的错误的后果，直到它达到最后一个明显是错误的后果。如果我们不希望在我们的记忆中储存错误，我们应该尽快忘记一切，但这是不可行的，因为在我们研究证明的过程中，所有的要点都必须被清晰和正确地记住。
The objection to indirect proofs can be now stated very briefly. Listening to such a proof, we are obliged to focus our attention all the time upon a false assumption which we should forget and not upon the true theorem which we should retain.
现在可以非常简要地说明对间接证明的反对意见。听了这样的证明，我们不得不把注意力一直集中在一个我们应该忘记的错误假设上，而不是在我们应该保留的真实定理上。
If we wish to judge correctly of the merits of these objections, we should distinguish between two uses of the “reductio ad absurdum,” as a tool of research and as a means of exposition, and make the same distinction concerning the indirect proof.
如果我们想正确判断这些反对意见的优劣，我们应该区分 “归谬法” 的两种用途，即作为研究的工具和作为论述的手段，并对间接证明作出同样的区分。
It must be confessed that “reductio ad absurdum” as a means of exposition is not an unmixed blessing. Such a “reductio,” especially if it is long, may become very painful indeed for the reader or listener. All the derivations which we examine in succession are correct but all the situations which we have to face are impossible. Even the verbal expression may become tedious if it insists, as it should, on emphasizing that everything is based on an initial assumption; the words “hypothetically,” “supposedly,” “allegedly” must recur incessantly, or some other device must be applied continually. We wish to reject and forget the situation as impossible but we have to retain and examine it as the basis for the next step, and this inner discord may become unbearable in the long run.
Yet it would be foolish to repudiate “reductio ad absurdum” as a tool of discovery. It may present itself naturally and bring a decision when all other means seem to be exhausted as the foregoing examples may show.
然而，否定 “归谬法” 作为一种发现的工具是愚蠢的。当所有其他手段似乎都已用尽时，它可能会自然而然地出现并带来决定，正如前面的例子所显示的那样。
We need some experience to perceive that there is no essential opposition between our two contentions. Experience shows that usually there is little difficulty in converting an indirect proof into a direct proof, or in rearranging a proof found by a long “reductio ad absurdum” into a more pleasant form from which the “reductio ad absurdum” may even completely disappear (or, after due preparation, it may be compressed into a few striking sentences).
我们需要一些经验来认识到，我们的两个论点之间没有本质的对立。经验表明，通常情况下，将一个间接证明转化为直接证明并不困难，或者将一个通过长篇大论的 “归谬法” 找到的证明重新排列成一个更令人愉快的形式，“归谬法” 甚至可以完全消失（或者，经过适当的准备，它可以被压缩成几个引人注目的句子）。
In short, if we wish to make full use of our capacities, we should be familiar both with “reductio ad absurdum” and with indirect proof. When, however, we have succeeded in deriving a result by either of these methods we should not fail to look back at the solution and ask: Can you derive the result differently?
简而言之，如果我们想充分利用我们的能力，我们应该熟悉 “归谬法” 和间接证明。然而，当我们通过这些方法中的任何一种成功地推导出一个结果时，我们不应该不回头看一下解决方案，并问：你能以不同的方式推导出这个结果吗？
Let us illustrate by examples what we have said.
让我们用例子来说明我们所说的内容。
5. Rearranging a reductio ad absurdum. We look back at the reasoning presented under 1. The reductio ad absurdum started from a situation which, eventually, turned out to be impossible. Let us however carve out a part of the argument which is independent of the initial false assumption and contains positive information. Reconsidering what we have done, we may perceive that this much is doubtless true: If a set of numbers with one or two digits is written so that each of the ten figures occurs just once, then the sum of the set is of the form
Thus, this sum is divisible by 9. The proposed puzzle demands however that this sum should be 100. Is this possible? No, it is not, since 100 is not divisible by 9.
因此，这个数字是可以被 9 整除的。然而，拟议的谜题要求这个数字应该是 100。这可能吗？不，不可能，因为 100 不能被 9 整除。
The “reductio ad absurdum” which led to the discovery of the argument vanished from our new presentation.
导致发现该论点的 “归谬法” 在我们的新表述中消失了。
By the way, a reader acquainted with the procedure of “casting out nines” can see now the whole argument at a glance.
顺便说一下，熟悉 “投出 9” 程序的读者现在可以一目了然地看到整个论点。
6. Converting an indirect proof. We look back at the reasoning presented under 3. Reconsidering carefully what we have done, we may find elements of the argument which are independent of any false assumption, yet the best clue comes from a reconsideration of the meaning of the original problem itself.
6.转换一个间接证明。我们回过头来看一下第 3 条下提出的推理。仔细地重新考虑我们所做的，我们可能会发现独立于任何错误假设的论证要素，然而最好的线索来自于对原始问题本身的意义的重新考虑。
What do we mean by saying that the series of primes never ends? Evidently, just this: when we have ascertained any finite set of primes as 2, 3, 5, 7, 11, . . . P, where P is the last prime hitherto found, there is always one more prime. Thus, what must we do to prove the existence of an infinity of primes? We have to point out a way of finding a prime different from all primes hitherto found. Thus, our “problem to prove” is in fact reduced to a “problem to find”: Being given the primes 2, 3, 5, . . . P, find a new prime N different from all the given primes.
我们说素数系列永不结束是什么意思？显然，就是这个意思：当我们确定任何一个有限的素数集为 2，3，5，7，11，…… P，其中P是迄今为止发现的最后一个素数，总有一个更多的素数。因此，我们必须做什么来证明无穷大素数的存在？我们必须指出找到一个与迄今为止发现的所有素数不同的素数的方法。因此，我们的 “证明问题” 实际上被简化为一个 “寻找问题”。给出素数2，3，5，…… P，找到一个与所有给定素数不同的新素数 N。
Having restated our original problem in this new form, we have taken the main step. It is relatively easy now to see how to use the essential parts of our former argument for the new purpose. In fact, the number
在以这种新的形式重述了我们原来的问题之后，我们已经迈出了主要的一步。现在可以比较容易地看到如何将我们以前论证的基本部分用于新的目的。事实上，这个数字
is certainly divisible by a prime. Let us take—this is the idea—any prime divisor of Q (for instance, the smallest one) for N. (Of course, if Q happens to be a prime, then N = Q.) Obviously, Q divided by any of the primes 2, 3, 5, . . . P leaves the remainder 1 and, therefore, none of these numbers can be N which is a divisor of Q. But that is all we need: N is a prime, and different from all hitherto found primes 2, 3, 5, 7, 11, . . . P.
This proof gives a definite procedure of prolonging again and again the series of primes, without limit. Nothing is indirect in it, no impossible situation needs to be considered. Yet, fundamentally, it is the same as our former indirect proof which we have succeeded in converting.
这个证明给出了一个明确的程序，可以一次又一次地延长素数系列，没有限制。这里面没有任何间接的东西，没有任何不可能的情况需要考虑。然而，从根本上说，它与我们以前的间接证明是一样的，我们已经成功地转换了。
Routine problem may be called the problem to solve the equation x2 − 3x + 2 = 0 if the solution of the general quadratic equation was explained and illustrated before so that the student has nothing to do but to substitute the numbers −3 and 2 for certain letters which appear in the general solution. Even if the quadratic equation was not solved generally in “letters” but half a dozen similar quadratic equations with numerical coefficients were solved just before, the problem should be called a “routine problem.” In general, a problem is a “routine problem” if it can be solved either by substituting special data into a formerly solved general problem, or by following step by step, without any trace of originality, some well-worn conspicuous example. Setting a routine problem, the teacher thrusts under the nose of the student an immediate and decisive answer to the question: Do you know a related problem? Thus, the student needs nothing but a little care and patience in following a cut-and-dried precept, and he has no opportunity to use his judgment or his inventive faculties.
常规问题可以称为解方程x2-3x+2=0 的问题，如果一般的二次方程的解法在之前已经被解释和说明过了，所以学生除了用数字-3 和 2 代替一般解法中出现的某些字母外，什么都不用做。即使这个一元二次方程没有用 “字母” 进行一般的解法，但之前有半打类似的带数字系数的一元二次方程被解决了，这个问题也应该被称为 “常规问题”。一般来说，如果一个问题可以通过将特殊数据替换到以前解决的一般问题中来解决，或者通过按部就班、没有任何原创性地遵循一些老掉牙的明显例子来解决，那么它就是一个 “常规问题”。设置一个常规问题，教师在学生眼皮底下推送一个直接的、决定性的问题答案。你知道一个相关的问题吗？这样一来，学生只需要小心和耐心地遵循一条干巴巴的规则，而没有机会使用他的判断力或创造性。
Routine problems, even many routine problems, may be necessary in teaching mathematics but to make the students do no other kind is inexcusable. Teaching the mechanical performance of routine mathematical operations and nothing else is well under the level of the cookbook because kitchen recipes do leave something to the imagination and judgment of the cook but mathematical recipes do not.
It may be good to be reminded somewhat rudely that certain aspirations are hopeless. Infallible rules of discovery leading to the solution of all possible mathematical problems would be more desirable than the philosophers’ stone, vainly sought by the alchemists. Such rules would work magic; but there is no such thing as magic. To find unfailing rules applicable to all sorts of problems is an old philosophical dream; but this dream will never be more than a dream.
有些人粗暴地提醒我们，某些愿望是没有希望的，这也许是好事。导致解决所有可能的数学问题的无懈可击的发现规则将比炼金术士徒劳地寻找的哲学家之石更令人向往。这样的规则会产生魔力；但没有魔力这回事。找到适用于各种问题的不折不扣的规则是一个古老的哲学梦想；但这个梦想永远不会只是一个梦想。
A reasonable sort of heuristic cannot aim at unfailing rules; but it may endeavor to study procedures (mental operations, moves, steps) which are typically useful in solving problems. Such procedures are practiced by every sane person sufficiently interested in his problem. They are hinted by certain stereotyped questions and suggestions which intelligent people put to themselves and intelligent teachers to their students. A collection of such questions and suggestions, stated with sufficient generality and neatly ordered, may be less desirable than the philosophers’ stone but can be provided. The list we study provides such a collection.
合理的启发式不能以无懈可击的规则为目标；但它可以努力研究在解决问题时通常有用的程序（心理操作、动作、步骤）。每一个对自己的问题有足够兴趣的理智的人都会采用这样的程序。聪明人对自己和聪明的老师对学生提出的某些定型的问题和建议都暗示了这些程序。这种问题和建议的集合，以足够的概括性和整齐的顺序，可能比哲学家的石头更不可取，但可以提供。我们研究的清单就提供了这样一个集合。
First things come first. The author of this book does not think that all rules of conduct for teachers are completely useless; otherwise, he would not have dared to write a whole book about the conduct of teachers and students. Yet it should not be forgotten that a teacher of mathematics should know some mathematics, and that a teacher wishing to impart the right attitude of mind toward problems to his students should have acquired that attitude himself.
首先要做的是。本书作者并不认为所有的教师行为准则都是完全无用的；否则，他就不敢写一整本关于教师和学生行为的书。然而，我们不应忘记，一个数学教师应该懂得一些数学知识，而一个希望向学生传授对问题的正确态度的教师，自己也应该掌握这种态度。
Separate the various parts of the condition. Our first duty is to understand the problem. Having understood the problem as a whole, we go into detail. We consider its principal parts, the unknown, the data, the condition, each by itself. When we have these parts well in mind but no particularly helpful idea has yet occurred to us, we go into further detail. We consider the various data, each datum by itself. Having understood the condition as a whole, we separate its various parts, and we consider each part by itself.
We see now the role of the suggestion that we have to discuss here. It tends to provoke a step that we have to take when we are trying to see the problem distinctly and have to go into finer and finer detail. It is a step in DECOMPOSING AND RECOMBINING.
我们现在看到了我们在这里必须讨论的建议的作用。它倾向于引发一个步骤，当我们试图清楚地看到问题，并不得不进入越来越细的细节时，我们必须采取这个步骤。这是解构和重组的一个步骤。
Separate the various parts of the condition. Can you write them down? We often have opportunity to ask this question when we are SETTING UP EQUATIONS.
把条件的各个部分分开。你能把它们写下来吗？我们在设置方程时经常有机会问这个问题。
1. To set up equations means to express in mathematical symbols a condition that is stated in words; it is translation from ordinary language into the language of mathematical formulas. The difficulties which we may have in setting up equations are difficulties of translation.
1. 建立方程意味着用数学符号表达一个用文字表述的条件；它是从普通语言翻译成数学公式的语言。我们在建立方程时可能遇到的困难是翻译的困难。
In order to translate a sentence from English into French two things are necessary. First, we must understand thoroughly the English sentence. Second, we must be familiar with the forms of expression peculiar to the French language. The situation is very similar when we attempt to express in mathematical symbols a condition proposed in words. First, we must understand thoroughly the condition. Second, we must be familiar with the forms of mathematical expression.
为了将一个句子从英语翻译成法语，有两件事是必要的。首先，我们必须彻底理解英语句子。第二，我们必须熟悉法语特有的表达形式。当我们试图用数学符号来表达一个用文字提出的条件时，情况也非常类似。首先，我们必须彻底理解这个条件。其次，我们必须熟悉数学表达的形式。
An English sentence is relatively easy to translate into French if it can be translated word for word. But there are English idioms which cannot be translated into French word for word. If our sentence contains such idioms, the translation becomes difficult; we have to pay less attention to the separate words, and more attention to the whole meaning; before translating the sentence, we may have to rearrange it.
如果一个英语句子可以逐字翻译成法语，那么翻译起来相对容易。但有些英语习语是不能逐字翻译成法语的。如果我们的句子中含有这样的习语，翻译就会变得很困难；我们必须减少对单独单词的关注，而更多地关注整个意思；在翻译句子之前，我们可能必须重新安排它。
It is very much the same in setting up equations. In easy cases, the verbal statement splits almost automatically into successive parts, each of which can be immediately written down in mathematical symbols. In more difficult cases, the condition has parts which cannot be immediately translated into mathematical symbols. If this is so, we must pay less attention to the verbal statement, and concentrate more upon the meaning. Before we start writing formulas, we may have to rearrange the condition, and we should keep an eye on the resources of mathematical notation while doing so.
In all cases, easy or difficult, we have to understand the condition, to separate the various parts of the condition, and to ask: Can you write them down? In easy cases, we succeed without hesitation in dividing the condition into parts that can be written down in mathematical symbols; in difficult cases, the appropriate division of the condition is less obvious.
在所有情况下，不管是容易还是困难，我们都必须理解条件，把条件的各个部分分开，并问：你能把它们写下来吗？在容易的情况下，我们可以毫不犹豫地将条件划分为可以用数学符号写下来的部分；在困难的情况下，条件的适当划分就不那么明显了。
The foregoing explanation should be read again after the study of the following examples.
前面的解释应该在学习了下面的例子之后再读。
2. Find two quantities whose sum is 78 and whose product is 1296.
2.找出两个和为78、积为1296 的量。
We divide the page by a vertical line. On one side, we write the verbal statement split into appropriate parts. On the other side, we write algebraic signs, opposite to the corresponding part of the verbal statement. The original is on the left, the translation into symbols on the right.
我们用一条垂直线来划分这一页。在一边，我们写下被分成适当部分的口头陈述。在另一边，我们写上代数符号，与口头陈述的相应部分相对。原文在左边，翻译成符号在右边。
In this case, the verbal statement splits almost automatically into successive parts, each of which can be immediately written down in mathematical symbols.
在这种情况下，口头陈述几乎自动分割成连续的部分，每一部分都可以立即用数学符号写下来。
3. Find the breadth and the height of a right prism with square base, being given the volume, 63 cu. in., and the area of the surface, 102 sq. in.
3.给定体积为 63立方英寸，表面面积为 102平方英寸，求一个方底的直角棱柱的宽和高。
What are the unknowns? The side of the base, say x, and the altitude of the prism, say y.
未知数是什么？底座的边，例如x，和棱镜的高度，例如y。
What is the condition? The prism whose base is a square with side x and whose altitude is y must have the volume 63 and the area 102.
条件是什么？底部是边长为x的正方形，高度为y的棱柱，其体积必须是 63，面积是 102。
Separate the various parts of the condition. There are two parts, one concerned with the volume, the other with the area.
把条件的各个部分分开。有两个部分，一个是关于体积的，另一个是关于面积的。
We can scarcely hesitate in dividing the whole condition just in these two parts; but we cannot write down these parts “immediately.” We must know how to calculate the volume and the various parts of the area. Yet, if we know that much geometry, we can easily restate both parts of the condition so that the translation into equations is feasible. We write on the left hand side of the page an essentially rearranged and expanded statement of the problem, ready for translation into algebraic language.
我们几乎可以毫不犹豫地将整个条件仅仅划分为这两部分；但我们不能 “立即” 写下这些部分。我们必须知道如何计算体积和面积的各个部分。然而，如果我们知道这么多的几何学知识，我们就可以很容易地重述条件的两部分，以便转化为方程是可行的。我们在页面的左侧写下一个基本上经过重新排列和扩展的问题陈述，准备转化为代数语言。
This is a problem of plane analytic geometry.
这是一个平面解析几何的问题。
What is the unknown? A point, with coordinates, say, p, q.
未知数是什么？一个点，其坐标为p，q。
What is given? The equation of a straight line, say y = mx + n, and a point with coordinates, say, a, b.
给出的是什么？直线的方程，如y=mx+n，和一个点的坐标，如a，b。
What is the condition? The points (a, b) and (p, q) are symmetrical to each other with respect to the line y = mx + n.
该条件是什么？点（a，b）和（p，q）相对于直线y=mx+n是相互对称的。
We now reach the essential difficulty which is to divide the condition into parts each of which can be expressed in the language of analytic geometry. The nature of this difficulty must be well understood. A decomposition of the condition into parts may be logically unobjectionable and nevertheless useless. What we need here is a decomposition into parts which are fit for analytic expression. In order to find such a decomposition we must go back to the definition of symmetry, but keep an eye on the resources of analytic geometry. What is meant by symmetry with respect to a straight line? What geometric relations can we express simply in analytic geometry? We concentrate upon the first question, but we should not forget the second. Thus, eventually, we may find the decomposition which we are going to state.
我们现在达到了基本的困难，即把条件分成几个部分，每个部分都可以用解析几何的语言来表达。必须很好地理解这一困难的性质。将条件分解成若干部分可能在逻辑上没有异议，但却没有用。我们在这里需要的是分解成适合分析表达的部分。为了找到这样的分解，我们必须回到对称性的定义中去，但要注意分析几何的资源。相对于直线的对称性是什么意思？我们可以在解析几何中简单地表达哪些几何关系？我们专注于第一个问题，但我们不应该忘记第二个问题。因此，最终，我们可能会找到我们将要陈述的分解。
Signs of progress. As Columbus and his companions sailed westward across an unknown ocean they were cheered whenever they saw birds. They regarded a bird as a favorable sign, indicating the nearness of land. But in this they were repeatedly disappointed. They watched for other signs too. They thought that floating seaweed or low banks of cloud might indicate land, but they were again disappointed. One day, however, the signs multiplied. On Thursday, the 11th of October, 1492, “they saw sandpipers, and a green reed near the ship. Those of the caravel Pinta saw a cane and a pole, and they took up another small pole which appeared to have been worked by iron; also another bit of cane, a land-plant, and a small board. The crew of the caravel Niña also saw signs of land, and a small branch covered with berries. Everyone breathed afresh and rejoiced at these signs.” And in fact the next day they sighted land, the first island of a New World.
进步的标志。当哥伦布和他的同伴们在未知的海洋中向西航行时，每当他们看到鸟类就会感到高兴。他们认为鸟是一个有利的信号，表明离陆地不远了。但在这一点上，他们屡屡感到失望。他们也在观察其他迹象。他们认为漂浮的海草或低矮的云层可能表明有陆地，但他们再次感到失望。然而，有一天，这些迹象成倍增加。1492 年 10 月 11 日，星期四，“他们看到了鹬蚌相争，船边有一根绿色的芦苇。平塔号船上的人看到了一根甘蔗和一根竹竿，他们又拿起了一根小竹竿，这根竹竿似乎是用铁做的；还看到了另一根甘蔗、一株植物和一块小板。尼娜号船的船员也看到了土地的迹象，还有一根长满浆果的小树枝。每个人都因这些迹象而重新呼吸，并感到高兴”。事实上，第二天他们就看到了陆地，一个新世界的第一个岛屿。
Our undertaking may be important or unimportant, our problem of any kind—when we are working intensely, we watch eagerly for signs of progress as Columbus and his companions watched for signs of approaching land. We shall discuss a few examples in order to understand what can be reasonably regarded as a sign of approaching the solution.
我们的事业可能是重要的或不重要的，我们的问题可能是任何种类的 —— 当我们正在紧张地工作时，我们急切地观察进展的迹象，就像哥伦布和他的同伴们观察接近陆地的迹象一样。我们将讨论几个例子，以了解什么可以合理地被视为接近解决方案的迹象。
1. Examples. I have a chess problem. I have to mate the black king in, say, two moves. On the chessboard there is a white knight, quite a distance from the black king, that is apparently superfluous. What is it good for? I am obliged to leave this question unanswered at first. Yet after various trials, I hit upon a new move and observe that it would bring that apparently superfluous white knight into play. This observation gives me a new hope. I regard it as a favorable sign: that new move has some chance to be the right one. Why?
1.例子。我有一个国际象棋问题。我必须在比如说两步内配上黑王。棋盘上有一个白马，离黑王有一段距离，显然是多余的。它有什么用呢？我不得不一开始就不回答这个问题。然而经过各种试验之后，我发现了一个新的棋步，并观察到它会使那个明显多余的白马发挥作用。这一观察给了我一个新的希望。我认为这是一个有利的信号：这步新棋有可能是正确的。为什么呢？
In a well-constructed chess problem there is no superfluous piece. Therefore, we have to take into account all chessmen on the board; we have to use all the data. The correct solution does certainly use all the pieces, even that apparently superfluous white knight. In this last respect, the new move that I contemplate agrees with the correct move that I am supposed to find. The new move looks like the correct move; it might be the correct move.
It is interesting to consider a similar situation in a mathematical problem. My task is to express the area of a triangle in terms of its three sides, a, b, and c. I have already made some sort of plan. I know, more or less clearly, which geometrical connections I have to take into account and what sort of calculations I have to perform. Yet I am not quite sure whether my plan will work. If now, proceeding along the line prescribed by my plan, I observe that the quantity
考虑一个数学问题中的类似情况是很有意思的。我的任务是用一个三角形的三条边a、b、c来表示它的面积，我已经制定了某种计划。我或多或少知道我必须考虑哪些几何关系，必须进行什么样的计算。但我不太确定我的计划是否会成功。如果现在，沿着我的计划规定的路线前进，我观察到数量
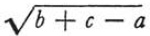
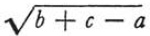
enters into the expression of the area I am about to construct, I have good reason to be cheered. Why?
进入我即将建设的地区的表达，我有充分的理由感到欢欣鼓舞。为什么？
In fact, it must be taken into account that the sum of any two sides of a triangle is greater than the third side. This involves a certain restriction. The given lengths, a, b, and c cannot be quite arbitrary; for instance, b + c must be greater than a. This is an essential part of the condition, and we should use the whole condition. If b + c is not greater than a the formula I seek is bound to become illusory. Now, the square root displayed above becomes imaginary if b + c − a is negative—that is, if b + c is less than a—and so the square root becomes unfit to represent a real quantity under just those circumstances under which the desired expression is bound to become illusory. Thus my formula, into which that square root enters, has an important property in common with the true formula for the area. My formula looks like the true formula; it might be the true formula.
Here is one more example. Some time ago, I wished to prove a theorem in solid geometry. Without much trouble I found a first remark that appeared to be pertinent; but then I got stuck. Something was missing to finish the proof. When I gave up that day I had a much clearer notion than at the outset how the proof should look, how the gap should be filled; but I was not able to fill it. The next day, after a good night’s rest, I looked again into the question and soon hit upon an analogous theorem in plane geometry. In a flash I was convinced that now I had got hold of the solution and I had, I think, good reason too to be convinced. Why?
这里还有一个例子。前段时间，我想证明一个实体几何学的定理。我不费吹灰之力就找到了第一条似乎是相关的评论；但后来我被卡住了。在完成证明的过程中还缺少一些东西。当我那天放弃的时候，我有了一个比一开始更清楚的概念，证明应该是怎样的，这个缺口应该怎样填补；但我无法填补它。第二天，经过一夜的休息，我再次研究这个问题，并很快在平面几何中找到了一个类似的定理。一瞬间，我确信现在我已经掌握了解决方案，而且我想，我也有充分的理由确信这一点。为什么呢？
In fact, analogy is a great guide. The solution of a problem in solid geometry often depends on an analogous problem in plane geometry (see ANALOGY, 3-7). Thus, in my case, there was a chance from the outset that the desired proof would use as a lemma some theorem of plane geometry of the kind which actually came to my mind. “This theorem looks like the lemma I need; it might be the lemma I need”—such was my reasoning.
事实上，类比是一个很好的指导。实体几何中一个问题的解决往往取决于平面几何中一个类似的问题（见 “类比”，3-7）。因此，在我的例子中，从一开始就有机会，所需的证明将使用平面几何中的某个定理，作为我脑海中实际出现的那种定理。“这个定理看起来像我需要的定理；它可能是我需要的定理” —— 这就是我的推理。
If Columbus and his men had taken the trouble to reason explicitly, they would have reasoned in some similar way. They knew how the sea looks near the shore. They knew that, more often than on the open sea, there are birds in the air, coming from the land, and objects floating in the water, detached from the seashore. Many of the men must have observed such things when from former voyages they had returned to their home port. The day before that memorable date on which they sighted the island of San Salvador, as the floating objects in the water became so frequent, they thought: “It looks as if we were approaching some land; we may be approaching some land” and “everyone breathed afresh and rejoiced at these signs.”
2. Heuristic character of signs of progress. Let us insist upon a point which is perhaps already clear to everyone; but it is very important and, therefore, it should be completely clear.
2.进展迹象的启发式特点。让我们坚持一个也许大家都已经很清楚的观点；但它非常重要，因此，应该完全清楚。
The type of reasoning illustrated by the foregoing examples deserves to be noticed and taken into account seriously, although it yields only a plausible indication and not an unfailing certainty. Let us restate pedantically, at full length, in rather unnatural detail, one of these reasonings:
上述例子所说明的推理类型值得注意和认真考虑，尽管它只产生了一个可信的迹象，而不是一个不折不扣的确定性。让我们用相当不自然的细节，完整地重述这些推理中的一个。
If we are approaching land, we often see birds.
如果我们正在接近陆地，我们经常会看到鸟类。
Now we see birds.
现在我们看到了鸟。
Therefore, probably, we are approaching land.
因此，可能，我们正在接近陆地。
Without the word “probably” the conclusion would be an outright fallacy. In fact, Columbus and his companions saw birds many times but were disappointed later. Just once came the day on which they saw sandpipers followed by the day of discovery.
如果没有 “可能” 一词，这个结论将是一个彻头彻尾的谬论。事实上，哥伦布和他的同伴们多次看到鸟类，但后来都感到失望。只是有一次，他们看到了鹬蚌相争的那一天，紧接着就是发现的那一天。
With the word “probably” the conclusion is reasonable and natural but by no means a proof, a demonstrative conclusion; it is only an indication, a heuristic suggestion. It would be a great mistake to forget that such a conclusion is only probable, and to regard it as certain. But to disregard such conclusions entirely would be a still greater mistake. If you take a heuristic conclusion as certain, you may be fooled and disappointed; but if you neglect heuristic conclusions altogether you will make no progress at all. The most important signs of progress are heuristic. Should we trust them? Should we follow them? Follow, but keep your eyes open. Trust but look. And never renounce your judgment.
用 “大概” 这个词，结论是合理的、自然的，但决不是一个证明，一个示范性的结论；它只是一个指示，一个启发式的建议。如果忘记这样的结论只是可能的，而把它视为肯定的，那将是一个很大的错误。但是，完全无视这样的结论将是一个更大的错误。如果你把启发式的结论当作是确定的，你可能会被愚弄和失望；但如果你完全忽视启发式的结论，你将完全没有进展。进步的最重要标志是启发式的。我们应该相信它们吗？我们应该跟随他们吗？跟随，但要睁大你的眼睛。相信但要看。而且永远不要放弃你的判断。
In one of these examples, we regarded as a favorable sign that we succeeded in bringing into play a datum not used before (the white knight). We were quite right to so regard it. In fact, to solve a problem is, essentially, to find the connection between the data and the unknown. Moreover we should, at least in well-stated problems, use all the data, connect each of them with the unknown. Thus, bringing one more datum into play is quite properly felt as progress, as a step forward.
在其中一个例子中，我们认为这是一个有利的迹象，即我们成功地发挥了一个以前没有使用过的数据（白马）。我们这样看待它是非常正确的。事实上，要解决一个问题，从本质上讲，就是要找到数据和未知事物之间的联系。此外，至少在陈述清楚的问题中，我们应该使用所有的数据，将它们中的每一个与未知数联系起来。因此，多用一个数据就会被认为是进步，是向前迈出的一步。
In another example, we regarded as a favorable sign that an essential clause of the condition was appropriately taken into account by our formula. We were quite right to so regard it. In fact, we should use the whole condition. Thus, taking into account one more clause of the condition is justly felt as progress, as a move in the right direction.
在另一个例子中，我们认为这是一个有利的迹象，即我们的公式适当地考虑到了条件的一个基本条款。我们这样看待它是非常正确的。事实上，我们应该使用整个条件。因此，考虑到条件中的另一个条款，我们有理由认为是一种进步，是朝着正确的方向前进。
In still another example, we regarded as a favorable sign the emergence of a simpler analogous problem. This also is justified. Indeed, analogy is one of the main sources of invention. If other means fail, we should try to imagine an analogous problem. Therefore, if such a problem emerges spontaneously, by its own accord, we naturally feel elated; we feel that we are approaching the solution.
在另一个例子中，我们把一个更简单的类似问题的出现视为一个有利的信号。这也是有道理的。事实上，类比是发明的主要来源之一。如果其他方法失败了，我们应该尝试想象一个类似的问题。因此，如果这样的问题自发地出现了，我们自然会感到高兴；我们觉得我们正在接近解决方案。
After these examples, we can now easily grasp the general idea. There are certain mental operations typically useful in solving problems. (The most usual operations of this kind are listed in this book.) If such a typical operation succeeds (if one more datum is connected with the unknown—one more clause of the condition is taken into account—a simpler analogous problem is introduced) its success is felt as a sign of progress. Having understood this essential point, we can express with some clearness the nature of still other signs of progress. All we have to do is to read down our list and look at the various questions and suggestions from our newly acquired point of view.
Thus, understanding clearly the nature of the unknown means progress. Clearly disposing the various data so that we can easily recall any one also means progress. Visualizing vividly the condition as a whole may mean an essential advance; and separating the condition into appropriate parts may be an important step forward. When we have found a figure that we can easily imagine, or a notation that we can easily retain, we can reasonably believe that we have made some progress. Recalling a problem related to ours and solved before may be a decisive move in the right direction.
因此，清楚地了解未知事物的性质意味着进步。清楚地处理各种数据，使我们能够轻松地回忆起任何一个数据，也意味着进步。将条件作为一个整体生动地展示出来，可能意味着一个重要的进步；而将条件分成适当的部分，可能是一个重要的进步。当我们找到一个我们可以轻松想象的数字，或者一个我们可以轻松保留的符号时，我们就可以合理地认为我们已经取得了一些进展。回顾一个与我们有关的、以前解决过的问题，可能是朝着正确方向迈出的决定性一步。
And so on, and so forth. To each mental operation clearly conceived corresponds a certain sign clearly expressible. Our list, appropriately read, lists also signs of progress.
以此类推。每一个被明确设想的心理操作都对应着一个可以明确表达的特定标志。我们的清单，适当地阅读，也列出了进步的标志。
Now, the questions and suggestions of our list are simple, obvious, just plain common sense. This has been said repeatedly and the same can be said of the connected signs of progress we discuss here. To read such signs no occult science is needed, only a little common sense and, of course, a little experience.
现在，我们清单上的问题和建议是简单、明显的，只是普通的常识。这一点已经被反复说过了，我们在这里讨论的进步的相关迹象也可以这么说。要读懂这些迹象，不需要任何神秘的科学，只需要一点常识，当然还有一点经验。
4. Less clearly expressible signs. When we work intently, we feel keenly the pace of our progress: when it is rapid we are elated; when it is slow we are depressed. We feel such differences quite clearly without being able to point out any distinct sign. Moods, feelings, general aspects of the situation serve to indicate our progress. They are not easy to express. “It looks good to me,” or “It is not so good,” say the unsophisticated. More sophisticated people express themselves with some nuance: “This is a well-balanced plan,” or “No, something is still lacking and that spoils the harmony.” Yet behind primitive or vague expressions there is an unmistakable feeling which we follow with confidence and which leads us frequently in the right direction. If such feeling is very strong and emerges suddenly, we speak of inspiration. People usually cannot doubt their inspirations and are sometimes fooled by them. In fact, we should treat guiding feelings and inspirations just as we treat the more clearly expressible signs of progress which we have considered before. Trust, but keep your eyes open.
4.不太明显的迹象。当我们专心致志地工作时，我们会敏锐地感觉到我们的进展速度：当进展迅速时，我们会感到高兴；当进展缓慢时，我们会感到沮丧。我们很清楚地感受到这种差异，但却无法指出任何明显的迹象。心情、感觉、情况的一般方面有助于表明我们的进展。它们不容易表达。不成熟的人说：“我看起来不错”，或 “不那么好”，。更加老练的人则以一些细微的差别来表达自己。“这是一个很平衡的计划”，或 “不，仍然缺少一些东西，这破坏了和谐。” 然而，在原始或模糊的表达背后，有一种明确无误的感觉，我们满怀信心地追随它，它经常引导我们走向正确的方向。如果这种感觉非常强烈并突然出现，我们就说是灵感。人们通常不能怀疑自己的灵感，有时会被它所迷惑。事实上，我们应该像对待我们之前考虑过的更明确的进步迹象一样，对待指导性的感觉和灵感。相信，但要睁大眼睛。
Always follow your inspiration—with a grain of doubt.
始终追随你的灵感 —— 带着一丝怀疑。
[What is the nature of those guiding feelings? Is there some less vague meaning behind words of such aesthetic nuances as “well-balanced,” or “harmonious”? These questions may be more speculative than practical, but the present context indicates answers which perhaps deserve to be stated: Since the more clearly expressible signs of progress are connected with the success or failure of certain rather definite mental operations, we may suspect that our less clearly expressible guiding feelings may be similarly connected with other, more obscure, mental activities—perhaps with activities whose nature is more “psychological” and less “logical.”]
[这些指导性感受的性质是什么？在 “均衡” 或 “和谐” 这样的美学细微差别的词语背后，是否有一些不太模糊的含义？这些问题可能更多的是推测性的，而不是实用性的，但目前的情况表明，这些答案也许值得被说明。既然更明确的可表达的进步迹象与某些相当明确的心理操作的成功或失败有关，我们可以怀疑，我们不太明确的可表达的指导性感觉可能同样与其他更模糊的心理活动有关 —— 也许与那些性质更 “心理”、更不 “逻辑” 的活动有关。］
5. How signs help. I have a plan. I see pretty clearly where I should begin and which steps I should take first. Yet I do not quite see the lay-out of the road farther on; I am not quite certain that my plan will work; and, in any case, I have still a long way to go. Therefore, I start out cautiously in the direction indicated by my plan and keep a lookout for signs of progress. If the signs are rare or indistinct, I become more hesitant. And if for a long time they fail to appear altogether, I may lose courage, turn back, and try another road. On the other hand, if the signs become more frequent as I proceed, if they multiply, my hesitation fades, my spirits rise, and I move with increasing confidence, just as Columbus and his companions did before sighting the island of San Salvador.
Signs may guide our acts. Their absence may warn us of a blind alley and save us time and useless exertion; their presence may cause us to concentrate our effort upon the right spot.
迹象可以指导我们的行为。它们的缺失可能会提醒我们注意盲道，并为我们节省时间和无用的努力；它们的存在可能会使我们将努力集中在正确的地方。
Yet signs may also be deceptive. I once abandoned a certain path for lack of signs, but a man who came after me and followed that path a little farther made an important discovery—to my great annoyance and long-lasting regret. He not only had more perseverance than I did but he also read correctly a certain sign which I had failed to notice. Again, I may follow a road cheerfully, encouraged by favorable signs, and run against an unsuspected and insurmountable obstacle.
然而，迹象也可能是欺骗性的。有一次，我因为缺乏征兆而放弃了某条路，但一个在我之后沿着那条路走了一段距离的人有了一个重要的发现 —— 这让我非常恼火，并留下了长久的遗憾。他不仅比我更有毅力，而且他还正确地读出了我没有注意到的某个标志。同样，我可能在有利迹象的鼓励下，兴高采烈地沿着一条路走，却遇到了一个未曾预料到的、无法克服的障碍。
Yes, signs may misguide us in any single case, but they guide us right in the majority of them. A hunter may misinterpret now and then the traces of his game but he must be right on the average, otherwise he could not make a living by hunting.
是的，迹象可能在任何单一的情况下误导我们，但它们在大多数情况下都能引导我们正确。一个猎人可能偶尔会误解他的猎物的踪迹，但他必须在平均水平上是正确的，否则他就不能靠打猎为生。
It takes experience to interpret the signs correctly. Some of Columbus’s companions certainly knew by experience how the sea looks near the shore and so they were able to read the signs which suggested that they were approaching land. The expert knows by experience how the situation looks and feels when the solution is near and so he is able to read the signs which indicate that he is approaching it. The expert knows more signs than the inexperienced, and he knows them better; his main advantage may consist in such knowledge. An expert hunter notices traces of game and appraises even their freshness or staleness where the inexperienced one is unable to see anything.
要正确解释这些迹象需要经验。哥伦布的一些同伴通过经验当然知道海岸附近的海面是什么样子的，所以他们能够读懂那些表明他们正在接近陆地的迹象。专家通过经验知道，当解决方案接近时，情况看起来和感觉如何，所以他能够读出表明他正在接近的迹象。专家比没有经验的人知道更多的迹象，而且他更了解这些迹象；他的主要优势可能就在于这种知识。一个专家级的猎人会注意到猎物的踪迹，甚至会评估它们的新鲜度或陈旧度，而没有经验的人却无法看到任何东西。
[6. Heuristic syllogism. In section 2 we came across a mode of heuristic reasoning that deserves further consideration and a technical term. We begin by restating that reasoning in the following form:
[6.启发式论证。在第 2 节中，我们遇到了一种启发式推理的模式，值得进一步考虑并使用一个技术术语。我们首先以如下形式重述这种推理。
If we are approaching land, we often see birds.
如果我们正在接近陆地，我们经常会看到鸟类。
Now we see birds.
现在我们看到了鸟。
Therefore, it becomes more credible that we are approaching land.
因此，我们正在接近陆地的说法变得更加可信。
The two statements above the horizontal line may be called the premises, the statement under the line, the conclusion. And the whole pattern of reasoning may be termed a heuristic syllogism.
横线上面的两个陈述可以称为前提，横线下面的陈述是结论。而整个推理模式可以被称为启发式三段论。
The premises are stated here in the same form as in section 2, but the conclusion is more carefully worded. An essential circumstance is better emphasized. Columbus and his men conjectured from the beginning that they would eventually find land sailing westward; and they must have given some credence to this conjecture, otherwise they would not have started out at all. As they proceeded, they related every incident, major or minor, to their dominating question: “Are we approaching land?” Their confidence rose and fell as events occurred or failed to occur, and each man’s beliefs fluctuated more or less differently according to his background and character. The whole dramatic tension of the voyage is due to such fluctuations of confidence.
这里的前提与第 2 节的形式相同，但结论的措辞更加谨慎。一个基本情况得到了更好的强调。哥伦布和他的手下从一开始就猜想，他们最终会找到向西航行的陆地；而且他们肯定对这一猜想给予了一定的信任，否则他们根本就不会开始行动。在他们前进的过程中，他们把每一个事件，无论大小，都与他们的主导问题联系起来。"我们正在接近陆地吗？他们的信心随着事件的发生或失败而起伏，而每个人的信念也根据他的背景和性格或多或少地发生了变化。整个航程的戏剧性紧张是由于这种信心的波动造成的。
The general pattern suggested by our example can be exhibited thus:
我们的例子所提示的一般模式可以这样展示。
If A is true, then B is also true, as we know.
Now, it turns out that B is true.
如果A是真的，那么B也是真的，正如我们所知。
现在，事实证明，B是真的。
Therefore, A becomes more credible.
因此，A变得更加可信。
Still shorter:
还是比较短。
In this schematic statement the horizontal line stands for the word “therefore” and expresses the implication, the essential link between the premises and the conclusion.]
在这个示意图中，横线代表了 “因此” 一词，表达了暗示，即前提和结论之间的基本联系] 。
[7. Nature of plausible reasoning. In this little book we are discussing a philosophical question. We discuss it as practically and informally and as far from high-brow modes of expression as we can, but nevertheless our subject is philosophical. It is concerned with the nature of heuristic reasoning and, by extension, with a kind of reasoning which is nondemonstrative although important and which we shall call, for lack of a better term, plausible reasoning.
[7. 合理推理的性质。在这本小书中，我们讨论的是一个哲学问题。我们尽可能实际地、非正式地讨论它，尽可能远离高深莫测的表达方式，但尽管如此，我们的主题是哲学性的。它涉及启发式推理的性质，并延伸到一种推理，这种推理虽然很重要，但却不具示范性，由于缺乏更好的术语，我们将把它称为可信的推理。
The signs that convince the inventor that his idea is good, the indications that guide us in our everyday affairs, the circumstantial evidence of the lawyer, the inductive evidence of the scientist, statistical evidence invoked in many and diverse subjects—all these kinds of evidence agree in two essential points. First, they do not have the certainty of a strict demonstration. Second, they are useful in acquiring essentially new knowledge, and even indispensable to any not purely mathematical or logical knowledge, to any knowledge concerned with the physical world. We could call the reasoning that underlies this kind of evidence “heuristic reasoning” or “inductive reasoning” or (if we wish to avoid stretching the meaning of existing terms) “plausible reasoning.” We accept here the last term.
The heuristic syllogism introduced in the foregoing may be regarded as the simplest and most widespread pattern of plausible reasoning. It reminds us of a classical pattern of demonstrative reasoning, of the so-called “modus tollens of hypothetical syllogism.” We exhibit here both patterns side by side:
前面介绍的启发式三段论可以被看作是最简单和最普遍的合理推理模式。它让我们想起了一种经典的证明性推理模式，即所谓的 “假设性三段论的模式”。我们在此将两种模式并列展示。
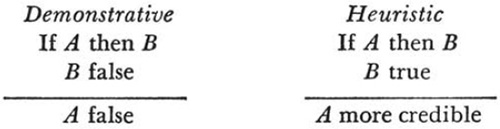
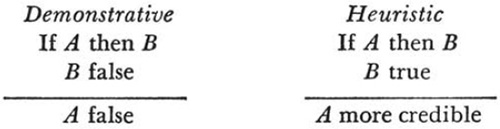
The comparison of these patterns may be instructive. It may grant us an insight, not easily obtainable elsewhere, into the nature of plausible (heuristic, inductive) reasoning.
对这些模式的比较可能是有启发的。它可能会让我们对可信的（启发式、归纳式）推理的性质有一个在其他地方不容易得到的洞察力。
Both patterns have the same first premise:
这两种模式都有相同的第一个前提。
They differ in the second premise. The statements:
它们在第二个前提下有所不同。这些说法：
|
B false |
B true |
|
B 假的 |
B真的 |
are exactly opposite to each other but they are of “similar logical nature,” they are on the same “logical level.” The great difference arises after the premises. The conclusions
是完全相反的，但它们具有 “相似的逻辑性质”，它们处于同一 “逻辑水平”。巨大的差异产生于前提之后。结论
|
A false |
A more credible |
|
A 假的 |
A 更可信 |
are on different logical levels and their relations to their respective premises are of a different logical nature.
处于不同的逻辑层次，它们与各自前提的关系具有不同的逻辑性质。
The conclusion of the demonstrative syllogism is of the same logical nature as the premises. Moreover, this conclusion is fully expressed and is fully supported by the premises. If my neighbor and I agree to accept the premises, we cannot reasonably disagree about accepting also the conclusion, however different our tastes or other convictions may be.
The conclusion of the heuristic syllogism differs from the premises in its logical nature; it is more vague, not so sharp, less fully expressed. This conclusion is comparable to a force, has direction and magnitude. It pushes us in a certain direction: A becomes more credible. The conclusion also has a certain strength: A may become much more credible, or just a little more credible. The conclusion is not fully expressed and is not fully supported by the premises. The direction is expressed and is implied by the premises, the magnitude is not. For any reasonable person, the premises involve that A becomes more credible (certainly not less credible). Yet my neighbor and I can honestly disagree how much more credible A becomes, since our temperaments, our backgrounds, and our unstated reasons may be different.
启发式三段论的结论在逻辑性质上与前提不同；它更模糊，不那么尖锐，表达得不那么充分。这个结论相当于一种力量，有方向和大小。它把我们推向了某个方向。A变得更加可信。这个结论也有一定的力度。A可能会变得更加可信，或者只是稍微可信一点。结论没有完全表达出来，也没有得到前提的完全支持。方向是表达出来的，而且是由前提所暗示的，幅度则不是。对于任何有理智的人来说，前提涉及到A变得更可信（当然不是更不可信）。然而，我和我的邻居可以诚实地不同意A变得更可信的程度，因为我们的脾气、我们的背景和我们未说明的原因可能是不同的。
In the demonstrative syllogism the premises constitute a full basis on which the conclusion rests. If both premises stand, the conclusion stands too. If we receive some new information that does not change our belief in the premises, it cannot change our belief in the conclusion.
在论证式三段论中，前提构成了结论赖以存在的全部基础。如果两个前提都成立，结论也成立。如果我们收到一些新的信息，而这些信息并没有改变我们对前提的信念，那么它也不能改变我们对结论的信念。
In the heuristic syllogism the premises constitute only one part of the basis on which the conclusion rests, the fully expressed, the “visible” part of the basis; there is an unexpressed, invisible part, formed by something else, by inarticulate feelings perhaps, or by unstated reasons. In fact, it can happen that we receive some new information that leaves our belief in both premises completely intact, but influences the trust we put in A in a way just opposite to that expressed in the conclusion. To find A more plausible on the ground of the premises of our heuristic syllogism is only reasonable. Yet tomorrow I may find grounds, not interfering at all with these premises, that make A appear less plausible, or even definitively refute it. The conclusion may be shaken and even overturned completely by commotions in the invisible parts of its foundation, although the premises, the visible part, stand quite firm.
These remarks seem to make somewhat more understandable the nature of heuristic, inductive, and other sorts of not demonstrative plausible reasoning, which appear so baffling and elusive when approached from the point of view of purely demonstrative logic. Many more concrete examples, the consideration of other kinds of heuristic syllogism, and an investigation of the concept of probability and other allied concepts seem to be necessary to complete the approach here chosen; cf. the author’s Mathematics and Plausible Reasoning.]
这些评论似乎使启发式、归纳式和其他种类的非证明性的合理推理的性质变得更容易理解，这些推理在从纯证明性逻辑的角度来探讨时显得如此令人困惑和难以捉摸。要完成这里所选择的方法，似乎还需要更多的具体例子，考虑其他种类的启发式三段论，以及对概率概念和其他相关概念的研究；参见作者的《数学与合理推理》。］
Heuristic reasons are important although they prove nothing. To clarify our heuristic reasons is also important although behind any reason clarified there are many others that remain obscure and are perhaps still more important.
启发式的理由很重要，尽管它们不能证明什么。澄清我们的启发式理由也很重要，尽管在任何被澄清的理由背后，还有许多其他的理由仍然模糊不清，也许仍然更重要。
1. Example. In a triangle, let r be the radius of the inscribed circle, R the radius of the circumscribed circle, and H the longest altitude. Then
1.例子。在一个三角形中，让r是内切圆的半径，R是外切圆的半径，H是最长的高度。那么
We have to prove (or disprove) this theorem9; we have a “problem to prove.”
我们必须证明（或反证）这个定理9；我们有一个 “需要证明的问题”。
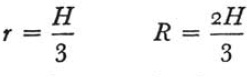
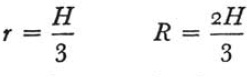
so that, in this case, the assertion is correct.
因此，在这种情况下，该断言是正确的。
If no other idea presents itself, we may test the more extended special case of isosceles triangles. The form of an isosceles triangle varies with the angle at the vertex and there are two extreme (or limiting) cases, the one in which the angle at the vertex becomes 0°, and the other in which it becomes 180°. In the first extreme case the base of the isosceles triangle vanishes and visibly
如果没有其他想法，我们可以测试等腰三角形的更多特殊情况。等腰三角形的形式随顶点的角度而变化，有两种极端（或极限）情况，一种是顶点的角度变成 0°，另一种是变成 180°。在第一种极端情况下，等腰三角形的底面消失了，而且明显的是
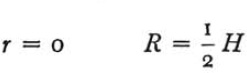
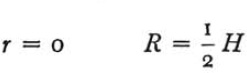
thus, the assertion is verified. In the second limiting case, however, all three heights vanish and
因此，该论断得到了验证。然而，在第二种极限情况下，所有三个高度都消失了，并且
The assertion is not verified. We have proved that the proposed theorem is false, and so we have solved our problem.
该断言没有得到验证。我们已经证明了所提出的定理是假的，所以我们的问题已经解决了。
By the way, it is clear that the assertion is also false for very flat isosceles triangles whose angle at the vertex is nearly 180° so that we may “officially” disregard the extreme cases whose consideration may appear as not quite “orthodox.”
顺便说一下，对于顶点角度接近 180°的非常平坦的等腰三角形来说，这个断言显然也是错误的，因此我们可以 “正式” 不考虑其考虑可能显得不大 “正统” 的极端情况。
2. “L’exception confirme la règle.” “The exception proves the rule.” We must take this widely known saying as a joke, laughing at the laxity of a certain sort of logic. If we take matters seriously, one exception is enough, of course, to refute irrefragably any would-be rule or general statement. The most usual and, in some respects, the best method to refute such a statement consists precisely in exhibiting an object that does not comply with it; such an object is called a counter-example by certain writers.
The allegedly general statement is concerned with a certain set of objects; in order to refute the statement we specialize, we pick out from the set an object that does not comply with it. The foregoing example (under 1) shows how it is done. We may examine at first any simple special case, that is, any object chosen more or less at random which we can easily test. If the test shows that the case is not in accordance with the general statement, the statement is refuted and our task finished. If, however, the object examined complies with the statement we may possibly derive some hint from its examination. We may receive the impression that the statement could be true, after all, and some suggestion in which direction we should seek the proof. Or, we may receive, as in our example under 1, some suggestion in which direction we should seek the counter-example, that is, which other special cases should we test. We may modify the case we have just examined, vary it, investigate some more extended special case, look around for extreme cases, as exemplified under 1.
所谓的一般陈述是关于某一组对象的；为了反驳我们所擅长的陈述，我们从这组对象中挑出一个不符合陈述的对象。前面的例子（1 下）显示了它是如何做到的。我们一开始可以检查任何简单的特例，也就是或多或少随机选择的任何对象，我们可以很容易地测试。如果测试结果显示，该案例不符合一般的陈述，那么该陈述就被驳斥了，我们的任务也就完成了。然而，如果被检验的对象符合声明，我们就有可能从其检验中得到一些提示。我们可能会得到这样的印象：声明毕竟是真实的，以及一些建议，我们应该在哪个方向寻求证明。或者，我们可能会收到，就像我们在 1 下的例子一样，一些建议，我们应该在哪个方向寻求反例，也就是说，我们应该测试哪些其他的特殊情况。我们可以修改我们刚刚检查过的案例，改变它，研究一些更广泛的特殊情况，寻找周围的极端情况，就像 1 下的例子。
Extreme cases are particularly instructive. If a general statement is supposed to apply to all mammals it must apply even to such an unusual mammal as the whale. Let us not forget this extreme case of the whale. Examining it, we may refute the general statement; there is a good chance for that, since such extreme cases are apt to be overlooked by the inventors of generalizations. If, however, we find that the general statement is verified even in the extreme case, the inductive evidence derived from this verification will be strong, just because the prospect of refutation was strong. Thus, we are tempted to reshape the saying from which we started: “Prospective exceptions test the rule.”
3. Example. Given the speeds of two ships and their positions at a certain moment; each ship steers a rectilinear course with constant speed. Find the distance of the two ships when they are nearest to each other.
3.例子。给出两艘船的速度和它们在某一时刻的位置；每艘船都以恒定的速度驶向一条直线。求两艘船最接近对方时的距离。
What is the unknown? The shortest distance between two moving bodies. The bodies have to be considered as material points.
什么是未知数？两个运动体之间的最短距离。这些物体必须被看作是物质点。
What are the data? The initial positions of the moving material points, and the speed of each. These speeds are constant in amount and direction.
这些数据是什么？移动的材料点的初始位置，以及每个点的速度。这些速度在数量和方向上是恒定的。
FIG. 19
图 19
What is the condition? The distance has to be ascertained when it is the shortest, that is, at the moment when the two moving points (ships) are nearest to each other.
什么是条件？距离必须在最短的时候被确定，也就是说，在两个运动点（船）最接近对方的时候。
Draw a figure. Introduce suitable notation. In Fig. 19, the points A and B mark the given initial positions of the two ships. The directed line-segments (vectors) AP and BQ represent the given speeds so that the first ship proceeds along the straight line through the points A and P, and covers the distance AP in unit time. The second ship travels similarly along the straight line BQ.
画一个图形。引入适当的符号。在图 19中，点A和B标志着两艘船的初始位置。有向线段（向量）AP和BQ代表给定的速度，使第一艘船沿着穿过A和P点的直线前进，并在单位时间内完成距离AP。第二艘船同样沿直线BQ行驶。
What is the unknown? The shortest distance of the two ships, the one traveling along AP and the other along BQ.
未知数是什么？两艘船的最短距离，一艘沿AP行驶，另一艘沿BQ行驶。
It is clear by now what we should find; yet, if we wish to use only elementary means, we may be still in the dark how we should find it. The problem is not too easy and its difficulty has some peculiar nuance which we may try to express by saying that “there is too much variety.” The initial positions, A and B, and the speeds, AP and BQ, can be given in various ways; in fact, the four points A, B, P, Q may be chosen arbitrarily. Now, whatever the data may be, the required solution must apply and we do not see yet how to fit the same solution to all these possibilities. Out of such feeling of “too much variety” this question and answer may eventually emerge:
我们应该找到什么，现在已经很清楚了；然而，如果我们只想使用基本的手段，我们可能仍然不知道应该如何找到它。这个问题并不太容易，它的困难有一些特殊的细微差别，我们可以尝试用 “种类太多” 来表达。初始位置A和B，以及速度AP和BQ，可以以各种方式给出；事实上，A、B、P、Q这四个点可以任意选择。现在，无论数据是什么，所需的解决方案必须适用，我们还不知道如何将同一解决方案适用于所有这些可能性。在这种 “种类太多” 的感觉中，这个问题和答案最终可能出现。
Could you imagine a more accessible related problem? A more special problem? Of course, there is the extreme special case in which one of the speeds vanishes. Yes, the ship in B may lay at anchor, Q may coincide with B. The shortest distance from the ship at rest to the moving ship is the perpendicular to the straight line along which the latter moves.
你能想象一个更容易获得的相关问题吗？一个更特殊的问题？当然，有一种极端的特殊情况，其中一个速度消失了。是的，B中的船可能躺在锚地，Q可能与B重合。从静止的船到移动的船的最短距离是与后者移动的直线的垂直线。
4. If the foregoing idea emerges with the premonition that there is more ahead and with the feeling that that extreme special case (which could appear as too simple to be relevant) has some role to play—then it is a bright idea indeed.
4. 如果上述想法是在预感到前面还有更多的东西，并且感觉到那个极端的特例（可能显得太简单而不相关）有一些作用，那么它确实是一个聪明的想法。
Here is a problem related to yours, that specialized problem you just solved. Could you use it? Could you use its result? Should you introduce some auxiliary element in order to make its use possible? It should be used, but how? How could the result of the case in which B is at rest be used in the case in which B is moving? Rest is a special case of motion. And motion is relative—and, therefore, whatever the given velocity of B may be I can consider B as being at rest! Here is the idea more clearly: If I impart to the whole system, consisting of both ships, the same uniform motion, the relative positions do not change, the relative distances remain the same, and so does especially the shortest relative distance of the two ships required by the problem. Now, I can impart a motion that reduces the speed of one of the ships to zero, and so reduces the general case of the problem to the special case just solved. Let me add a velocity, opposite to BQ but of the same amount, both to BQ and to AP. This is the auxiliary element that makes the use of the special result possible.
这里有一个与你有关的问题，就是你刚刚解决的那个专门问题。你能使用它吗？你能使用它的结果吗？你是否应该引入一些辅助元素，以便使其使用成为可能？它应该被使用，但如何使用？如何将B处于静止状态的情况下的结果用于B运动的情况下？静止是运动的一个特殊情况。而运动是相对的 —— 因此，无论B的给定速度是多少，我都可以认为B处于静止状态!这里的想法更清楚。如果我给由两艘船组成的整个系统赋予同样的匀速运动，相对位置不会改变，相对距离保持不变，特别是问题所要求的两艘船的最短相对距离也是如此。现在，我可以传授一个运动，使其中一艘船的速度降为零，从而将问题的一般情况降为刚刚解决的特殊情况。让我在BQ和AP上增加一个速度，与BQ相反，但数量相同。这是一个辅助因素，使特殊结果的使用成为可能。
FIG. 20
图 20
In order to solve our original problem (under 3, first lines) we have solved first another problem which we may call appropriately the auxiliary problem (under 3, last lines). This auxiliary problem is a special case of the original problem (the extreme special case in which one of the two ships is at rest). The original problem was proposed, the auxiliary problem invented in the course of the solution. The original problem looked hard, the solution of the auxiliary problem was immediate. The auxiliary problem was, as a special case, in fact much less ambitious than the original problem. How is it then possible that we were able to solve the original problem on the basis of the auxiliary problem? Because in reducing the original problem to the auxiliary problem, we added a substantial supplementary remark (on relativity of motion).
为了解决我们的原始问题（3 下，第一行），我们首先解决了另一个问题，我们可以适当地称之为辅助问题（3 下，最后一行）。这个辅助问题是原始问题的一个特例（即两艘船中有一艘处于静止状态的极端特例）。原来的问题被提出来了，辅助问题是在解决的过程中发明的。原来的问题看起来很难，而辅助问题的解决却很直接。作为一个特例，辅助问题实际上比原问题要小得多。那么，我们怎么可能在辅助问题的基础上解决原始问题呢？因为在将原问题还原为辅助问题时，我们增加了一个实质性的补充说明（关于运动的相对性）。
We succeeded in solving our original problem thanks to two remarks. First, we invented an advantageous auxiliary problem. Second, we discovered an appropriate supplementary remark to pass from the auxiliary problem to the original problem. We solved the proposed problem in two steps as we might cross a creek in two steps provided we were lucky enough to discover an appropriate stone in the middle which could serve as a momentary foothold.
我们成功地解决了我们最初的问题，这要归功于两点。首先，我们发明了一个有利的辅助问题。第二，我们发现了一个适当的补充说明，以便从辅助问题转到原始问题。我们分两步解决了所提出的问题，就像我们可能分两步渡过一条小河一样，只要我们足够幸运，在中间发现一块合适的石头，可以作为一个临时的立足点。
To sum up, we used the less difficult, less ambitious, special, auxiliary problem as a stepping stone in solving the more difficult, more ambitious, general, original problem.
总而言之，我们把难度较小、目标不高的特殊辅助性问题作为解决难度较大、目标较高的一般原始问题的垫脚石。
6. Specialization has many other uses which we cannot discuss here. It may be just mentioned that it can be useful in testing the solution (CAN YOU CHECK THE RESULT? 2).
6. 专业化还有许多其他用途，我们不能在此讨论。我们可以提到的是，它在测试解决方案时非常有用（你能检查结果吗？2）。
A somewhat primitive kind of specialization is often useful to the teacher. It consists in giving some concrete interpretation to the abstract mathematical elements of the problem. For instance, if there is a rectangular parallelepiped in the problem, the teacher may take the classroom in which he talks as example (section 8). In solid analytic geometry, a corner of the classroom may serve as the origin of coordinates, the floor and two walls as coordinate planes, two horizontal edges of the room and one vertical edge as coordinate axes. Explaining the notion of a surface of revolution, the teacher draws a curve with chalk on the door and opens it slowly. These are certainly simple tricks but nothing should be omitted that has some chance to bring home mathematics to the students: Mathematics being a very abstract science should be presented very concretely.
Subconscious work. One evening I wished to discuss with a friend a certain author but I could not remember the author’s name. I was annoyed, because I remembered fairly well one of his stories. I remembered also some story about the author himself which I wanted to tell; I remembered, in fact, everything except the name. Repeatedly, I tried to recollect that name but all in vain. The next morning, as soon as I thought of the annoyance of the evening before, the name occurred to me without any effort.
The reader, very likely, remembers some similar experience of his own. And, if he is a passionate problem-solver, he has probably had some similar experience with problems. It often happens that you have no success at all with a problem; you work very hard yet without finding anything. But when you come back to the problem after a night’s rest, or a few days’ interruption, a bright idea appears and you solve the problem easily. The nature of the problem matters little; a forgotten word, a difficult word from a crossword-puzzle, the beginning of an annoying letter, or the solution of a mathematical problem may occur in this way.
Such happenings give the impression of subconscious work. The fact is that a problem, after prolonged absence, may return into consciousness essentially clarified, much nearer to its solution than it was when it dropped out of consciousness. Who clarified it, who brought it nearer to the solution? Obviously, oneself, working at it subconsciously. It is difficult to give any other answer; although psychologists have discovered the beginnings of another answer which may turn out some day to be more satisfactory.
这种情况给人以潜意识工作的印象。事实是，一个问题在长期缺席后，可能会回到意识中，基本上得到澄清，比它从意识中消失时更接近其解决方案。谁澄清了它，谁使它更接近解决方案？很明显，是自己，在潜意识中工作。很难给出其他的答案；尽管心理学家已经发现了另一个答案的雏形，它可能在某一天会变得更加令人满意。
Whatever may or may not be the merits of the theory of subconscious work, it is certain that there is a limit beyond which we should not force the conscious reflection. There are certain moments in which it is better to leave the problem alone for a while. “Take counsel of your pillow” is an old piece of advice. Allowing an interval of rest to the problem and to ourselves, we may obtain more tomorrow with less effort. “If today will not, tomorrow may” is another old saying. But it is desirable not to set aside a problem to which we wish to come back later without the impression of some achievement; at least some little point should be settled, some aspect of the question somewhat elucidated when we quit working.
不管潜意识工作理论的优点是什么，可以肯定的是，有一个限度，我们不应该强迫有意识的思考。在某些时候，最好暂时不要管这个问题。“枕边人” 是一个古老的建议。让问题和我们自己有一段休息的时间，我们可以在明天以较少的努力获得更多。“如果今天不行，明天可以” 是另一句老话。但是，最好不要把一个我们希望以后再回来的问题搁置起来，否则会给人留下一些成就的印象；至少应该解决一些小问题，在我们放弃工作时，问题的某些方面得到一些澄清。
Only such problems come back improved whose solution we passionately desire, or for which we have worked with great tension; conscious effort and tension seem to be necessary to set the subconscious work going. At any rate, it would be too easy if it were not so; we could solve difficult problems just by sleeping and waiting for a bright idea.
只有这样的问题才会得到改善，而这些问题的解决是我们所热衷的，或者是我们为之付出了巨大的努力；有意识的努力和紧张似乎是启动潜意识工作的必要条件。不管怎么说，如果不是这样就太容易了；我们可以通过睡觉和等待一个聪明的想法来解决困难的问题。
Past ages regarded a sudden good idea as an inspiration, a gift of the gods. You must deserve such a gift by work, or at least by a fervent wish.10
过去的时代把突然出现的好主意视为一种灵感，，是神的礼物。你必须通过工作配得上这样的礼物，或者至少是通过热切的愿望。10
Elementary solid geometry considers two kinds of symmetry, symmetry with respect to a plane (called plane of symmetry), and symmetry with respect to a point (called center of symmetry). The human body appears to be fairly symmetrical but in fact it is not; many interior organs are quite unsymmetrically disposed. A statue may be completely symmetrical with respect to a vertical plane so that its two halves appear completely “interchangeable.”
初级实体几何学考虑了两种对称性，相对于一个平面的对称性（称为对称平面），以及相对于一个点的对称性（称为对称中心）。人体看起来是相当对称的，但事实上并非如此；许多内部器官的配置是相当不对称的。一座雕像可能相对于一个垂直平面是完全对称的，所以它的两半看起来完全 “可以互换”。
In a more general acceptance of the word, a whole is termed symmetric if it has interchangeable parts. There are many kinds of symmetry; they differ in the number of interchangeable parts, and in the operations which exchange the parts. Thus, a cube has high symmetry; its 6 faces are interchangeable with each other, and so are its 8 vertices, and so are its 12 edges. The expression
在对这个词的更广泛的接受中，如果一个整体有可互换的部分，它就被称为对称性。对称性有很多种；它们在可互换部分的数量和互换部分的操作上有所不同。因此，一个立方体具有高度对称性；它的 6 个面可以相互交换，它的 8 个顶点也可以相互交换，它的 12 条边也可以相互交换。表达式
is symmetric; any two of the three letters x, y, z can be interchanged without changing the expression.
是对称的；三个字母x、y、z中的任何两个可以互换而不改变表达式。
Symmetry, in a general sense, is important for our subject. If a problem is symmetric in some ways we may derive some profit from noticing its interchangeable parts and it often pays to treat those parts which play the same role in the same fashion (see AUXILIARY ELEMENTS, 3).
从一般意义上讲，对称性对我们的课题很重要。如果一个问题在某些方面是对称的，我们可以从注意到其可互换的部分中得到一些好处，而且以同样的方式处理那些发挥同样作用的部分往往是值得的（见辅助元素，3）。
Try to treat symmetrically what is symmetrical, and do not destroy wantonly any natural symmetry. However, we are sometimes compelled to treat unsymmetrically what is naturally symmetrical. A pair of gloves is certainly symmetrical; nevertheless, nobody handles the pair quite symmetrically, nobody puts on both gloves at the same time, but one after the other.
Symmetry may also be useful in checking results; see section 14.
对称性在检查结果时也可能是有用的，见第 14 节。
Terms, old and new, describing the activity of solving problems are often ambiguous. The activity itself is familiar to everybody and it is often discussed but, as other mental activities, it is difficult to describe. In the absence of a systematic study there are no technical terms to describe it, and certain usual half-technical terms often add to the confusion because they are used in different meanings by different authors.
The following short list includes a few new terms used and a few old terms avoided in the present study, and also some old terms retained despite their ambiguity.
下面的简短清单包括本研究中使用的一些新术语和避免使用的一些旧术语，还有一些旧术语尽管有歧义，但还是保留了下来。
The reader may be confused by the following discussion of terminology unless his notions are well anchored in examples.
读者可能会被下面的术语讨论所迷惑，除非他的概念被很好地固定在例子中。
1. Analysis is neatly defined by PAPPUS, and it is a useful term, describing a typical way of devising a plan, starting from the unknown (or the conclusion) and working backwards, toward the data (or the hypothesis). Unfortunately, the word has acquired very different meanings (for instance, of mathematical, chemical, logical analysis) and therefore, it is regretfully avoided in the present study.
1.分析是由PAPPUS整齐地定义的，它是一个有用的术语，描述了一种典型的设计计划的方式，从未知（或结论）开始，向后努力，朝着数据（或假设）前进。不幸的是，这个词已经获得了非常不同的含义（例如，数学、化学、逻辑分析），因此，在本研究中遗憾地避免了这个词。
2. Condition links the unknown of a “problem to find” to the data (see PROBLEMS TO FIND, PROBLEMS TO PROVE, 3). In this meaning, it is a clear, useful and unavoidable term. It is often necessary to decompose the condition into several parts [into parts (I) and (II) in the examples DECOMPOSING AND RECOMBINING, 7, 8]. Now, each part of the condition is usually called a condition. This ambiguity which is sometimes embarrassing could be easily avoided by introducing some technical term to denote the parts of the whole condition; for instance, such a part could be called a “clause.”
3. Hypothesis denotes an essential part of a mathematical theorem of the more usual kind (see PROBLEMS TO FIND, PROBLEMS TO PROVE, 4). The term, in this meaning, is perfectly clear and satisfactory. The difficulty is that each part of the hypothesis is also called a hypothesis so that the hypothesis may consist of several hypotheses. The remedy would be to call each part of the whole hypothesis a “clause,” or something similar. (Compare the foregoing remark on “condition.”)
3.假设表示更常见的数学定理的一个重要部分（见 “发现问题”、“证明问题”，4）。在这个意义上，这个术语是完全清晰和令人满意的。困难的是，假说的每一部分也被称为假说，因此，假说可能由几个假说组成。补救办法是将整个假说的每一部分称为 “条款”，或类似的东西。（比较前面关于 “条件” 的评论）。
4. Principal parts of a problem are defined in PROBLEMS TO FIND, PROBLEMS TO PROVE, 3, 4.
4. 问题的主要部分在 “发现问题”、“证明问题”、“3、4” 中定义。
5. Problem to find, problem to prove are a pair of new terms, introduced regretfully to replace historical terms whose meaning, however, is confused beyond redemption by current usage. In Latin versions of Greek mathematical texts, the common name for both kinds of problems is “propositio”; a “problem to find” is called “problema,” and a “problem to prove” “theorema.” In old-fashioned mathematical language, the words proposition, problem, theorem have still this “Euclidean” meaning, but this is completely changed in modern mathematical language; this justifies the introduction of new terms.
5.找到的问题、证明的问题是一对新术语，遗憾地被引入以取代历史上的术语，然而，这些术语的含义被目前的用法混淆得无法挽回。在希腊数学文本的拉丁文版本中，这两种问题的通用名称是 “propositio”；“要找的问题” 被称为 “problema”，“要证明的问题” 被称为 “theorema”。在老式的数学语言中，命题、问题、定理这些词仍然具有这种 “欧几里得” 的含义，但这在现代数学语言中完全改变了；这就证明了引入新术语的必要性。
6. Progressive reasoning was used in various meanings by various authors, and in the old meaning of “synthesis” (see 9) by some authors. The latter usage is defensible but the term is avoided here.
6.渐进式推理被不同的作者用在不同的意义上，也被一些作者用在 “综合”（见 9）的旧意义上。后者的用法是可以辩护的，但这里避免使用这个词。
8. Solution is a completely clear term if taken in its purely mathematical meaning; it denotes any object satisfying the condition of a “problem to find.” Thus, the solutions of the equation x2 − 3x + 2 = 0 are its roots, the numbers 1 and 2. Unfortunately, the word has also other meanings which are not purely mathematical and which are used by mathematicians along with its mathematical meaning. Solution may also mean the “process of solving the problem” or the “work done in solving the problem”; we use the word in this meaning when we talk about a “difficult solution.” Solution may also mean the result of the work done in solving the problem; we may use the word in this meaning when we talk about a “beautiful solution.” Now, it may happen that we have to talk in the same sentence about the object satisfying the condition of the problem, about the work of obtaining it, and about the result of this work; if we yield to the temptation to call all three things “solution” the sentence cannot be too clear.
8. 如果从纯粹的数学意义上看，解是一个完全明确的术语；它表示任何满足 “寻找问题” 条件的对象。因此，方程x2-3x+2=0 的解决方案是其根，即数字 1 和 2。不幸的是，这个词也有其他的含义，这些含义并不纯粹是数学上的，而是被数学家与数学含义一起使用。解决方案也可以指 “解决问题的过程” 或 “解决问题的工作”；当我们谈论 “困难的解决方案” 时，我们使用这个词的含义。解决方案也可以指在解决问题过程中所做的工作的结果；当我们谈论一个 “美丽的解决方案” 时，我们可以在这个意义上使用这个词。现在，可能发生的情况是，我们必须在同一个句子中谈论满足问题条件的对象，谈论获得它的工作，以及这个工作的结果；如果我们屈服于诱惑，把所有这三件事都称为 “解决方案”，这个句子就不会太清楚。
9. Synthesis is used by PAPPUS in a well defined meaning which would deserve to be conserved. The term is, however, regretfully avoided in the present study, for the same reasons as its counterpart “analysis” (see under 1).
9.PAPPUS使用的 “合成” 一词含义明确，应予保留。然而，令人遗憾的是，在本研究中，这个词被避免了，原因与它的对应词 “分析” 相同（见第 1 部分）。
1. In order to recall the operation of the test, let us consider the frustum of a right circular cone. Let
1. 为了回顾测试的操作，让我们考虑一个右圆锥体的外壳。设
R be the radius of the lower base,
r the radius of the upper base,
h the altitude of the frustum,
S the area of the lateral surface of the frustum.
R为下层底座的半径，
r 为上层底座的半径，
h 为壳的高度，
S 为壳的侧表面的面积。
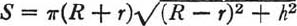
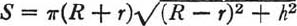
to which we wish to apply the test by dimension.
我们希望对其进行维度测试。
The dimension of a geometric quantity is easily visible. Thus, R, r, h are lengths, they are measured in centimeters if we use scientific units, their dimension is cm. The area S is measured in square centimeters, its dimension is cm2. Now, π = 3.14159 . . . is a mere number; if we wish to ascribe a dimension to a purely numerical quantity it must be cm0 = 1.
一个几何量的尺寸是很容易看到的。因此，R、r、h是长度，如果我们使用科学单位，它们的测量单位是厘米，其尺寸是cm。面积S的单位是平方厘米，它的尺寸是cm2。现在，π=3.14159 …… 是一个单纯的数字；如果我们想给一个纯粹的数字量赋予一个尺寸，它必须是cm0=1。
Each term of a sum must have the same dimension which is also the dimension of the sum. Thus, R, r, and R + r have the same dimension, namely cm. The two terms (R − r)2 and h2 have the same dimension (as they must), cm2.
和的每一项都必须有相同的尺寸，这也是和的尺寸。因此，R、r和R+r有相同的尺寸，即cm。两个项（R-r）2和h2具有相同的维度（因为它们必须），即cm2。
The dimension of a product is the product of the dimensions of its factors, and there is a similar rule about powers. Replacing the quantities by their dimensions on both sides of the formula that we are testing, we obtain
积的尺寸是其因子尺寸的乘积，关于幂也有一个类似的规则。将我们要测试的公式两边的量替换成它们的尺寸，我们可以得到
This being visibly so, the test could not detect any error in the formula. The formula passed the test.
由于明显如此，测试无法检测到公式中的任何错误。该公式通过了测试。
For other examples, see section 14, and CAN YOU CHECK THE RESULT? 2.
其他例子见第 14 节，你能检查出结果吗？2.
2. We may apply the test by dimension to the final result of a problem or to intermediary results, to our own work or to the work of others (very suitable in tracing mistakes in examination papers), and also to formulas that we recollect and to formulas that we guess.
2. 我们可以按维度对问题的最终结果或中间结果，对我们自己的工作或他人的工作（非常适用于追踪试卷中的错误），以及对我们回忆的公式和我们猜测的公式进行检验。
If you recollect the formulas 4πr2 and 4πr3/3 for the area and the volume of the sphere, but are not quite sure which is which, the test by dimension easily removes the doubt.
如果你记得球体面积和体积的公式 4πr2和 4πr3/3，但不太确定哪个是哪个，那么通过尺寸测试就可以轻松消除疑问。
3. The test by dimension is even more important in physics than in geometry.
3. 按维度测试在物理学中甚至比在几何学中更重要。
Mechanical considerations show that T depends on l and g alone. But what is the form of the dependence? We may remember or guess that
机械考虑表明，T只取决于l和g。但这种依赖关系的形式是什么呢？我们可能记得或猜测到
where c, m, n are certain numerical constants. That is, we suppose that T is proportional to certain powers, lm, gn, of l and g.
其中c、m、n是某些数字常数。也就是说，我们假设T与l和g的某些幂，lm，gn成正比。
We look at the dimensions. As T is a time, it is measured in seconds, its dimension is sec. The dimension of the length l is cm, the dimension of the acceleration g is cm sec−2, and the dimension of the numerical constant c is 1. The test by dimension yields the equation
我们看一下尺寸。由于T是一个时间，它是以秒为单位的，它的尺寸是秒。长度l的尺寸是cm，加速度g的尺寸是cm sec-2，数值常数c的尺寸是 1。
or
或
Now, we must have the same powers of the fundamental units cm and sec on both sides, and thus we obtain
现在，我们必须在两边有相同的基本单位厘米和秒的权力，因此我们得到
and hence
因此
Therefore, the formula for the period T must have the form
因此，周期T的公式必须具有以下形式
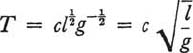
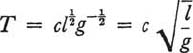
The test by dimension yields much in this case but it cannot yield everything. First, it gives no information about the value of the constant c (which is, in fact, 2π). Second, it gives no information about the limits of validity; the formula is valid only for small oscillations of the pendulum and only approximately (it is exact for “infinitely small” oscillations). In spite of these limitations, there is no doubt that the consideration of the dimensions has allowed us to foresee quickly and with the most elementary means an essential part of a result whose exhaustive treatment demands much more advanced means. And this is so in many similar cases.
For him, the most important part of the work is to look back at the completed solution. Surveying the course of his work and the final shape of the solution, he may find an unending variety of things to observe. He may meditate upon the difficulty of the problem and about the decisive idea; he may try to see what hampered him and what helped him finally. He may look out for simple intuitive ideas: Can you see it at a glance? He may compare and develop various methods: Can you derive the result differently? He may try to clarify his present problem by comparing it to problems formerly solved; he may try to invent new problems which he can solve on the basis of his just completed work: Can you use the result, or the method, for some other problem? Digesting the problems he solved as completely as he can, he may acquire well ordered knowledge, ready to use.
对他来说，工作中最重要的部分是回头看已完成的解决方案。观察他的工作过程和解决方案的最终形态，他可能会发现有各种无尽的东西需要观察。他可能会思考问题的难度和决定性的想法；他可能会尝试看看什么阻碍了他，什么最终帮助了他。他可能会寻找简单的直觉想法。你能一目了然地看到它吗？他可能会比较和发展各种方法。你能以不同的方式推导出结果吗？他可能试图通过与以前解决的问题进行比较来澄清他现在的问题；他可能试图发明新的问题，在他刚刚完成的工作的基础上解决。你能把这个结果或这个方法用于其他问题吗？尽可能完整地消化他所解决的问题，他可能会获得有序的知识，随时可以使用。
The future mathematician learns, as does everybody else, by imitation and practice. He should look out for the right model to imitate. He should observe a stimulating teacher. He should compete with a capable friend. Then, what may be the most important, he should read not only current textbooks but good authors till he finds one whose ways he is naturally inclined to imitate. He should enjoy and seek what seems to him simple or instructive or beautiful. He should solve problems, choose the problems which are in his line, meditate upon their solution, and invent new problems. By these means, and by all other means, he should endeavor to make his first important discovery: he should discover his likes and his dislikes, his taste, his own line.
The intelligent problem-solver often asks himself questions similar to those contained in our list. He, perhaps, discovered questions of this sort by himself; or, having heard such a question from somebody, he discovered its proper use by himself. He is possibly not conscious at all that he repeats the same stereotyped question again and again. Or the question is his particular pet; he knows that the question is part of his mental attitude appropriate in such and such a phase of the work, and he summons up the right attitude by asking the right question.
The intelligent problem-solver may find the questions and suggestions of our list useful. He may understand quite well the explanations and examples illustrating a certain question, he may suspect the proper use of the question; but he cannot attain real understanding unless he comes across the procedure that the question tries to provoke in his own work and, by having experienced its usefulness, discovers the proper use of the question for himself.
聪明的问题解决者可能会发现我们清单上的问题和建议很有用。他可能会很好地理解说明某个问题的解释和例子，他可能会怀疑这个问题的正确用途；但是，除非他在自己的工作中遇到这个问题试图引发的程序，并且通过体验其有用性，发现这个问题对自己的正确用途，否则他无法达到真正的理解。
The intelligent problem-solver should be prepared to ask all questions of the list but he should ask none unless he is prompted to do so by careful consideration of the problem at hand and by his own unprejudiced judgment. In fact, he must recognize by himself whether the present situation is sufficiently similar or not to some other situation in which he saw the question successfully applied.
The intelligent problem-solver tries first of all to understand the problem as fully and as clearly as he can. Yet understanding alone is not enough; he must concentrate upon the problem, he must desire earnestly to obtain its solution. If he cannot summon up real desire for solving the problem he would do better to leave it alone. The open secret of real success is to throw your whole personality into your problem.
聪明的问题解决者首先试图尽可能充分和清楚地了解问题。然而，仅仅理解是不够的；他必须专注于这个问题，他必须认真地渴望得到问题的解决。如果他不能唤起解决这个问题的真正愿望，他最好不要管它。真正成功的公开秘密是将你的整个人格投入到你的问题中。
First, to see that the present step of the argument is correct.
首先，要看到论证的本步骤是正确的。
Second, to see the purpose of the present step.
第二，要看到本步骤的目的。
The intelligent listener to a mathematical lecture has the same wishes. If he cannot see that the present step of the argument is correct and even suspects that it is, possibly, incorrect, he may protest and ask a question. If he cannot see any purpose in the present step, nor suspect any reason for it, he usually cannot even formulate a clear objection, he does not protest, he is just dismayed and bored, and loses the thread of the argument.
聪明的听众在听数学讲座时也有同样的愿望。如果他看不出目前的论证步骤是正确的，甚至怀疑它可能是不正确的，他可能会提出抗议并提出问题。如果他看不到当前步骤的任何目的，也不怀疑任何理由，他通常甚至无法提出明确的反对意见，他不会抗议，只是感到沮丧和无聊，并失去了论证的线索。
The intelligent teacher and the intelligent author of textbooks should bear these points in mind. To write and speak correctly is certainly necessary; but it is not sufficient. A derivation correctly presented in the book or on the blackboard may be inaccessible and uninstructive, if the purpose of the successive steps is incomprehensible, if the reader or listener cannot understand how it was humanly possible to find such an argument, if he is not able to derive any suggestion from the presentation as to how he could find such an argument by himself.
The questions and suggestions of our list may be useful to the author and to the teacher in emphasizing the purpose and the motives of his argument. Particularly useful in this respect is the question: DID WE USE ALL THE DATA? The author or the teacher may show by this question a good reason for considering the datum that has not been used heretofore. The reader or the listener can use the same question in order to understand the author’s or the teacher’s reason for considering such and such an element, and he may feel that, asking this question, he could have discovered this step of the argument by himself.
我们清单上的问题和建议可能对作者和教师强调其论证的目的和动机有帮助。在这方面特别有用的问题是。我们是否使用了所有的数据？作者或教师可以通过这个问题表明，有一个很好的理由来考虑以前没有使用过的数据。读者或听众可以用同样的问题来理解作者或老师考虑这样那样的因素的原因，他可能会觉得，问了这个问题，他就可以自己发现论证的这个步骤。
The traditional mathematics professor of the popular legend is absentminded. He usually appears in public with a lost umbrella in each hand. He prefers to face the blackboard and to turn his back on the class. He writes a, he says b, he means c; but it should be d. Some of his sayings are handed down from generation to generation.
“In order to solve this differential equation you look at it till a solution occurs to you.”
“为了解决这个微分方程，你看着它，直到你想到一个解决方案。”
“This principle is so perfectly general that no particular application of it is possible.”
“这一原则是如此完美的一般性，以至于不可能对其进行特别的应用。”
“Geometry is the art of correct reasoning on incorrect figures.”
“几何学是对不正确的数字进行正确推理的艺术”。
“My method to overcome a difficulty is to go round it.”
“我克服困难的方法是绕过它”。
“What is the difference between method and device? A method is a device which you use twice.”
“方法和设备的区别是什么？方法是一种装置，你要使用两次。”
After all, you can learn something from this traditional mathematics professor. Let us hope that the mathematics teacher from whom you cannot learn anything will not become traditional.
毕竟，你可以从这位传统的数学教授那里学到一些东西。让我们希望，你不能从他那里学到任何东西的数学老师不会成为传统。
Variation of the problem. An insect (as mentioned elsewhere) tries to escape through the windowpane, tries the same hopeless thing again and again, and does not try the next window which is open and through which it came into the room. A mouse may act more intelligently; caught in the trap, he tries to squeeze through between two bars, then between the next two bars, then between other bars; he varies his trials, he explores various possibilities. A man is able, or should be able, to vary his trials still more intelligently, to explore the various possibilities with more understanding, to learn by his errors and shortcomings. “Try, try again” is popular advice. It is good advice. The insect, the mouse, and the man follow it; but if one follows it with more success than the others it is because he varies his problem more intelligently.
1. At the end of our work, when we have obtained the solution, our conception of the problem will be fuller and more adequate than it was at the outset. Desiring to proceed from our initial conception of the problem to a more adequate, better adapted conception, we try various standpoints and we view the problem from different sides.
1. 在我们的工作结束时，当我们获得解决方案时，我们对问题的概念将比一开始时更全面、更充分。我们希望从最初的问题概念发展到一个更充分、更合适的概念，我们尝试各种立场，从不同的角度看待问题。
Success in solving the problem depends on choosing the right aspect, on attacking the fortress from its accessible side. In order to find out which aspect is the right one, which side is accessible, we try various sides and aspects, we vary the problem.
解决问题的成功取决于选择正确的方面，取决于从其可进入的一面攻击堡垒。为了找出哪个方面是正确的，哪个方面是可以进入的，我们尝试各种侧面和方面，我们改变问题。
2. Variation of the problem is essential. This fact can be explained in various ways. Thus, from a certain point of view, progress in solving the problem appears as mobilization and organization of formerly acquired knowledge. We have to extract from our memory and to work into the problem certain elements. Now, variation of the problem helps us to extract such elements. How?
2. 问题的变化是必不可少的。这一事实可以用各种方式来解释。因此，从某种角度来看，解决问题的进展似乎是对以前获得的知识的调动和组织。我们必须从我们的记忆中提取某些元素，并将其运用到问题中。现在，问题的变化有助于我们提取这些要素。如何提取？
We remember things by a kind of “action by contact,” called “mental association”; what we have in our mind at present tends to recall what was in contact with it at some previous occasion. (There is no space and no need to state more neatly the theory of association, or to discuss its limitations.) Varying the problem, we bring in new points, and so we create new contacts, new possibilities of contacting elements relevant to our problem.
3. We cannot hope to solve any worth-while problem without intense concentration. But we are easily tired by intense concentration of our attention upon the same point. In order to keep the attention alive, the object on which it is directed must unceasingly change.
3. 如果不集中注意力，我们就不能指望解决任何有价值的问题。但我们很容易因注意力集中在同一点上而感到疲劳。为了保持注意力的活力，它所指向的对象必须不断地变化。
If our work progresses, there is something to do, there are new points to examine, our attention is occupied, our interest is alive. But if we fail to make progress, our attention falters, our interest fades, we get tired of the problem, our thoughts begin to wander, and there is danger of losing the problem altogether. To escape from this danger we have to set ourselves a new question about the problem.
如果我们的工作有进展，就有事情可做，就有新的观点可研究，我们的注意力就会被占据，我们的兴趣就会活跃。但是，如果我们不能取得进展，我们的注意力就会减弱，我们的兴趣就会消退，我们就会对这个问题感到厌倦，我们的思想就会开始游荡，就有可能完全失去这个问题。为了摆脱这种危险，我们必须为自己设定一个关于这个问题的新问题。
The new question unfolds untried possibilities of contact with our previous knowledge, it revives our hope of making useful contacts. The new question reconquers our interest by varying the problem, by showing some new aspect of it.
新问题展开了与我们以前的知识接触的未曾尝试过的可能性，它使我们恢复了进行有益接触的希望。新问题通过改变问题，通过展示问题的某些新方面，重新征服了我们的兴趣。
4. Example. Find the volume of the frustum of a pyramid with square base, being given the side of the lower base a, the side of the upper base b, and the altitude of the frustum h.
4.例子。给出下底的边a，上底的边b，以及底面的高度h，求一个正方形底面的金字塔的体积。
The problem may be proposed to a class familiar with the formulas for the volume of prism and pyramid. If the students do not come forward with some idea of their own, the teacher may begin with varying the data of the problem. We start from a frustum with a > b. What happens when b increases till it becomes equal to a? The frustum becomes a prism and the volume in question becomes a2h. What happens when b decreases till it becomes equal to 0? The frustum becomes a pyramid and the volume in question becomes a2h/3.
This variation of the data contributes, first of all, to the interest of the problem. Then, it may suggest using, in some way or other, the results quoted about prism and pyramid. At any rate, we have found definite properties of the final result; the final formula must be such that it reduces to a2h for b = a and to a2h/3 for b = 0. It is an advantage to foresee properties of the result we are trying to obtain. Such properties may give valuable suggestions and, in any case, when we have found the final formula we shall be able to test it. We have thus, in advance, an answer to the question: CAN YOU CHECK THE RESULT? (See there, under 2.)
数据的这种变化，首先有助于提高问题的趣味性。然后，它可能建议以某种方式使用所引用的关于棱柱和金字塔的结果。无论如何，我们已经发现了最终结果的明确属性；最终公式必须是这样的：当b=a时，它还原为a2h，当b=0 时，还原为a2h/3。这些属性可能会提供有价值的建议，而且在任何情况下，当我们找到最后的公式时，我们将能够测试它。这样，我们就提前得到了一个问题的答案。你能检验这个结果吗？（见那里的第 2 节。）
5. Example. Construct a trapezoid being given its four sides a, b, c, d.
5.例子。给出梯形的四条边a、b、c、d，构建一个梯形。
Let a be the lower base and c the upper base; a and c are parallel but unequal, b and d are not parallel. If there is no other idea, we may begin with varying the data.
设a为下基，c为上基；a和c平行但不相等，b和d不平行。如果没有其他想法，我们可以从改变数据开始。
We start from a trapezoid with a > c. What happens when c decreases till it becomes equal to 0? The trapezoid degenerates into a triangle. Now a triangle is a familiar and simple figure, which we can construct from various data; there could be some advantage in introducing this triangle into the figure. We do so by drawing just one auxiliary line, a diagonal of the trapezoid (Fig. 21). Examining the triangle we find however that it is scarcely useful; we know two sides, a and d, but we should have three data.
我们从一个a>c的梯形开始，当c减小到等于 0 时会发生什么？梯形会退化为三角形。现在，三角形是一个熟悉而简单的图形，我们可以从各种数据中构建它；将这个三角形引入图形中可能有一些好处。我们只需画一条辅助线，即梯形的对角线就可以做到这一点（图 21）。然而，审视这个三角形，我们发现它几乎没有什么用处；我们知道两条边，a和d，但我们应该有三个数据。
Let us try something else. What happens when c increases till it becomes equal to a? The trapezoid becomes a parallelogram. Could we use it? A little examination (see Fig. 22) directs our attention to the triangle which we have added to the original trapezoid when drawing the parallelogram. This triangle is easily constructed; we know three data, its three sides b, d, and a − c.
让我们试试别的东西。当c增加到与a相等时会发生什么？梯形变成了平行四边形。我们可以使用它吗？稍微观察一下（见图 22），我们就会注意到我们在画平行四边形时在原来的梯形上增加的三角形。这个三角形很容易构建；我们知道三个数据，它的三条边b、d和a-c。
FIG. 21
图 21
FIG. 22
图 22
Varying the original problem (construction of the trapezoid) we have been led to a more accessible auxiliary problem (construction of the triangle). Using the result of the auxiliary problem we easily solve our original problem (we have to complete the parallelogram).
改变原来的问题（梯形的构造），我们被引导到一个更容易理解的辅助问题（三角形的构造）。利用辅助问题的结果，我们很容易解决我们的原始问题（我们必须完成平行四边形）。
Our example is typical. It is also typical that our first attempt failed. Looking back at it, we may see however that that first attempt was not so useless. There was some idea in it; in particular, it gave us an opportunity to think of the construction of a triangle as means to our end. In fact, we arrived at our second, successful trial by modifying our first, unsuccessful trial. We varied c; we first tried to decrease it, then to increase it.
6. As in the foregoing example, we often have to try various modifications of the problem. We have to vary, to restate, to transform it again and again till we succeed eventually in finding something useful. We may learn by failure; there may be some good idea in an unsuccessful trial, and we may arrive at a more successful trial by modifying an unsuccessful one. What we attain after various trials is very often, as in the foregoing example, a more accessible auxiliary problem.
6. 就像前面的例子一样，我们经常要尝试对问题进行各种修改。我们必须一次又一次地改变、重述、改造它，直到我们最终成功地找到有用的东西。我们可以从失败中学习；在一个不成功的试验中可能有一些好的想法，我们可能通过修改一个不成功的试验而达到一个更成功的试验。在各种试验之后，我们所得到的往往是，就像前面的例子一样，一个更容易获得的辅助问题。
7. There are certain modes of varying the problem which are typically useful, as going back to the DEFINITION, DECOMPOSING AND RECOMBINING, introducing AUXILIARY ELEMENTS, GENERALIZATION, SPECIALIZATION, and the use of ANALOGY.
7. 有一些改变问题的模式通常是有用的，如回到定义，分解和重新组合，引入辅助元素，通用化，专业化，以及使用模拟。
8. What we said a while ago (under 3) about new questions which may reconquer our interest is important for the proper use of our list.
8. 我们不久前（在第 3 节下）所说的关于可能重新引起我们兴趣的新问题，对正确使用我们的清单很重要。
A teacher may use the list to help his students. If the student progresses, he needs no help and the teacher should not ask him any questions, but allow him to work alone which is obviously better for his independence. But the teacher should, of course, try to find some suitable question or suggestion to help him when he gets stuck. Because then there is danger that the student will get tired of his problem and drop it, or lose interest and make some stupid blunder out of sheer indifference.
老师可以用这个清单来帮助他的学生。如果学生进步了，他就不需要帮助，老师不应该问他任何问题，而是让他独自工作，这显然更有利于他的独立性。但是，老师当然应该努力找到一些合适的问题或建议来帮助他，当他被卡住时。因为这样一来，学生就有可能对他的问题感到厌烦而放弃，或者失去兴趣，因漠不关心而犯一些愚蠢的错误。
We may use the list in solving our own problems. To use it properly we proceed as in the former case. When our progress is satisfactory, when new remarks emerge spontaneously, it would be simply stupid to hamper our spontaneous progress by extraneous questions. But when our progress is blocked, when nothing occurs to us, there is danger that we may get tired of our problem. Then it is time to think of some general idea that could be helpful, of some question or suggestion of the list that might be suitable. And any question is welcome that has some chance of showing a new aspect of the problem; it may reconquer our interest, it may keep us working and thinking.
What are the data? What is given? What have you?
数据是什么？给了什么？你有什么？
What is the condition? By what condition is the unknown linked to the data?
什么是条件？未知数是通过什么条件与数据相联系的？
These questions may be used by the teacher to test the understanding of the problem; the student should be able to answer them clearly. Moreover, they direct the student’s attention to the principal parts of a “problem to find,” the unknown, the data, the condition. As the consideration of these parts may be necessary again and again, the questions may be often repeated in the later phases of the solution. (Examples in sections 8, 10, 18, 20; SETTING UP EQUATIONS, 3, 4; PRACTICAL PROBLEMS, 1; PUZZLES; and elsewhere.)
老师可以用这些问题来检验学生对问题的理解；学生应该能够清楚地回答这些问题。此外，这些问题将学生的注意力引向 “要找的问题” 的主要部分：未知数、数据、条件。由于对这些部分的考虑可能需要反复进行，所以在解决问题的后期阶段，这些问题可能经常被重复。（例子见第 8、10、18、20 节；设置方程，3、4；实际问题，1；猜谜；以及其他地方）。
The questions are of the greatest importance for the problem-solver. He checks his own understanding of the problem, he focuses his attention on this or that principal part of the problem. The solution consists essentially in linking the unknown to the data. Therefore, the problem-solver has to focus those elements again and again, asking: What is the unknown? What are the data?
这些问题对解决问题的人来说是最重要的。他检查自己对问题的理解，他把注意力集中在问题的这个或那个主要部分。解决方案主要包括将未知的东西与数据联系起来。因此，解决问题的人必须一次又一次地关注这些因素，问：“什么是未知的？未知是什么？数据是什么？
The problem may have many unknowns, or the condition may have various parts which must be considered separately, or it may be desirable to consider some datum by itself. Therefore, we may use various modifications of our questions, as: What are the unknowns? What is the first datum? What is the second datum? What are the various parts of the condition? What is the first clause of the condition?
The principal parts of a “problem to prove” are the hypothesis and the conclusion, and the corresponding questions are: What is the hypothesis? What is the conclusion? We may need some variation of verbal expression or modification of these frequently useful questions as: What do you assume? What are the various parts of your assumption? (Example in section 19.)
一个 “需要证明的问题” 的主要部分是假设和结论，相应的问题是。假设是什么？结论是什么？我们可能需要对这些经常有用的问题进行一些变化的口头表达或修改，如：。你的假设是什么？你的假设的各个部分是什么？（例子见第 19 节）。
Why proofs? There is a traditional story about Newton: As a young student, he began the study of geometry, as was usual in his time, with the reading of the Elements of Euclid. He read the theorems, saw that they were true, and omitted the proofs. He wondered why anybody should take pains to prove things so evident. Many years later, however, he changed his opinion and praised Euclid.
The story may be authentic or not, yet the question remains: Why should we learn, or teach, proofs? What is preferable: no proof at all, or proofs for everything, or some proofs? And, if only some proofs, which proofs?
这个故事可能是真实的或不真实的，然而问题仍然存在。我们为什么要学习，或教授证明？什么是最好的：完全没有证明，还是对所有事物都有证明，或者一些证明？如果只有一些证明，那么哪些证明呢？
1. Complete proofs. For a logician of a certain sort only complete proofs exist. What intends to be a proof must leave no gaps, no loopholes, no uncertainty whatever, or else it is no proof. Can we find complete proofs according to such a high standard in everyday life, or in legal procedure, or in physical science? Scarcely. Thus, it is difficult to understand how we could acquire the idea of such a strictly complete proof.
1.完整的证明。对于某类逻辑学家来说，只有完整的证明存在。打算成为证明的东西必须不留下任何空白，不留下任何漏洞，不留下任何不确定性，否则就不是证明。在日常生活中，或在法律程序中，或在物理科学中，我们能找到符合如此高标准的完整证明吗？几乎不可能。因此，很难理解我们是如何获得这种严格意义上的完整证明的想法的。
We may say, with a little exaggeration, that humanity learned this idea from one man and one book: from Euclid and his Elements. In any case, the study of the elements of plane geometry yields still the best opportunity to acquire the idea of rigorous proof.
我们可以略微夸张地说，人类从一个人和一本书中学到了这种思想：从欧几里德和他的《元素》中。在任何情况下，对平面几何要素的研究仍然是获得严格证明思想的最佳机会。
FIG. 23
图 23
The angles of the triangle at B and at C are equal to certain angles at A, as is emphasized in the figure, since alternate angles are equal in general. The three angles of the triangle are equal to three angles with a common vertex A, forming a straight angle, or two right angles; and so the theorem is proved.
三角形在B处和C处的角与A处的某些角相等，正如图中所强调的那样，因为交替的角一般都是相等的。三角形的三个角与有共同顶点A的三个角相等，形成一个直角，或两个直角；因此定理得到了证明。
If a student has gone through his mathematics classes without having really understood a few proofs like the foregoing one, he is entitled to address a scorching reproach to his school and to his teachers. In fact, we should distinguish between things of more and less importance. If the student failed to get acquainted with this or that particular geometric fact, he did not miss so much; he may have little use for such facts in later life. But if he failed to get acquainted with geometric proofs, he missed the best and simplest examples of true evidence and he missed the best opportunity to acquire the idea of strict reasoning. Without this idea, he lacks a true standard with which to compare alleged evidence of all sorts aimed at him in modern life.
In short, if general education intends to bestow on the student the ideas of intuitive evidence and logical reasoning, it must reserve a place for geometric proofs.
简而言之，如果普通教育打算赋予学生直观证据和逻辑推理的思想，它必须为几何证明保留一席之地。
2. Logical system. Geometry, as presented in Euclid’s Elements, is not a mere collection of facts but a logical system. The axioms, definitions, and propositions are not listed in a random sequence but disposed in accomplished order. Each proposition is so placed that it can be based on the foregoing axioms, definitions, and propositions. We may regard the disposition of the propositions as Euclid’s main achievement and their logical system as the main merit of the Elements.
2.逻辑系统。欧几里德的《元素》中提出的几何学，不是一个单纯的事实集合，而是一个逻辑系统。公理、定义和命题不是随机排列的，而是按成就的顺序排列的。每个命题都是这样被放置的，以便它可以基于前面的公理、定义和命题。我们可以把对命题的处置看作是欧几里德的主要成就，把它们的逻辑体系看作是《元素》的主要优点。
Euclid’s geometry is not only a logical system but it is the first and greatest example of such a system, which other sciences have tried, and are still trying, to imitate. Should other sciences—especially those very far from geometry, as psychology, or jurisprudence—imitate Euclid’s rigid logic? This is a debatable question; but nobody can take part in the debate with competence who is not acquainted with the Euclidean system.
欧几里德的几何学不仅是一个逻辑系统，而且是这样一个系统的第一个和最伟大的例子，其他科学已经试图，而且仍然在试图模仿。其他科学 —— 尤其是那些与几何学相去甚远的科学，如心理学或法学 —— 是否应该模仿欧几里德的僵化逻辑？这是一个值得商榷的问题；但是，没有人能够在不熟悉欧几里得体系的情况下参加辩论。
Now, the system of geometry is cemented with proofs. Each proposition is linked to the foregoing axioms, definitions, and propositions by a proof. Without understanding such proofs we cannot understand the very essence of the system.
现在，几何学的体系是用证明来巩固的。每个命题都通过一个证明与前面的公理、定义和命题相联系。如果不理解这些证明，我们就无法理解这个系统的本质。
In short, if general education intends to bestow on the student the idea of logical system, it must reserve a place for geometric proofs.
简而言之，如果普通教育打算赋予学生逻辑系统的概念，它必须为几何证明保留一个位置。
3. Mnemotechnic system. The author does not think that the ideas of intuitive evidence, strict reasoning, and logical system are superfluous for anybody. There may be cases, however, in which the study of these ideas is not considered absolutely necessary, owing to lack of time, or for other reasons. Yet even in such cases proofs may be desirable.
Proofs yield evidence; in so doing, they hold together the logical system; and they help us to remember the various items held together. Take the example discussed above, in connection with Fig. 23. This figure renders evident the fact that the sum of the angles in a triangle equals 180°. The figure connects this fact with the other fact that alternate angles are equal. Connected facts however are more interesting and are better retained than isolated facts. Thus, our figure fixes the two connected geometric propositions in our mind and, finally, the figure and the propositions may become our inalienable mental property.
证明产生了证据；这样一来，它们就把逻辑系统凝聚在一起；而且它们帮助我们记住凝聚在一起的各种项目。以上面讨论的与图 23有关的例子为例。该图表明了一个事实，即三角形中的角之和等于 180°。该图将这一事实与另一个事实联系起来，即交替的角是相等的。然而，有联系的事实比孤立的事实更有趣，也更容易被记住。因此，我们的图形将两个相连的几何命题固定在我们的头脑中，最后，图形和命题可能成为我们不可剥夺的精神财产。
Now we come to the case in which the acquisition of general ideas is not regarded as necessary, only that of certain facts is desired. Even in such a case, the facts must be presented in some connection and in some sort of system, since isolated items are laboriously acquired and easily forgotten. Any sort of connection that unites the facts simply, naturally, and durably, is welcome here. The system need not be founded on logic, it must only be designed to aid the memory effectively; it must be what is called a mnemotechnic system. Yet even from the point of view of a purely mnemotechnic system, proofs may be useful, especially simple proofs. For instance, the student must learn the fact about the sum of the angles in the triangle and that other fact about the alternate angles. Can any device to retain these facts be simpler, more natural or more effective than Fig. 23?
现在，我们来到了这样一种情况：人们不认为有必要获得一般的观念，只希望获得某些事实。即使在这种情况下，这些事实也必须以某种联系和某种系统来呈现，因为孤立的项目获得起来很费力，而且很容易忘记。在这里，任何一种能将事实简单、自然、持久地结合起来的联系都是受欢迎的。这个系统不需要建立在逻辑的基础上，它必须被设计成能够有效地帮助记忆；它必须是所谓的记忆技术系统（mnemotechnic）。然而，即使从一个纯粹的记忆技术系统的角度来看，证明可能是有用的，特别是简单的证明。例如，学生必须学习关于三角形中的角之和的事实以及关于交替角的其他事实。有什么办法能比图 23更简单、更自然或更有效地保留这些事实呢？
In short, even when no special importance is attached to general logical ideas proofs may be useful as a mnemotechnic device.
简而言之，即使在不特别重视一般逻辑思想的情况下，证明也可以作为一种记忆技术手段而发挥作用。
4. The cookbook system. We have discussed the advantages of proofs but we certainly did not advocate that all proofs should be given “in extenso.” On the contrary, there are cases in which it is scarcely possible to do so; an important case is the teaching of the differential and integral calculus to students of engineering.
If the calculus is presented according to modern standards of rigor, it demands proofs of a certain degree of difficulty and subtlety (“epsilon-proofs”). But engineers study the calculus in view of its application and have neither enough time nor enough training or interest to struggle through long proofs or to appreciate subtleties. Thus, there is a strong temptation to cut out all the proofs. Doing so, however, we reduce the calculus to the level of the cookbook.
如果微积分是按照现代的严格标准提出的，它就要求有一定程度的困难和微妙的证明（“ε-证明”）。但是，工程师研究微积分是考虑到它的应用，既没有足够的时间，也没有足够的训练或兴趣去挣扎于冗长的证明或欣赏微妙之处。因此，有一种强烈的诱惑，那就是删掉所有的证明。然而，这样做的话，我们就把微积分降低到了食谱的水平。
The cookbook gives a detailed description of ingredients and procedures but no proofs for its prescriptions or reasons for its recipes; the proof of the pudding is in the eating. The cookbook may serve its purpose perfectly. In fact, it need not have any sort of logical or mnemotechnic system since recipes are written or printed and not retained in memory.
这本食谱详细描述了成分和程序，但没有证明其处方或食谱的理由；布丁的证明就在吃的过程中。烹饪书可能完全达到了它的目的。事实上，它不需要有任何形式的逻辑或技术系统，因为菜谱是写出来或印出来的，而不是保留在记忆中。
Yet the author of a textbook of calculus, or a college instructor, can hardly serve his purpose if he follows the system of the cookbook too closely. If he teaches procedures without proofs, the unmotivated procedures are not understood. If he gives rules without reasons, the unconnected rules are quickly forgotten. Mathematics cannot be tested in exactly the same manner as a pudding; if all sorts of reasoning are debarred, a course of calculus may easily become an incoherent inventory of indigestible information.
然而，微积分教科书的作者，或大学教师，如果过于紧跟食谱的体系，就很难达到他的目的。如果他教授的程序没有证明，那么没有动机的程序就不会被理解。如果他只讲规则而不讲理由，那些没有联系的规则很快就会被遗忘。数学的测试方式不能与布丁完全相同；如果各种推理都被禁止，那么微积分课程很容易成为一个不连贯的、难以消化的信息清单。
5. Incomplete proofs. The best way of handling the dilemma between too heavy proofs and the level of the cookbook may be to make reasonable use of incomplete proofs.
5.不完整的证明。处理太重的证明和菜谱水平之间的困境的最好方法可能是合理利用不完全证明。
For a strict logician, an incomplete proof is no proof at all. And, certainly, incomplete proofs ought to be carefully distinguished from complete proofs; to confuse one with the other is bad, to sell one for the other is worse. It is painful when the author of a textbook presents an incomplete proof ambiguously, with visible hesitation between shame and the pretension that the proof is complete. But incomplete proofs may be useful when they are used in their proper place and in good taste. Their purpose is not to replace complete proofs, which they never could, but to lend interest and coherence to the presentation.
Example 1. An algebraic equation of degree n has exactly n roots. This proposition, called the Fundamental Theorem of Algebra by Gauss, must often be presented to students who are quite unprepared for understanding its proof. They know however that an equation of the first degree has one root, and one of the second degree two roots. Moreover the difficult proposition has a part that can be easily shown: no equation of degree n has more than n different roots. Do the facts mentioned constitute a complete proof for the Fundamental Theorem? By no means. They are sufficient however to lend it a certain interest and plausibility—and to fix it in the minds of the students, which is the main thing.
例 1.一个n度的代数方程 正好有n个根。这个命题被高斯称为 “代数基本定理”，必须经常向学生介绍，他们对理解其证明没有任何准备。然而，他们知道，一个一级方程式有一个根，一个二级方程式有两个根。此外，这个困难的命题也有一个容易证明的部分：n度的方程没有 多于n 个不同的根。上述事实是否构成了基本定理的完整证明？绝非如此。然而，它们足以使之具有一定的趣味性和合理性，并使之在学生的头脑中固定下来，这才是最重要的。
Example 2. The sum of any two of the plane angles formed by the edges of a trihedral angle is greater than the third. Obviously, the theorem amounts to affirming that in a spherical triangle the sum of any two sides is greater than the third. Having observed this, we naturally think of the analogy of the spherical triangle with the rectilinear triangle. Do these remarks constitute a proof? By no means; but they help us to understand and to remember the proposed theorem.
例 2.一个三面体的边所形成的平面角中，任何两个角的总和都大于第三个角。显然，该定理相当于肯定了在球面三角形中，任何两边之和都大于第三边。观察到这一点后，我们自然会想到球面三角形与直角三角形的类比。这些评论是否构成了一个证明？绝非如此；但它们有助于我们理解和记住所提出的定理。
Our first example has historical interest. For about 250 years, the mathematicians believed the Fundamental Theorem without complete proof—in fact, without much more basis than what was mentioned above. Our second example points to ANALOGY as an important source of conjectures. In mathematics, as in the natural and physical sciences, discovery often starts from observation, analogy, and induction. These means, tastefully used in framing a plausible heuristic argument, appeal particularly to the physicist and the engineer. (See also INDUCTION AND MATHEMATICAL INDUCTION, 1, 2, 3.)
The role and interest of incomplete proofs is explained to a certain extent by our study of the process of the solution. Some experience in solving problems shows that the first idea of a proof is very frequently incomplete. The most essential remark, the main connection, the germ of the proof may be there, but details must be provided afterwards and are often troublesome. Some authors, but not many, have the gift of presenting just the germ of the proof, the main idea in its simplest form, and indicating the nature of the remaining details. Such a proof, although incomplete, may be much more instructive than a proof presented with complete details.
不完整证明的作用和兴趣在一定程度上可以通过我们对解题过程的研究来解释。解决问题的一些经验表明，一个证明的第一个想法常常是不完整的。最基本的评论、主要的联系、证明的萌芽可能就在那里，但细节必须在之后提供，而且往往很麻烦。有些作者，但不是很多，有天赋只提出证明的萌芽，最简单形式的主要思想，并指出其余细节的性质。这样的证明，虽然不完整，但可能比有完整细节的证明更有启发意义。
In short, incomplete proofs may be used as a sort of mnemotechnic device (but, of course, not as substitutes for complete proofs) when the aim is tolerable coherence of presentation and not strictly logical consistency.
简而言之，当目的是可容忍的表述连贯性而不是严格的逻辑一致性时，不完全证明可以作为一种技术手段（当然，不能代替完全证明）。
It is very dangerous to advocate incomplete proofs. Possible abuse, however, may be kept within bounds by a few rules. First, if a proof is incomplete, it must be indicated as such, somewhere and somehow. Second, an author or a teacher is not entitled to present an incomplete proof for a theorem unless he knows very well a complete proof for it himself.
提倡不完整的证明是非常危险的。然而，可能的滥用可以通过一些规则控制在一定范围内。首先，如果一个证明是不完整的，它必须在某个地方以某种方式表明是如此。第二，作者或教师无权为一个定理提出不完整的证明，除非他自己非常清楚该定理的完整证明。
And it may be confessed that to present an incomplete proof in good taste is not easy at all.
而且可以承认的是，要把一个不完整的证明以良好的品味呈现出来，一点也不容易。
Some people are more and others less successful in attaining their ends and solving their problems. Such differences are noticed, discussed, and commented upon, and certain proverbs seem to have preserved the quintessence of such comments. At any rate, there are a good many proverbs which characterize strikingly the typical procedures followed in solving problems, the points of common sense involved, the usual tricks, and the usual errors. There are many shrewd and some subtle remarks in proverbs but, obviously, there is no scientific system free of inconsistencies and obscurities in them. On the contrary, many a proverb can be matched with another proverb giving exactly opposite advice, and there is a great latitude of interpretation. It would be foolish to regard proverbs as an authoritative source of universally applicable wisdom but it would be a pity to disregard the graphic description of heuristic procedures provided by proverbs.
在达到目的和解决问题方面，有些人比较成功，有些人比较不成功。这种差异被注意到，被讨论，被评论，而某些谚语似乎保留了这种评论的精髓。无论如何，有许多谚语鲜明地描述了解决问题时遵循的典型程序、涉及的常识点、通常的技巧和通常的错误。谚语中有许多精明和一些微妙的言论，但显然，在这些谚语中没有任何科学体系是不一致的和不明确的。相反，许多谚语可以与另一个谚语相匹配，给出完全相反的建议，而且有很大的解释余地。将谚语视为普遍适用的智慧的权威来源是愚蠢的，但如果无视谚语提供的启发式程序的形象描述，那就太可惜了。
It could be an interesting task to collect and group proverbs about planning, seeking means, and choosing between lines of action, in short, proverbs about solving problems. Of the space needed for such a task only a small fraction is available here; the best we can do is to quote a few proverbs illustrating the main phases of the solution emphasized in our list, and discussed in sections 6 to 14 and elsewhere. The proverbs quoted will be printed in italics.
收集和归纳关于计划、寻求手段和选择行动路线的谚语，简而言之，关于解决问题的谚语，可能是一项有趣的任务。这项工作所需的篇幅在这里只占一小部分；我们能做的就是引用一些谚语来说明我们清单中强调的解决问题的主要阶段，并在第 6 至 14 节和其他地方讨论。所引用的谚语将以斜体字印刷。
1. The very first thing we must do for our problem is to understand it: Who understands ill, answers ill. We must see clearly the end we have to attain: Think on the end before you begin. This is an old piece of advice; “respice finem” is the saying in Latin. Unfortunately, not everybody heeds such good advice, and people often start speculating, talking, and even acting fussily without having properly understood the aim for which they should work. A fool looks to the beginning, a wise man regards the end. If the end is not clear in our mind, we may easily stray from the problem and drop it. A wise man begins in the end, a fool ends in the beginning.
Yet it is not enough to understand the problem, we must also desire its solution. We have no chance to solve a difficult problem without a strong desire to solve it, but with such desire there is a chance. Where there is a will there is a way.
然而，仅仅了解问题是不够的，我们还必须渴望解决它。如果没有解决难题的强烈愿望，我们就没有机会解决这个问题，但有了这种愿望就有了机会。有意愿的地方就有办法。
2. Devising a plan, conceiving the idea of an appropriate action, is the main achievement in the solution of a problem.
2. 制定计划，构思适当的行动，是解决问题的主要成就。
A good idea is a piece of good fortune, an inspiration, a gift of the gods, and we have to deserve it: Diligence is the mother of good luck. Perseverance kills the game. An oak is not felled at one stroke. If at first you don’t succeed, try, try again. It is not enough however to try repeatedly, we must try different means, vary our trials. Try all the keys in the bunch. Arrows are made of all sorts of wood. We must adapt our trials to the circumstances. As the wind blows you must set your sail. Cut your coat according to the cloth. We must do as we may if we can’t do as we would. If we have failed, we must try something else. A wise man changes his mind, a fool never does. We should even be prepared from the outset for a possible failure of our scheme and have another one in reserve. Have two strings to your bow. We may, of course, overdo this sort of changing from one scheme to another and lose time. Then we may hear the ironical comment: Do and undo, the day is long enough. We are likely to blunder less if we do not lose sight of our aim. The end of fishing is not angling but catching.
一个好的想法是一段好运气，是一种灵感，是上天的礼物，我们必须配得上它。勤奋是好运之母。坚持不懈的努力会杀死游戏。橡树是不会被一刀砍倒的。如果一开始你没有成功，那就试试，再试试。然而，光是反复尝试是不够的，我们必须尝试不同的方法，改变我们的试验。试试这串钥匙中的所有钥匙。箭是由各种木材制成的。我们必须使我们的试验适应环境。风怎么吹，你就必须扬起你的帆。衣服要根据布来剪。如果我们不能如愿以偿，我们就必须尽力而为。如果我们失败了，我们必须尝试别的东西。聪明人会改变主意，傻瓜永远不会改变。我们甚至应该从一开始就为我们的计划可能失败做好准备，并储备另一个计划。弓上要有两根弦。当然，我们可能会过度追求这种从一个计划到另一个计划的变化，从而失去时间。然后我们可能会听到讽刺的评论。做和不做，一天已经够长了。如果我们不忽视我们的目标，我们就有可能减少失误。钓鱼的目的不是垂钓而是捕鱼。
We work hard to extract something helpful from our memory, yet, quite often, when an idea that could be helpful presents itself, we do not appreciate it, for it is so inconspicuous. The expert has, perhaps, no more ideas than the inexperienced, but appreciates more what he has and uses it better. A wise man will make more opportunities than he finds. A wise man will make tools of what comes to hand. A wise man turns chance into good fortune. Or, possibly, the advantage of the expert is that he is continually on the lookout for opportunities. Have an eye to the main chance.
3. We should start carrying out our plan at the right moment, when it is ripe, but not before. We should not start rashly. Look before you leap. Try before you trust. A wise delay makes the road safe. On the other hand, we should not hesitate too long. If you will sail without danger you must never put to sea. Do the likeliest and hope the best. Use the means and God will give the blessing.
3. 我们应该在适当的时候开始执行我们的计划，当它成熟的时候，但不是之前。我们不应轻率地开始。在跃进之前先看看。先试后信。明智的延迟使道路安全。另一方面，我们也不应该犹豫太长时间。如果你想在没有危险的情况下航行，你必须永远不要出海。做最可能的，希望最好的。使用手段，上帝会赐予祝福。
We must use our judgment to determine the right moment. And here is a timely warning that points out the most common fallacy, the most usual failure of our judgment: We soon believe what we desire.
我们必须用我们的判断力来确定正确的时机。这里有一个及时的警告，指出了最常见的谬误，我们判断力最常见的失败。我们很快就会相信我们所希望的。
Our plan gives usually but a general outline. We have to convince ourselves that the details fit into the outline, and so we have to examine carefully each detail, one after the other. Step after step the ladder is ascended. Little by little as the cat ate the flickle. Do it by degrees.
我们的计划通常只是一个总纲。我们必须说服自己，使细节符合纲要，因此我们必须一个接一个地仔细检查每个细节。梯子一步又一步地往上爬。渐渐地，就像猫吃了弹子一样。循序渐进地做。
In carrying out our plan we must be careful to arrange its steps in the proper order, which is frequently just the reverse of the order of invention. What a fool does at last, a wise man does at first.
在执行我们的计划时，我们必须小心翼翼地按照适当的顺序安排其步骤，而这往往与发明的顺序正好相反。愚蠢的人最后做的事，聪明的人一开始就做了。
4. Looking back at the completed solution is an important and instructive phase of the work. He thinks not well that thinks not again. Second thoughts are best.
4. 回顾已完成的解决方案是工作的一个重要和指导性的阶段。他想得不好那就不要再想了。第二次思考是最好的。
5. We have by no means exhausted the comments of proverbs on the solution of problems. Yet many other proverbs which could be quoted would scarcely furnish new themes, only variations on the themes already mentioned. Certain more systematic and more sophisticated aspects of the process of solution are hardly within the scope of the Wisdom of Proverbs.
5. 我们绝没有穷尽谚语中关于解决问题的评论。然而，许多其他可以引用的谚语几乎没有提供新的主题，只是在已经提到的主题上有所变化。在解决问题的过程中，某些更系统、更复杂的方面几乎不在《智慧箴言》的范围之内。
In describing the more systematic aspects of the solution, the author tried now and then to imitate the peculiar turn of proverbs, which is not easy. Here follow a few “synthetic” proverbs which describe somewhat more sophisticated attitudes.
在描述解决方案的更系统方面，作者不时尝试模仿谚语的奇特转折，这并不容易。下面是几个 “合成” 的谚语，它们描述的态度有些复杂。
The end suggests the means.
目的表明手段。
Your five best friends are What, Why, Where, When, and How. You ask What, you ask Why, you ask Where, When, and How—and ask nobody else when you need advice.
你的五个最好的朋友是 “什么”、“为什么”、“哪里”、“何时” 和 “如何”。你要问什么，你要问为什么，你要问哪里，什么时候，怎么做 —— 当你需要建议时，不要问其他人。
Do not believe anything but doubt only what is worth doubting.
不要相信任何东西，只怀疑值得怀疑的东西。
Look around when you have got your first mushroom or made your first discovery; they grow in clusters.
当你得到你的第一个蘑菇或有了第一个发现时，看看周围；它们是成群结队地生长的。
Working backwards. If we wish to understand human behavior we should compare it with animal behavior. Animals also “have problems” and “solve problems.” Experimental psychology has made essential progress in the last decades in exploring the “problem-solving” activities of various animals. We cannot discuss here these investigations but we shall describe sketchily just one simple and instructive experiment and our description will serve as a sort of comment upon the method of analysis, or method of “working backwards.” This method, by the way, is discussed also elsewhere in the present book, under the name of PAPPUS to whom we owe an important description of the method.
1. Let us try to find an answer to the following tricky question: How can you bring up from the river exactly six quarts of water when you have only two containers, a four quart pail and a nine quart pail, to measure with?
1. 让我们试着为下面这个棘手的问题找一个答案。当你只有两个容器，一个四夸脱的桶和一个九夸脱的桶来测量时，你怎么能从河里带出正好六夸脱的水？
Let us visualize clearly the given tools we have to work with, the two containers. (What is given?) We imagine two cylindrical containers having equal bases whose altitudes are as 9 to 4, see Fig. 24. If along the lateral surface of each container there were a scale of equally spaced horizontal lines from which we could tell the height of the waterline, our problem would be easy. Yet there is no such scale and so we are still far from the solution.
让我们清楚地想象一下我们所要使用的工具，即两个容器。（给定的是什么？）我们想象两个圆柱形的容器，其底面相等，高度为 9 到 4，见图 24。如果沿着每个容器的侧面有一个等距水平线的标尺，我们可以从中看出水线的高度，那么我们的问题就容易了。但是没有这样的标尺，所以我们离解决方案还很远。
FIG. 24
图 24
We do not know yet how to measure exactly 6 quarts; but could we measure something else? (If you cannot solve the proposed problem try to solve first some related problem. Could you derive something useful from the data?) Let us do something, let us play around a little. We could fill the larger container to full capacity and empty so much as we can into the smaller container; then we could get 5 quarts. Could we also get 6 quarts? Here are again the two empty containers. We could also . . .
我们还不知道如何精确地测量 6 夸脱；但我们可以测量其他东西吗？（如果你不能解决所提出的问题，请先解决一些相关问题。你能从这些数据中得出一些有用的东西吗？）让我们做一些事情，让我们玩一玩。我们可以把较大的容器装满，然后把尽可能多的东西倒入较小的容器；那么我们可以得到 5 夸脱。我们还能得到 6 夸脱吗？这里又是两个空容器。我们还可以……
We are working now as most people do when confronted with this puzzle. We start with the two empty containers, we try this and that, we empty and fill, and when we do not succeed, we start again, trying something else. We are working forwards, from the given initial situation to the desired final situation, from the data to the unknown. We may succeed, after many trials, accidentally.
2. But exceptionally able people, or people who had the chance to learn in their mathematics classes something more than mere routine operations, do not spend too much time in such trials but turn around, and start working backwards.
2. 但特别能干的人，或者有机会在数学课上学到比单纯的常规操作更多的东西的人，不会在这种试验中花费太多时间，而是转过身来，开始向后工作。
What are we required to do? (What is the unknown?) Let us visualize the final situation we aim at as clearly as possible. Let us imagine that we have here, before us, the larger container with exactly 6 quarts in it and the smaller container empty as in Fig. 25. (Let us start from what is required and assume what is sought as already found, says Pappus.)
我们需要做什么？（未知数是什么？）让我们尽可能清楚地想象一下我们所要的最终情况。让我们想象一下，我们面前有一个大容器，里面正好有 6 夸脱，小容器是空的，如图 25所示。（帕普斯说：“让我们从所需的东西开始，并假设所寻求的东西已经找到。）
FIG. 25
图 25
From what foregoing situation could we obtain the desired final situation shown in Fig. 25? (Let us inquire from what antecedent the desired result could be derived, says Pappus.) We could, of course, fill the larger container to full capacity, that is, to 9 quarts. But then we should be able to pour out exactly three quarts. To do that . . . we must have just one quart in the smaller container! That’s the idea. See Fig. 26.
(The step that we have just completed is not easy at all. Few persons are able to take it without much foregoing hesitation. In fact, recognizing the significance of this step, we foresee an outline of the following solution.)
（我们刚刚完成的这一步一点也不容易。很少有人能在没有太多的前述犹豫的情况下迈出这一步。事实上，认识到这一步的重要性，我们预见了以下解决方案的轮廓）。
FIG. 26
图 26
But how can we reach the situation that we have just found and illustrated by Fig. 26? (Let us inquire again what could be the antecedent of that antecedent.) Since the amount of water in the river is, for our purpose, unlimited, the situation of Fig. 26 amounts to the same as the next one in Fig. 27
FIG. 27
图 27
It is easy to recognize that if any one of the situations in Figs. 26, 27, 28 is obtained, any other can be obtained just as well, but it is not so easy to hit upon Fig. 28, unless we have seen it before, encountered it accidentally in one of our initial trials. Playing around with the two containers, we may have done something similar and remember now, in the right moment, that the situation of Fig. 28 can arise as suggested by Fig. 29: We fill the large container to full capacity, and pour from it four quarts into the smaller container and then into the river, twice in succession. We came eventually upon something already known (these are Pappus’s words) and following the method of analysis, working backwards, we have discovered the appropriate sequence of operations.
FIG. 29
图 29
It is true, we have discovered the appropriate sequence in retrogressive order but all that is left to do is to reverse the process and start from the point which we reached last of all in the analysis (as Pappus says). First, we perform the operations suggested by Fig. 29 and obtain Fig. 28; then we pass to Fig. 27, then to Fig. 26, and finally to Fig. 25. Retracing our steps, we finally succeed in deriving what was required.
3. Greek tradition attributed to Plato the discovery of the method of analysis. The tradition may not be quite reliable but, at any rate, if the method was not invented by Plato, some Greek scholar found it necessary to attribute its invention to a philosophical genius.
3. 希腊传统将分析方法的发现归于柏拉图。这个传统可能不太可靠，但无论如何，如果这个方法不是柏拉图发明的，一些希腊学者认为有必要把它的发明归于一个哲学天才。
There is certainly something in the method that is not superficial. There is a certain psychological difficulty in turning around, in going away from the goal, in working backwards, in not following the direct path to the desired end. When we discover the sequence of appropriate operations, our mind has to proceed in an order which is exactly the reverse of the actual performance. There is some sort of psychological repugnance to this reverse order which may prevent a quite able student from understanding the method if it is not presented carefully.
在这个方法中，当然有一些不是表面的东西。掉头、远离目标、倒退、不沿着直接的路径到达预期的目的，这在心理上有一定的困难。当我们发现适当操作的顺序时，我们的思想必须按照与实际操作完全相反的顺序进行。对这种相反的顺序有某种心理上的厌恶，如果不仔细介绍，可能会妨碍一个相当有能力的学生理解这种方法。
Yet it does not take a genius to solve a concrete problem working backwards; anybody can do it with a little common sense. We concentrate upon the desired end, we visualize the final position in which we would like to be. From what foregoing position could we get there? It is natural to ask this question, and in so asking we work backwards. Quite primitive problems may lead naturally to working backwards; see PAPPUS, 4.
然而，要解决一个具体的问题，并不需要一个天才，只要有一点常识，任何人都可以做到这一点。我们把注意力集中在所期望的目标上，我们设想我们希望达到的最终位置。我们能从哪个位置到达那里？问这个问题是很自然的，而在问的过程中，我们会向后努力。相当原始的问题可能会自然地导致倒退；见《PAPPUS》，4。
Working backwards is a common-sense procedure within the reach of everybody and we can hardly doubt that it was practiced by mathematicians and nonmathematicians before Plato. What some Greek scholar may have regarded as an achievement worthy of the genius of Plato is to state the procedure in general terms and to stamp it as an operation typically useful in solving mathematical and nonmathematical problems.
4. And now, we turn to the psychological experiment—if the transition from Plato to dogs, hens, and chimpanzees is not too abrupt. A fence forms three sides of a rectangle but leaves open the fourth side as shown in Fig. 30. We place a dog on one side of the fence, at the point D, and some food on the other side, at the point F. The problem is fairly easy for the dog. He may first strike a posture as if to spring directly at the food but then he quickly turns about, dashes off around the end of the fence and, running without hesitation, reaches the food in a smooth curve. Sometimes, however, especially when the points D and F are close to each other, the solution is not so smooth; the dog may lose some time in barking, scratching, or jumping against the fence before he “conceives the bright idea” (as we would say) of going around.
4. 现在，我们转向心理学实验 —— 如果从柏拉图到狗、母鸡和黑猩猩的过渡不是太突然的话。如图 30所示，一个篱笆构成了一个长方形的三条边，但第四条边是开放的。我们把一只狗放在栅栏的一边，即D点，把一些食物放在另一边，即F点。它先是摆出一副要直接扑向食物的姿态，然后迅速转身，绕过栅栏的一端，毫不犹豫地跑向食物，以一个平稳的曲线到达食物。然而，有时，特别是当D点和F点相互靠近时，解决办法就不那么顺利了；狗可能会在吠叫、抓挠或跳到栅栏上的过程中耽误一些时间，然后它才 “想出一个聪明的主意”（正如我们所说的）绕过去。
FIG. 30
图 30
It is interesting to compare the behavior of various animals put into the place of the dog. The problem is very easy for a chimpanzee or a four-year-old child (for whom a toy may be a more attractive lure than food). The problem, however, turns out to be surprisingly difficult for a hen who runs back and forth excitedly on her side of the fence and may spend considerable time before getting at the food if she gets there at all. But she may succeed, after much running, accidentally.
5. We should not build a big theory upon just one simple experiment which was only sketchily reported. Yet there can be no disadvantage in noticing obvious analogies provided that we are prepared to recheck and revalue them.
5. 我们不应该仅仅在一个简单的实验上建立一个大的理论，而这个实验只是粗略的报告。然而，只要我们准备好重新检查和评估，注意到明显的类比就不会有什么坏处。
Going around an obstacle is what we do in solving any kind of problem; the experiment has a sort of symbolic value. The hen acted like people who solve their problem muddling through, trying again and again, and succeeding eventually by some lucky accident without much insight into the reasons for their success. The dog who scratched and jumped and barked before turning around solved his problem about as well as we did ours about the two containers. Imagining a scale that shows the waterline in our containers was a sort of almost useless scratching, showing only that what we seek lies deeper under the surface. We also tried to work forwards first, and came to the idea of turning round afterwards. The dog who, after brief inspection of the situation, turned round and dashed off gives, rightly or wrongly, the impression of superior insight.
绕过障碍物是我们在解决任何一种问题时的做法；这个实验具有某种象征性的价值。这只母鸡的行为就像人们在解决他们的问题时得过且过，一次又一次地尝试，最终因某种幸运的意外而成功，但对他们成功的原因却没有太多的了解。这只狗在转身之前又抓又跳又叫，它解决了自己的问题，就像我们解决两个容器的问题一样。想象一个显示我们容器中水线的刻度是一种几乎无用的抓挠，只表明我们所寻求的东西在表面之下更深。我们还试图先向前工作，并在事后产生了转身的想法。那只狗在简单检查了情况后，转身就走，不管是对是错，都给人留下了洞察力超群的印象。
No, we should not even blame the hen for her clumsiness. There is a certain difficulty in turning round, in going away from the goal, in proceeding without looking continually at the aim, in not following the direct path to the desired end. There is an obvious analogy between her difficulties and our difficulties.
不，我们甚至不应该为母鸡的笨拙而责备它。在转弯时，在远离目标时，在没有持续关注目标的情况下继续前进时，在没有沿着直接的路径到达预期的目的时，都有一定的困难。她的困难和我们的困难之间有一个明显的相似之处。
1 The text is slightly rearranged. For a more exact translation see William Whewell, The Philosophy of the Inductive Sciences (1847), vol. II, p. 131.
1文中略作了重新安排。更准确的翻译见威廉·惠韦尔，《归纳科学的哲学》（1847），第二卷，第 131 页。
2 The plane is bisected by the line through B and C. We choose one of the halfplanes to construct A in it, and so we may consider just one parallel to BC; otherwise, we should consider two such parallels.
2该平面被通过B和C的直线一分为二。我们选择其中一个半平面，在其中构建A，因此我们可以只考虑一条与BC的平行线；否则，我们应该考虑两条这样的平行线。
3 In this respect, ideas have changed since the time of Euclid and his Greek followers who defined the point, the straight line, and the plane. Their “definitions” however are scarcely formal definitions, rather intuitive illustrations of a sort. Illustrations, of course, are allowed, and even very desirable in teaching.
3在这方面，自从欧几里德和他的希腊追随者定义了点、直线和平面后，思想已经发生了变化。然而，他们的 “定义” 几乎不是正式的定义，而是某种直觉上的说明。当然，插图是允许的，甚至在教学中也是非常可取的。
5 If the angles of a triangle are α, β, γ and 90° > α > β > γ, then at least one of the differences 90° − α, α − β, β − γ is < 15°, unless α = 75°, β = 60°, γ = 45°. In fact,
5如果一个三角形的角是α，β，γ和 90°>α>β>γ，那么 90°-α，α-β，β-γ中至少有一个差异<15°，除非α=75°，β=60°，γ=45°。事实上。
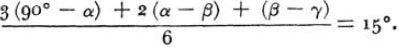
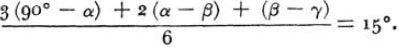
6 See also a paper by the author in American Mathematical Monthly, vol. 48, pp. 450-465.
6另见作者在《美国数学月刊》上的一篇论文，第 48 卷，第 450-465 页。
7 T. L. Heath, The Thirteen Books of Euclid’s Elements, Cambridge, 1908, vol. 1, p. 138.
7T·L. Heath,The Thirteen Books of Euclid's Elements, Cambridge, 1908, vol. 1, p. 138。
8 Several points discussed in this article are more fully considered in the author’s paper, Acta Psychologica, vol. 4 (1938), pp. 113-170.
8本文讨论的几个问题在作者的论文中得到了更充分的考虑，Acta Psychologica，第 4 卷（1938），第 113-170 页。
9 The American Mathematical Monthly, vol. 50 (1943), p. 124 and vol. 51 (1944), pp. 234-236.
9美国数学月刊》，第 50 卷（1943 年），第 124 页和第 51 卷（1944 年），第 234-236 页。
This last part offers the reader additional opportunity for practice.
这最后一部分为读者提供了额外的练习机会。
The problems require no more preliminary knowledge than the reader could have acquired from a good high-school curriculum. Yet they are not too easy and not mere routine problems; some of them demand originality and ingenuity.12
这些问题要求的初步知识并不比读者从良好的高中课程中获得的更多。然而，这些问题并不容易，也不仅仅是常规问题；其中一些问题需要原创性和独创性。12
The hints offer indications leading to the result, mostly by quoting an appropriate sentence from the list; to a very attentive reader ready to pick up suggestions they may reveal the key idea of the solution.
这些提示提供了通往结果的指示，主要是通过引用列表中适当的句子；对于非常细心的读者来说，他们可能揭示了解决方案的关键思想。
The solutions bring not only the answer but also the procedure leading to the answer, although, of course, the reader has to supply some of the details. Some solutions try to open up some further outlook by a few words placed at the end.
这些解决方案不仅带来了答案，还带来了导致答案的程序，当然，读者必须提供一些细节。一些解决方案试图通过在结尾处的几句话来打开一些进一步的前景。
The reader who has earnestly tried to solve the problem has the best chance to profit by the hint and the solution. If he obtains the result by his own means, he may learn something by comparing his method with the method given in print. If, after a serious effort, he is inclined to give up, the hint may supply him with the missing idea. If even the hint does not help, he may look at the solution, try to isolate the key idea, put the book aside, and then try to work out the solution.
1. A bear, starting from the point P, walked one mile due south. Then he changed direction and walked one mile due east. Then he turned again to the left and walked one mile due north, and arrived exactly at the point P he started from. What was the color of the bear?
1. 一只熊，从P点开始，向正南方向走了一英里。然后他改变方向，向东走了一英里。然后他又向左转，向正北走了一英里，正好到达了他出发的P点。这只熊的颜色是什么？
2. Bob wants a piece of land, exactly level, which has four boundary lines. Two boundary lines run exactly north-south, the two others exactly east-west, and each boundary line measures exactly 100 feet. Can Bob buy such a piece of land in the U.S.?
2. 鲍勃想要一块土地，完全平整，有四条边界线。两条边界线正好是南北走向，另外两条正好是东西走向，每条边界线正好 100 英尺。鲍勃能在美国买到这样一块土地吗？
3. Bob has 10 pockets and 44 silver dollars. He wants to put his dollars into his pockets so distributed that each pocket contains a different number of dollars. Can he do so?
3. 鲍勃有 10 个口袋和 44 块银元。他想把美元放进口袋，使每个口袋都有不同数量的美元。他能这样做吗？
4. To number the pages of a bulky volume, the printer used 2989 digits. How many pages has the volume?
4. 为了给一卷庞大的书编号，打印机使用了 2989 位数字。该卷有多少页？
5. Among Grandfather’s papers a bill was found:
5. 在祖父的文件中发现了一张账单。
The first and last digit of the number that obviously represented the total price of those fowls are replaced here by blanks, for they have faded and are now illegible.
显然代表这些鸡的总价格的数字的第一个和最后一个数字在这里被空白所取代，因为它们已经褪色，现在无法辨认。
What are the two faded digits and what was the price of one turkey?
两个褪色的数字是什么，一只火鸡的价格是多少？
6. Given a regular hexagon and a point in its plane. Draw a straight line through the given point that divides the given hexagon into two parts of equal area.
6. 给出一个正六边形和其平面上的一个点。通过给定的点画一条直线，将给定的六边形分成面积相等的两部分。
7. Given a square. Find the locus of the points from which the square is seen under an angle (a) of 90° (b) of 45°. (Let P be a point outside the square, but in the same plane. The smallest angle with vertex P containing the square is the “angle under which the square is seen” from P.) Sketch clearly both loci and give a full description.
8. Call “axis” of a solid a straight line joining two points of the surface of the solid and such that the solid, rotated about this line through an angle which is greater than 0° and less than 360° coincides with itself.
8. 将实体的 “轴” 称为连接该实体表面两点的直线，并使该实体围绕该直线旋转一个大于 0°且小于 360°的角度时与自身重合。
Find the axes of a cube. Describe clearly the location of the axes, find the angle of rotation associated with each. Assuming that the edge of the cube is of unit length, compute the arithmetic mean of the lengths of the axes.
找到一个立方体的轴。清楚地描述各轴的位置，找出与各轴相关的旋转角度。假设立方体的边缘为单位长度，计算各轴长度的算术平均值。
9. In a tetrahedron (which is not necessarily regular) two opposite edges have the same length a and they are perpendicular to each other. Moreover they are each perpendicular to a line of length b which joins their midpoints. Express the volume of the tetrahedron in terms of a and b, and prove your answer.
9. 在一个四面体（不一定是规则的）中，两条相对的边有相同的长度a，它们相互垂直。此外，它们都垂直于连接其中点的长度为b的线。用a和b来表示四面体的体积，并证明你的答案。
10. The vertex of a pyramid opposite the base is called the apex. (a) Let us call a pyramid “isosceles” if its apex is at the same distance from all vertices of the base. Adopting this definition, prove that the base of an isosceles pyramid is inscribed in a circle the center of which is the foot of the pyramid’s altitude.
10. 金字塔中与底面相对的顶点被称为顶点。（a）如果一个金字塔的顶点与底面的所有顶点距离相同，我们就称其为 “等腰三角形”。采用这个定义，证明等腰三角形金字塔的底面被刻在一个圆内，该圆的中心是金字塔的高度的脚。
(b) Now let us call a pyramid “isosceles” if its apex is at the same (perpendicular) distance from all sides of the base. Adopting this definition (different from the foregoing) prove that the base of an isosceles pyramid is circumscribed about a circle the center of which is the foot of the pyramid’s altitude.
（b）现在让我们称一个金字塔为 “等腰三角形”，如果它的顶点与底座的所有边都在同一（垂直）距离。采用这个定义（与前述不同），证明等腰三角形金字塔的底面是围绕一个圆的，该圆的中心是金字塔的高度脚。
11. Find x, y, u, and v, satisfying the system of four equations
11. 找出x、y、u和v，满足四项方程的系统
(This may look long and boring: look for a short cut.)
（这可能看起来很长，很无聊：寻找一条捷径）。
12. Bob, Peter, and Paul travel together. Peter and Paul are good hikers; each walk p miles per hour. Bob has a bad foot and drives a small car in which two people can ride, but not three; the car covers c miles per hour. The three friends adopted the following scheme: They start together, Paul rides in the car with Bob, Peter walks. After a while, Bob drops Paul, who walks on; Bob returns to pick up Peter, and then Bob and Peter ride in the car till they overtake Paul. At this point they change: Paul rides and Peter walks just as they started and the whole procedure is repeated as often as necessary.
12. 鲍勃、彼得和保罗一起旅行。彼得和保罗都是徒步旅行的好手；每人每小时走p英里。鲍勃的脚不好，开的是一辆小车，可以坐两个人，但不能坐三个人；这辆车每小时能走c英里。这三个朋友采用了以下方案。他们一起出发，保罗和鲍勃一起坐车，彼得走路。过了一会儿，鲍勃把保罗放下，他继续走；鲍勃回来接彼得，然后鲍勃和彼得坐车，直到他们超过保罗。在这一点上，他们改变了。保罗骑车，彼得走路，就像他们开始时一样，整个过程在必要时重复。
(a) How much progress (how many miles) does the company make per hour?
（a）公司每小时能取得多少进展（多少英里）？
(b) Through which fraction of the travel time does the car carry just one man?
（b）在哪一部分的旅行时间里，汽车只载一个人？
(c) Check the extreme cases p = 0 and p = c.
（c）检查极端情况p=0 和p=c。
13. Three numbers are in arithmetic progression, three other numbers in geometric progression. Adding the corresponding terms of these two progressions successively, we obtain
13. 三个数字是算术级数，另外三个数字是几何级数。将这两个级数的相应项依次相加，我们可以得到
respectively, and, adding all three terms of the arithmetic progression, we obtain 126. Find the terms of both progressions.
分别，将算术级数的所有三个项相加，我们得到 126。找出这两个进阶的项。
14. Determine m so that the equation in x
14. 确定m，使x中的方程
has four real roots in arithmetic progression.
有四个实数根的算术级数。
16. From the peak of a mountain you see two points, A and B, in the plain. The lines of vision, directed to these points, include the angle γ. The inclination of the first line of vision to a horizontal plane is α, that of the second line β. It is known that the points A and B are on the same level and that the distance between them is c.
16. 从山顶上看到平原上的两个点，A和B。第一条视线对水平面的倾斜度为α，第二条视线的倾斜度为β，已知A、B两点在同一水平面上，它们之间的距离为c。
Express the elevation x of the peak above the common level of A and B in terms of the angles α, β, γ, and the distance c.
用角度α、β、γ和距离c来表示山峰在A和B的共同水平面以上的标高x。
17. Observe that the value of
17. 观察到的值是
is 1/2, 5/6, 23/24 for n = 1,2,3, respectively, guess the general law (by observing more values if necessary) and prove your guess.
n=1,2,3 时分别为 1/2,5/6,23/24，猜测一般规律（必要时观察更多的数值）并证明你的猜测。
18. Consider the table
18. 请考虑以下表格
Guess the general law suggested by these examples, express it in suitable mathematical notation, and prove it.
猜测这些例子所暗示的一般规律，用合适的数学符号表达，并证明它。
19. The side of a regular hexagon is of length n (n is an integer). By equidistant parallels to its sides the hexagon is divided into T equilateral triangles each of which has sides of length 1. Let V denote the number of vertices appearing in this division, and L the number of boundary lines of length 1. (A boundary line belongs to one or two triangles, a vertex to two or more triangles.) When n = 1, which is the simplest case, T = 6, V = 7, L = 12. Consider the general case and express T, V, and L in terms of n. (Guessing is good, proving is better.)
20. In how many ways can you change one dollar? (The “way of changing” is determined if it is known how many coins of each kind—cents, nickels, dimes, quarters, half dollars—are used.)
20. 你可以用多少种方式换取一美元？（如果知道每种硬币的数量 —— 美分、五分、一角、二角、半美元 —— 就可以确定 “换取的方式”）。
1. What is the unknown? The color of a bear—but how could we find the color of a bear from mathematical data? What is given? A geometrical situation—but it seems self-contradictory: how could the bear, after walking three miles in the manner described, return to his starting point?
1.未知数是什么？熊的颜色 —— 但我们如何能从数学数据中找到熊的颜色？给定的是什么？一个几何情况 —— 但它似乎是自相矛盾的：熊以所述方式走了三英里后，怎么可能回到他的出发点？
2. Do you know a related problem?
2.你知道一个相关的问题吗？
3. If Bob had very many dollars, he would have obviously no difficulty in filling each of his pockets differently. Could you restate the problem? What is the minimum number of dollars that can be put in 10 pockets so that no two different pockets contain the same amount?
3. 如果鲍勃有非常多的美元，他显然不难以不同的方式填满他的每个口袋。你能重述一下这个问题吗？在 10 个口袋里最少可以装多少美元，才能使两个不同的口袋里没有相同的钱？
4. Here is a problem related to yours: If the book has exactly 9 numbered pages, how many digits uses the printer? (9, of course.) Here is another problem related to yours: If the book has exactly 99 numbered pages, how many digits does the printer use?
4.这里有一个与你有关的问题。如果这本书正好有 9 个编号的页面，那么打印机使用多少个数字？（当然是 9。）下面是另一个与你有关的问题。如果这本书正好有 99 页编号，那么打印机使用多少位数字？
5. Could you restate the problem? What can the two faded digits be if the total price, expressed in cents, is divisible by 72?
5.你能重述一下这个问题吗？如果以美分为单位的总价能被 72 整除，那么这两个消逝的数字可以是什么？
6. Could you imagine a more accessible related problem? A more general problem? An analogous problem? (GENERALIZATION, 2.)
6.你能想象一个更容易获得的相关问题吗？一个更普遍的问题？一个类似的问题？（一般化，2.）
8. I assume that the reader is familiar with the shape of the cube and has found certain axes just by inspection—but are they all the axes? Can you prove that your list of axes is exhaustive? Has your list a clear principle of classification?
8. 我假设读者对立方体的形状很熟悉，并且仅仅通过检查就发现了某些轴 —— 但它们是所有的轴吗？你能证明你列出的轴是详尽的吗？你的清单有明确的分类原则吗？
9. Look at the unknown! The unknown is the volume of a tetrahedron—yes, I know, the volume of any pyramid can be computed when the base and the height are given (product of both, divided by 3) but in the present case neither the base nor the height is given. Could you imagine a more accessible related problem? (Don’t you see a more accessible tetrahedron which is an aliquot part of the given one?)
9.看看这个未知数吧!未知数是四面体的体积 —— 是的，我知道，任何金字塔的体积都可以在给出底和高的情况下计算出来（两者的乘积，除以 3），但在本例中，底和高都没有给出。你能想象一个更容易理解的相关问题吗？（难道你没有看到一个更容易获得的四面体，它是给定的四面体的一个部分吗？）
10. Do you know a related theorem? Do you know a related . . . simpler . . . analogous theorem? Yes: the foot of the altitude is the mid-point of the base in an isosceles triangle. Here is a theorem related to yours and proved before. Could you use . . . its method? The theorem on the isosceles triangle is proved from congruent right triangles of which the altitude is a common side.
10.你知道一个相关的定理吗？你知道一个相关的…… 更简单的…… 类似的定理吗？是的：在一个等腰三角形中，高度的脚是底面的中点。这里有一个与你有关的定理，以前也证明过。你能用…… 它的方法 吗 ？关于等腰三角形的定理是由全等的直角三角形证明的，其中高度是一个公共边。
11. It is assumed that the reader is somewhat familiar with systems of linear equations. To solve such a system, we have to combine its equations in some way—look out for relations between the equations which could indicate a particularly advantageous combination.
11. 我们假设读者对线性方程组有一定的了解。为了解决这样一个系统，我们必须以某种方式组合其方程 —— 寻找方程之间的关系，这可能表明一个特别有利的组合。
12. Separate the various parts of the condition. Can you write them down? Between the start and the point where the three friends meet again there are three different phases:
12.把条件的各个部分分开。你能把它们写下来吗？从开始到三个朋友再次相遇，有三个不同的阶段。
(1) Bob rides with Paul
(2) Bob rides alone
(3) Bob rides with Peter.
（1）鲍勃和保罗一起骑车
（2）鲍勃单独骑车
（3）鲍勃和彼得一起骑车。
13. Separate the various parts of the condition. Can you write them down? Let
13.把条件的各个部分分开。你能把它们写下来吗？让
be the terms of the arithmetic progression, and
是算术级数的项，和
be the terms of the geometric progression.
是几何级数的条款。
14. What is the condition? The four roots must form an arithmetic progression. Yet the equation has a particular feature: it contains only even powers of the unknown x. Therefore, if a is a root, −a is also a root.
14.这个条件是什么？四个根必须构成一个算术级数。然而，这个方程有一个特点：它只包含未知数x的偶数次方。
15. Separate the various parts of the condition. Can you write them down? We may distinguish three parts in the condition, concerning
15.把条件的各个部分分开。你能把它们写下来吗？我们可以区分条件中的三个部分，涉及
(1) perimeter
(2) right triangle
(3) height to hypotenuse.
（1）周长
（2）直角三角形
（3）高度与斜边的关系。
16. Separate the various parts of the condition. Can you write them down? Let a and b stand for the lengths of the (unknown) lines of vision, α and β for their inclinations to the horizontal plane, respectively. We may distinguish three parts in the condition, concerning
16.把条件的各个部分分开。你能把它们写下来吗？让a和b代表（未知）视线的长度，α和β分别代表它们对水平面的倾斜度。我们可以区分条件中的三个部分，分别是
(1) the inclination of a
(2) the inclination of b
(3) the triangle with sides a, b, and c.
（1）a的倾斜度
（2）b的倾斜度
（3）边为a、b、c的三角形。
17. Do you recognize the denominators 2, 6, 24? Do you know a related problem? An analogous problem? (INDUCTION AND MATHEMATICAL INDUCTION.)
17. 你认识分母 2、6、24 吗？你知道一个相关的问题吗？一个类似的问题？（归纳法和数学归纳法）。
19. Draw a figure. Its observation may help you to discover the law inductively, or it may lead you to relations between T, V, L, and n.
19.画一个图。对它的观察可能有助于你归纳发现规律，也可能引导你发现T、V、L和n之间的关系。
20. What is the unknown? What are we supposed to seek? Even the aim of the problem may need some clarification. Could you imagine a more accessible related problem? A more general problem? An analogous problem? Here is a very simple analogous problem: In how many ways can you pay one cent? (There is just one way.) Here is a more general problem: In how many ways can you pay the amount of n cents using these five kinds of coins: cents, nickels, dimes, quarters, and half dollars. We are especially concerned with the particular case n = 100.
20.未知是什么？我们应该寻求什么？甚至问题的目的也可能需要澄清一下。你能想象一个更容易理解的相关问题吗？一个更普遍的问题？一个类似的问题？这里有一个非常简单的类似问题：你可以用多少种方式支付 1 美分？（只有一种方法。）这里有一个更普遍的问题：用这五种硬币：美分、五分、一角、二角和半元，你可以用多少种方法支付n美分的金额。我们特别关注n=100 这种特殊情况。
In the simplest particular cases, for small n, we can figure out the answer without any high-brow method, just by trying, by inspection. Here is a short table (which the reader should check).
在最简单的特殊情况下，对于小的n，我们不需要任何高深的方法，只要通过尝试，通过检查，就可以找出答案。这里有一个简短的表格（读者应该检查）。
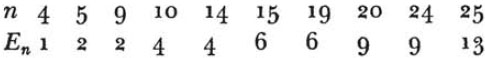
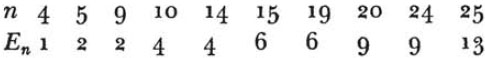
The first line lists the amounts to be paid, generally called n. The second line lists the corresponding numbers of “ways of paying,” generally called En. (Why I have chosen this notation is a secret of mine which I am not willing to give away at this stage.)
第一行列出要支付的金额，一般称为n。第二行列出相应数量的 “支付方式”，一般称为En。（为什么我选择这种记法是我的一个秘密，在这个阶段我不愿意透露）。
We are especially concerned with E100, but there is little hope that we can compute E100 without some clear method. In fact the present problem requires a little more from the reader than the foregoing ones; he should create a little theory.
我们特别关注E100，但如果没有一些明确的方法，我们计算E100的希望很小。事实上，目前的问题对读者的要求比前面的问题多一点；他应该创造一点理论。
1. You think that the bear was white and the point P is the North Pole? Can you prove that this is correct? As it was more or less understood, we idealize the question. We regard the globe as exactly spherical and the bear as a moving material point. This point, moving due south or due north, describes an arc of a meridian and it describes an arc of a parallel circle (parallel to the equator) when it moves due east. We have to distinguish two cases.
1. 你认为那只熊是白色的，P点是北极？你能证明这一点是正确的吗？正如人们或多或少理解的那样，我们把这个问题理想化。我们把地球看作是完全的球形，而熊是一个移动的物质点。这个点在正南或正北移动时，描述了一条子午线的弧线，在正东移动时，它描述了一个平行圆（与赤道平行）的弧线。我们必须区分两种情况。
(1) If the bear returns to the point P along a meridian different from the one along which he left P, P is necessarily the North Pole. In fact the only other point of the globe in which two meridians meet is the South Pole, but the bear could leave this pole only in moving northward.
（1）如果熊沿着与他离开P 点时 不同的经线返回P点，P 点必然是北极。事实上，地球上唯一一个有两条经线相交的点是南极，但熊只有在向北移动时才能离开这个极点。
(2) The bear could return to the point P along the same meridian he left P if, when walking one mile due east, he describes a parallel circle exactly n times, where n may be 1, 2, 3 . . . In this case P is not the North Pole, but a point on a parallel circle very close to the South Pole (the perimeter of which, expressed in miles, is slightly inferior to 2π + 1/n).
（2）如果在正东方向行走一英里时，熊可以沿着他离开P点的同一子午线返回P点，他正好描述了一个平行圆的n次，其中n可能是 1，2，3 …… 在这种情况下，P不是北极，而是一个非常接近南极的平行圆上的一个点（其周长以英里表示，略逊于 2π+1/n）。
2. We represent the globe as in the solution of Problem 1. The land that Bob wants is bounded by two meridians and two parallel circles. Imagine two fixed meridians, and a parallel circle moving away from the equator: the arc on the moving parallel intercepted by the two fixed meridians is steadily shortened. The center of the land that Bob wants should be on the equator: he can not get it in the U.S.
2. 我们按照问题 1 的解决方案来表示地球。鲍勃想要的土地被两条经线和两个平行圆圈所包围。想象一下，两条固定的经线和一个远离赤道的平行圆：移动的平行线上被两条固定经线截住的弧线不断缩短。鲍勃想要的土地中心应该在赤道上：他在美国是得不到的。
Bob cannot make it: he has only 44 dollars.
鲍勃不能去了：他只有 44 美元。
4. A volume of 999 numbered pages needs
4. 一卷有 999 页编号的书需要
digits. If the bulky volume in question has x pages
数字。如果有关的笨重书册有x页
This problem may teach us that a preliminary estimate of the unknown may be useful (or even necessary, as in the present case).
这个问题可能告诉我们，对未知数的初步估计可能是有用的（甚至是必要的，就像在本案例中）。
5. If _679_ is divisible by 72, it is divisible both by 8 and by 9. If it is divisible by 8, the number 79_ must be divisible by 8 (since 1000 is divisible by 8) and so 79_ must be 792: the last faded digit is 2. If _6792 is divisible by 9, the sum of its digits must be divisible by 9 (the rule about “casting out nines”) and so the first faded digit must be 3. The price of one turkey was (in grandfather’s time) $367.92 ÷ 72 = $5.11.
5. 如果_679_可以被 72 整除，那么它既可以被 8 整除，也可以被 9 整除。如果它可以被 8 整除，那么数字 79_一定可以被 8 整除（因为 1000 可以被 8 整除），所以 79_一定是 792：最后一个消逝的数字是 2。如果_6792 可以被 9 整除，它的数字之和一定可以被 9 整除（关于 “抛出九” 的规则），所以第一个消逝的数字一定是 3。一只火鸡的价格是（在祖父的时代）$367.92÷72=$5.11。
6. “A point and a figure with a center of symmetry (in the same plane) are given in position. Find a straight line that passes through the given point and bisects the area of the given figure.” The required line passes, of course, through the center of symmetry. See INVENTOR’S PARADOX.
6.“给定一个点和一个具有对称中心的图形（在同一平面内）的位置。请找出一条通过给定的点并将给定图形的面积一分为二的直线。” 所要求的直线当然是通过对称中心的。见 “发明家范例”。
7. In any position the two sides of the angle must pass through two vertices of the square. As long as they pass through the same pair of vertices, the angle’s vertex moves along the same arc of circle (by the theorem underlying the hint). Hence each of the two loci required consists of several arcs of circle: of 4 semicircles in the case (a) and of 8 quarter circles in the case (b); see Fig. 31.
7. 在任何位置，角的两边都必须通过正方形的两个顶点。只要它们通过同一对顶点，角的顶点，沿着同一条圆弧移动（根据提示的定理）。因此，所需的两个位置都由几个圆弧组成：（a）情况下由 4 个半圆组成，（b）情况下由 8 个四分之一圆组成；见图 31。
FIG. 31
图 31
8. The axis pierces the surface of the cube in some point which is either a vertex of the cube or lies on an edge or in the interior of a face. If the axis passes through a point of an edge (but not through one of its end-points) this point must be the midpoint: otherwise the edge could not coincide with itself after the rotation. Similarly, an axis piercing the interior of a face must pass through its center. Any axis must, of course, pass through the center of the cube. And so there are three kinds of axes:
8. 轴穿过立方体表面的某一点，要么是立方体的一个顶点，要么位于一条边上，要么位于一个面的内部。如果轴穿过一条边的某一点（但不穿过它的一个端点），这个点必须是中点：否则边在旋转后就不能与自己重合。同样地，穿透一个面的内部的轴必须通过其中心。当然，任何轴都必须通过立方体的中心。因此，有三种轴。
(1) 4 axes, each through two opposite vertices; angles 120°, 240°
（1）4 条轴，每条轴通过两个相对的顶点；角度为 120°，240°。
(3) 3 axes, each through the center of two opposite faces; angles 90°, 180°, 270°.
（3）3 条轴，每条都通过两个相对面的中心；角度为 90°，180°，270°。
For the length of an axis of the first kind see section 12; the others are still easier to compute. The desired average is
关于第一种轴的长度，见第 12 节；其他的还是比较容易计算的。所需的平均数是
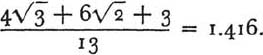
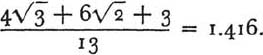
(This problem may be useful in preparing the reader for the study of crystallography. For the reader sufficiently advanced in the integral calculus it may be observed that the average computed is a fairly good approximation to the “average width” of the cube, which is, in fact, 3/2 = 1.5.)
（这个问题对于读者准备学习晶体学可能是有用的。对于在积分计算方面有足够水平的读者来说，可以注意到所计算的平均数是对立方体的 “平均宽度” 的相当好的近似值，实际上是 3/2=1.5）。
9. The plane passing through one edge of length a and the perpendicular of length b divides the tetrahedron into two more accessible congruent tetrahedra, each with base ab/2 and height a/2. Hence the required volume
9. 通过长度为a的一条边和长度为b的垂直线的平面将四面体分成两个更容易接近的全等四面体，每个四面体的底ab/2 和高a/2。因此，所需的体积
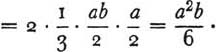
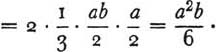
10. The base of the pyramid is a polygon with n sides. In the case (a) the n lateral edges of the pyramid are equal; in the case (b) the altitudes (drawn from the apex) of its n lateral faces are equal. If we draw the altitude of the pyramid and join its foot to the n vertices of the base in the case (a), but to the feet of the altitudes of the n lateral faces in the case (b), we obtain, in both cases, n right triangles of which the altitude (of the pyramid) is a common side: I say that these n right triangles are congruent. In fact the hypotenuse [a lateral edge in the case (a), a lateral altitude in the case (b)] is of the same length in each, according to the definitions laid down in the proposed problem; we have just mentioned that another side (the altitude of the pyramid) and an angle (the right angle) are common to all. In the n congruent triangles the third sides must also be equal; they are drawn from the same point (the foot of the altitude) in the same plane (the base): they form n radii of a circle which is circumscribed about, or inscribed into, the base of the pyramid, in the cases (a) and (b), respectively. [In the case (b) it remains to show, however, that the n radii mentioned are perpendicular to the respective sides of the base; this follows from a well-known theorem of solid geometry on projections.]
10. 金字塔的底部是一个有n条边的多边形。在（a）情况下，金字塔的n 个侧边是相等的；在（b）情况下，其n 个侧边的高度（从顶点开始画）是相等的。如果我们画出金字塔的高度，在（a）的情况下，将它的脚与底座的n 个顶点相连，而在（b）的情况下，将它的脚与n 个侧边的高度相连，在这两种情况下，我们得到n 个直角三角形，其中（金字塔的）高度 是一个公共边：我说这n 个直角三角形是全等的。事实上，根据拟议问题中的定义，每个三角形的斜边（a）中的侧边，（b）中的侧边高度长度相同；我们刚刚提到，另一条边（金字塔的高度）和一个角（直角）都是共同的。在n 个全等三角形中，第三条边也必须相等；它们从同一平面（底面）的同一点（高度的脚）出发：在（a）和（b）的情况下，它们分别构成一个圆的n 个半径，这个圆是围绕金字塔底面的，或者说是刻在金字塔底面的。[然而，在（b）的情况下，仍然需要证明，所述的n 个半径与基底的各边垂直；这是由关于投影的一个著名的实体几何定理得出的。］
It is most remarkable that a plane figure, the isosceles triangle, may have two different analogues in solid geometry.
最引人注目的是，一个平面图形，即等腰三角形，在实体几何中可能有两个不同的类似物。
11. Observe that the first equation is so related to the last as the second is to the third: the coefficients on the left-hand sides are the same, but in opposite order, whereas the right-hand sides are opposite. Add the first equation to the last and the second to the third:
11. 请注意，第一个方程与最后一个方程的关系就像第二个方程与第三个方程的关系一样：左手边的系数相同，但顺序相反，而右手边的系数则相反。将第一个方程加入最后一个方程，第二个方程加入第三个方程。
This can be regarded as a system of two linear equations for two unknowns, namely for x + u and y + v, and easily yields
这可以看作是两个未知数的两个线性方程组，即x+u和y+v，并且很容易得到
Substituting −x for u and −y for v in the first two equations of the original system, we find
在原系统的前两个方程中用-x代替u，用-y代替v，我们发现
This is a simple system which yields
这是一个简单的系统，其结果是
Bob traveled as much as Paul:
鲍勃和保罗一样都在旅行。
Paul traveled as much as Peter:
保罗和彼得一样都在旅行。
The second equation yields
第二个方程的结果是
We assume, of course, that the car travels faster than a pedestrian, c > p. It follows
当然，我们假设汽车的速度比行人快，c>p。
that is, Peter walks just as much as Paul. From the first equation, we find that
也就是说，彼得和保罗走的路一样多。从第一个等式中，我们发现
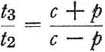
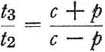
which is, of course, also the value for t1/t2. Hence we obtain the answers:
当然，这也是t1/t2的值。因此，我们得到了答案。
(a)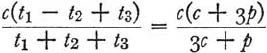 
（a）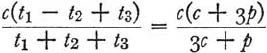
(b) 
（b）
(c) In fact, 0 < p < c. There are two extreme cases:
（c）事实上，0 <p<c. 有两种极端情况。
If p = 0 (a) yields c/3 and (b) yields 1/3
如果p=0，（a）得到c/3，（b）得到 1/3
If p = c (a) yields c and (b) yields 0.
如果p=c（a）得到c，（b）得到 0。
These results are easy to see without computation.
这些结果不用计算就很容易看到。
The last equation yields a = 42, then the second b = 34. Adding the remaining two equations (to eliminate d), we obtain
最后一个方程得出a=42，然后第二个b=34。将剩下的两个方程相加（消除d），我们得到
Since a and b are already known, we have here a quadratic equation for g. It yields
由于a和b已经知道，我们这里有一个g的二次方程。
The progressions are
进展情况是
14. If a and −a are the roots having the least absolute value, they will stand next to each other in the progression which will, therefore, be of the form
14. 如果a和-a是具有最小绝对值的根，它们将在级数中相邻而立，因此，级数的形式将是
Hence the left-hand side of the proposed equation must have the form
因此，拟议方程的左手边必须具有以下形式
Carrying out the multiplication and comparing coefficients of like powers, we obtain the system
进行乘法运算并比较同类幂的系数，我们得到系统
Hence m = 6 or −6/19.
因此，m=6 或-6/19。
15. Let a, b, and c denote the sides, the last being the hypotenuse. The three parts of the condition are expressed by
15. 让a、b、c表示边，最后一条是斜边。该条件的三个部分用以下方式表示
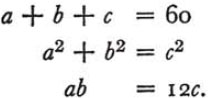
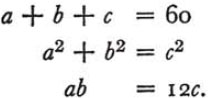
Observing that
观察到
we obtain
我们得到
Hence c = 25 and either a = 15, b = 20 or a = 20, b = 15 (no difference for the triangle).
因此，c=25，要么a=15，b=20，要么a=20，b=15（对三角形来说没有区别）。
16. The three parts of the condition are expressed by
16. 该条件的三个部分用以下方式表示
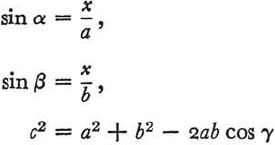
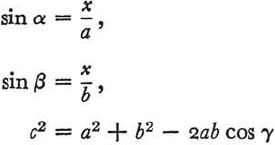
The elimination of a and b yields
消除a和b后，得到
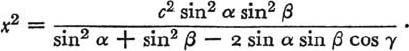
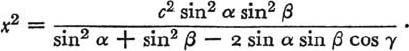
17. We conjecture that
17. 我们猜测
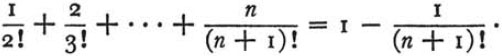
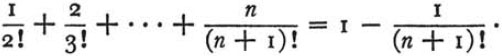
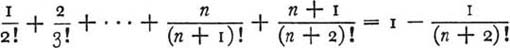
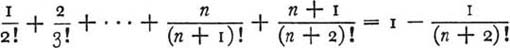
Check this by subtracting from it the former:
通过从中减去前者来检查这一点。
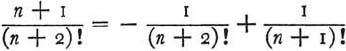
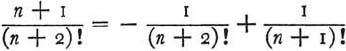
which boils down to
归纳起来就是
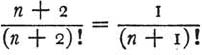
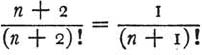
and this last equation is obviously true for n = 1, 2, 3, . . . hence, by following the pattern referred to above, we can prove our conjecture.
最后一个方程对于n=1、2、3、…… 显然是真实的，因此，通过遵循上面提到的模式，我们可以证明我们的猜想。
18. In the nth line the right-hand side seems to be n3 and the left-hand side a sum of n terms. The final term of this sum is the mth odd number, or 2m − 1, where
18. 在第n行中，右手边似乎是n3，左手边是n项之和。这个和的最后一项是第m个奇数，或2m- 1，其中
see INDUCTION AND MATHEMATICAL INDUCTION, 4. Hence the final term of the sum on the left-hand side should be
因此，左手边的和的最后一项应该是
We can derive hence the initial term of the sum considered in two ways: going back n − 1 steps from the final term, we find
因此，我们可以通过两种方式推导出所考虑的和的初始项：从最后一项往回走n- 1 步，我们发现
whereas, advancing one step from the final term of the foregoing line, we find
而从前述线条的最后一项向前推进一步，我们发现
where the left-hand side indicates the sum of n successive terms of an arithmetic progression the difference of which is 2. If the reader knows the rule for the sum of such a progression (arithmetic mean of the initial term and the final term, multiplied by the number of terms), he can verify that
如果读者知道这种级数之和的规则（初始项和最后项的算术平均数，乘以项数），他可以证明
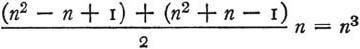
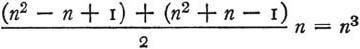
and so prove the assertion.
并因此证明了这一论断。
(The rule quoted can be easily proved by a picture little different from Fig. 18.)
（所引用的规则可以通过与图 18稍有不同的图片轻松证明）。
19. The length of the perimeter of the regular hexagon with side n is 6n. Therefore, this perimeter consists of 6n boundary lines of length 1 and contains 6n vertices. Therefore, in the transition from n − 1 to n, V increases by 6n units, and so
19. 边长为n的正六边形的周长为6n。因此，这个周长由6n条长度为 1 的边界线组成，包含6n 个顶点。因此，在从n-1 到n的过渡中，V增加了6n个单位，所以
see INDUCTION AND MATHEMATICAL INDUCTION, 4. By 3 diagonals through its center the hexagon is divided into 6 (large) equilateral triangles. By inspection of one of these
通过 3 条穿过中心的对角线，六边形被分成 6 个（大）等边三角形。通过对其中一个的检查
(rule for the sum of an arithmetic progression, quoted in the solution of Problem 18). The T triangles have jointly 3T sides. In this total 3T each internal line of division of length 1 is counted twice, whereas the 6n lines along the perimeter of the hexagon are counted but once. Hence
（问题 18 的解答中引用了算术级数之和的规则）。T个三角形共同拥有3T条边。在这个总数为3T的三角形中，每条长度为 1 的内部分割线被计算两次，而沿六边形周长的6n条线只被计算一次。因此
20. Here is a well-ordered array of analogous problems: Compute An, Bn, Cn, Dn and En. Each of these quantities represents the number of ways to pay the amount of n cents; the difference is in the coins used:
20. 这里有一个排列有序的类似问题。计算An、Bn、Cn、Dn和En。这些数量中的每一个都代表了支付n美分金额的方法的数量；区别在于使用的硬币。
An only cents
一个唯一的美分
Bn cents and nickels
美分和镍币
Cn cents, nickels, and dimes
Cn美分、五分和一角硬币
Dn cents, nickels, dimes, and quarters
美分、五角、一角和五角硬币
En cents, nickels, dimes, quarters, and half dollars.
恩美分、五分钱、一角钱、五角钱和半美元。
The symbols En (reason now clear) and An were used before.
之前使用的是符号En（原因现在清楚了）和An。
All ways and manners to pay the amount of n cents with the five kinds of coin are enumerated by En. We may, however, distinguish two possibilities:
恩列举了用五种硬币支付n美分的所有方法和方式。然而，我们可以区分两种可能性。
First. No half dollar is used. The number of such ways to pay is Dn, by definition.
首先。没有使用半元。根据定义，这种支付方式的数量为Dn。
Second. A half dollar (possibly more) is used. After the first half dollar is laid on the counter, there remains the amount of n − 50 cents to pay, which can be done in exactly En−50 ways.
第二。用的是半美元（可能更多）。第一块半美元放在柜台上后，还剩下n-50 美分的金额需要支付，这正好可以用En-50的方式来完成。
We infer that
我们推断，
Similarly
同样地
A little attention shows that these formulas remain valid if we set
稍微注意一下就会发现，如果我们把这些公式设为
Our formulas allow us to compute the quantities considered recursively, that is, by going back to lower values of n or to former letters of the alphabet. For example, we can compute C30 by simple addition if C20 and B30 are already known. In the table below the initial row, headed by An, and the initial column, headed by 0, contain only numbers equal to 1. (Why?) Starting from these initial numbers, we compute the others recursively, by simple additions: any other number of the table is equal either to the number above it or to the sum of two numbers: the number above it and another at the proper distance to the left. For example,
我们的公式允许我们递归地计算所考虑的数量，也就是说，通过回溯到n的低值或字母表的前几个字母。例如，如果C20和B30已经知道，我们可以通过简单的加法计算C30。在下面的表格中，以An为首的初始行和以 0 为首的初始列只包含等于 1 的数字。（为什么？）从这些初始数字开始，我们通过简单的加法递归地计算其他的数字：表中的任何其他数字要么等于它上面的数字，要么等于两个数字的总和：它上面的数字和左边适当距离的另一个。比如说
The computation is carried through till E50 = 50: you can pay 50 cents in exactly 50 different ways. Carrying it further, the reader can convince himself that E100 = 292: you can change a dollar in 292 different ways.
这个计算一直进行到E50=50：你可以 用正好50 种不同的方式 支付50美分。再继续下去，读者可以说服自己，E100=292：你可以用292 种不同的方式 换取一美元。
12 Except Problem 1 (widely known, but too amusing to miss) all the problems are taken from the Stanford University Competitive Examinations in Mathematics (there are a few minor changes). Some of the problems were formerly published in The American Mathematical Monthly and/or The California Mathematics Council Bulletin. In the latter periodical also some solutions were published by the author; they appear appropriately rearranged in the sequel.
12除了问题 1（广为人知，但太有趣了，不能错过），所有的问题都来自斯坦福大学的数学竞赛考试（有一些小改动）。其中一些问题曾发表在《美国数学月刊》和/或《加利福尼亚数学委员会公报》上。在后者的期刊中，作者也发表了一些解决方案；它们在续集中被适当地重新排列。
